Влияние ошибок наблюдений на статистические параметры и функции

Ограниченность объема выборки является не единственным фактором, вносящим погрешности в рассчитываемые ковариационные или корреляционные функции. Значительные искажения могут возникнуть и при наличии ошибок наблюдения.

Пусть при измерении величины в точке имеет место некоторая ошибка , тогда получим величину

. (97)

Ошибка состоит из систематической и случайной составляющей

. (98)

Из равенства (97) и (98) следует, что

, (99)

здесь .

Таким образом, при оценивании средней величины ее значение изменяется только на величину систематической ошибки. При вычислении дисперсии величины влияние оказывают также случайные ошибки наблюдений. Действительно, учитывая (97)-(99)

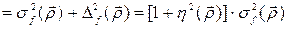, (100)

где —дисперсия ошибок наблюдения, а

—

— мера ошибок наблюдения. Формула получена при условии, что связь между случайной ошибкой и функцией отсутствует, т.е. .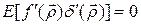

Формула (100) показывает, что на дисперсию систематические ошибки не оказывают влияния, но она завышается на величину дисперсии случайной ошибки.

При оценивании ковариационных функций, определяемых по данным, содержащим ошибки, используется следующая формула

. (101)

Как следует из (101) значение ковариационной функции также не искажается наличием систематической ошибки, но существенно зависит от коррелированности ошибок в различных точках и от взаимной коррелированности ошибок и значений самой величины .

Будем в дальнейшем рассматривать только случайные ошибки наблюдений. Случайными ошибками называются такие, которые удовлетворяют следующим условиям.

1. Средняя величина случайной ошибки равна нулю.

. (102)

2. Корреляция случайных ошибок в различных точках отсутствует.

,

где

символ Кронекера

3. Случайные ошибки не коррелируют со значениями самого метеоэлемента.

. (103)

Если принять во внимание все эти условия, то (101) примет вид

. (104)

Из (104) следует, что наличие ошибок в исходных данных не влияет на ковариацию случайной величины в различных точках. Нетрудно видеть также, что при i=j формула (104) переходит в формулу (100).

Для значений эмпирических структурных функций получается следующее выражение

. (105)

В случае, если поле является однородным и изотропным, то предполагается, что

,

. (106)

При этом формула (105) примет вид

(107)

Если расстояние между точками равно нулю, то из (107) получим

(108)

На этом равенстве основан один из способов определения дисперсии случайных ошибок в данных. Для этого рассчитывают значения структурной функции при расстояниях между точками . Полученные значения можно нанести на график, т. е. построить зависимость . Затем проводят экстраполяцию (обычно ли­нейную) структурной функции в точку . Значение структур­ной функции при представляет удвоенную дисперсию ошибок наблюдения.

Остановимся теперь на влиянии случайных ошибок на значения корреляционных функций. В отличие от ковариационных функций, на значения которых случайные ошибки не влияют при i ≠j (см. формулу (104)), значения корреляционных функций под влиянием случайных ошибок занижаются. Это видно из следующего равенства

. (109)

В случае однородных и изотропных полей формула (109) принимает вид

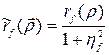(110)

Как следует из формулы (110), при стремлении расстояния ρ к нулю корреляционная функция, стремится не к 1, а к величине

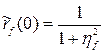(111)

Используя формулу (111), можно оценить точность исходных данных, если проэкстраполировать значение эмпирической корреляционной функции в точку . В этом случае из (111) получим

. (112)