При обработке и анализе реальных метеорологических полей существенные погрешности могут возникать из-за того, что временные ряды не являются стационарными. Нестационарность может вызываться, например, изменением во времени средних величин и дисперсий. Еще более сложную структуру имеют процессы, у которых во времени изменяются ковариационные функции и спектральные плотности.
Рассмотрим наиболее простой, пример, когда значение случайной метеовеличины искажено влиянием годового хода.
(113)
Функция Q (ρ, t) описывает годовой ход.
Выполним статистическое осреднение (113) по некоторому участку годового хода
. (114)
Вычитая (114) из (113), будем иметь
, (115)
где
(116)
Из (116), в частности, следует, что
.
Для автоковариационной функции случайной величины можно записать следующее выражение
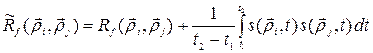(117)
Для того чтобы оценить влияние последнего слагаемого в (117), зададим годовой ход в виде ряда Фурье
. (118)
Ограничившись первой гармоникой и подставляя (118) при п = 1в (116) и (116) в (117), получим следующее выражение для ковариационной функции
. (119)
Это выражение получено в предположении, что амплитуда колебаний в точках i и j одинакова, и фазы колебаний также совпадают. В формуле (119) множитель K (t2, t1)имеет вид
(120)
Величина 
- называется мерой нестационарности для периода времени Т. Используя это обозначение, можно записать (119) в следующем виде:
(121)
Формулы (120|) и (121) позволяют количественно оценить влияние нестационарности, вызванной годовым ходом, на величину ковариационной функции. Количественные оценки приведены в табл. 11.
Из таблицы видно, что влияние нестационарное оказывается существенным в ряде случаев. Завышение происходит на величину пропорциональную квадрату годовой амплитуды.
|
|
Для того чтобы исключить влияние нестационарности, обычно проводят некоторые дополнительные преобразования временных рядов. Например, если нестационарность обусловлена изменением во времени средней величины и дисперсии, то обычно вместо наблюдаемой величины y(t) рассматривают следующую величину:
Таблица 11
Завышение ковариации К под влиянием годового хода
| Период времени | Дата | K |
| Год | - | 0,500 |
| Полугодия: | ||
| экстремальное | 15.IV— 15.X, 15.X—15.IV | 0,095 |
| промежуточное | 0l.III—01.IX, 01.VI—01.ХП 01. IX—01.Ш, 01.XII—0l.VI | 0,294 |
| переходное | 15.I—15.VII, 15.VII—15.I | 0,500 |
| Сезон: | ||
| экстремальный | 01.VI—1.IX, 01.XII—1.III 15. IV—15.VII, 15.VII—15.Х | 0,008 |
| промежуточный | 15.X—15.Ш, 15.l—l5.IV | 0,094 |
| переходный | 01.1Х—l.XII, 01.III—1.Vl | 0,182 |
Полученная реализация случайного процесса, который считается приближенно стационарным, обрабатывается при помощи численных схем, описанных выше.
Рассмотрим влияние ошибки, не связанной с влиянием годового хода.
Пусть при измерении величины 
в точке 
имеет место некоторая ошибка, связанная с нестационарностью 
, тогда получим величину
. (122)
Из равенства (122) следует, что
, (123)
здесь 
среднее значение ошибки, вызванной нестационарностью.
Таким образом, при оценивании средней величины ее значение изменяется только на величину средней ошибки нестационарности.
При вычислении дисперсии величины 
ошибка нестационарности также оказывает влияние
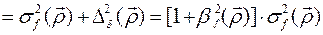, (124)
где 
—дисперсия ошибок нестационарности, а
— мера ошибки нестационарности.
Формула получена при условии, что связь между ошибкой нестационарности и функцией отсутствует, т.е.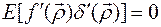 
.
|
|
Формула (124) показывает, что дисперсия завышается на величину дисперсии ошибки нестационарности.
Оценивание ковариационной функции с учетом ошибки нестационарности при условии однородности и изотропии
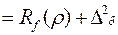. (125)
Как следует из (125) значение ковариационной функции завышается за счет дисперсии ошибки нестационарности.
Влияние ошибки нестационарности на величину корреляционной функции можно оценить, учитывая ее связь с ковариационной функцией
(126)
Таким образом, за счет ошибки нестационарности завышается значение дисперсии, ковариационной и корреляционной функций, последняя искажается в наименьшей степени. На величину структурной функции нестационарность такого рода не сказывается.