Что называется формой потери устойчивости стержня?
При потере устойчивости прямолинейная ось стержня искривляется. Конфигурация изогнутой оси стержня называется формой потери устойчивости. Форма потери устойчивости зависит от условий закрепления стержня и места приложения сжимающей нагрузки по его длине.
Какая нагрузка называется эйлеровой?
В 1744 г. Леонард Эйлер (1707 – 1783 гг.) впервые получил формулу для определения теоретической нагрузки, при которой происходит потеря устойчивости стержня. Эту нагрузку, как правило, называют эйлеровой. Она равна:
, (12.1)
где Е – модуль Юнга; 
– минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости); 
– коэффициент приведения длины, зависящий от формы потери устойчивости (не путайте его с коэффициентом Пуассона); l – длина стержня. Произведение 
называется приведенной, или свободной, длиной стержня.
Почему коэффициентназываетсякоэффициентом приведения длины, а произведение –приведенной длиной стержня?
Для шарнирно опертого стержня, сжатого по концам, Эйлером была получена следующая формула
.
В этом случае 
. Форма потери устойчивости такого стержня представляет собой одну полуволну синусоиды (рис. 12.2, а).И этот случай принято считать основным случаем потери устойчивости.
Н 
екоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по его торцам) легко могут быть приведены к основному случаю путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.
Рассмотрим еще два наиболее часто встречающихся случая закрепления концов стержня.
|
|
2. Стержень с жестко защемленным одним и совершенно свободным другим концом. При потере устойчивости он изогнется, как показано на (рис. 12.2, б). Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Следовательно, в этом случае, приведенная длина равна 
(полуволна синусоиды имеет длину ), а эйлерова сила в четыре раза меньше, чем для основного случая:
.
3. Оба конца стержня жестко защемлены. В этом случае форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 12.2, в). Поэтому приведенная длина стержня равна 
(
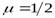), а эйлерова нагрузка
,
то есть в четыре раза больше, чем для основного случая.
Всегда ли справедлива формула Эйлера? Иными словами, всегда ли значение эйлеровой нагрузки совпадает со значением критической нагрузки?
Отметим, что критической 
принято называть истинную, а эйлеровой 
– теоретическую нагрузку, при которой происходит потеря устойчивости стержня.
Формула Эйлера получена при предположении, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности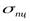 
, то есть
. (12.2)
Об этом, в частности, говорит присутствие в формуле (12.1) модуля ЮнгаЕ, который свидетельствует о том, чтовплоть до момента потери устойчивости выполнялся закон Гука.
Поэтому, если потеря устойчивости происходит при напряжении меньшем, чем 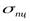, то 
.
Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности 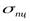, использование формулы Эйлера не только принципиально неправильно, но и крайне опасно по своим последствиям, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой: 
.
|
|