Статистическое распределение выборки

Тема 2.1. Выборки и их характеристики

1. Предмет и задачи математической статистики.

2. Генеральная и выборочная совокупности.

3. Статистическое распределение выборки.

4. Эмпирическая функция распределения.

5. Графическое изображение статистического распределения.

6. Числовые характеристики статистического распределения.

7. Корреляционный анализ выборочной совокупности (оценка выборочного корреляционного момента системы двух случайных величин; регрессионный анализ двух случайных величин).

Математическая статистика является частью общей при­кладной математической дисциплины “Теория вероятностей и математическая статистика”, однако задачи, решаемые ею, но­сят специфический характер. Если теория вероятностей иссле­дует Явления, полностью заданные их моделью, то в математи­ческой статистике вероятностная модель определена с точно­стью до неизвестных параметров. Отсутствие сведений о па­раметрах компенсируется “пробными” испытаниями, на основе которых и восстанавливается недостающая информация. Цель математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Первой задачей математической статистики является ука­зание методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюде­ний.

Вторая задача — это разработка методов анализа стати­стических данных: оценки неизвестных вероятности события, а также функции и параметров распределения; оценка зависи­мости случайной величины от других случайных величин; про­верка статистических гипотез о виде и величинах параметров неизвестного распределения. Рассмотрим некоторые из этих вопросов.

Выборки

На практике сплошное исследование (каждого объекта из интересующей нас совокупности) проводят крайне редко. К то­му же если эта совокупность содержит большое число объек­тов или исследование объекта требует нарушения его функци­онального стандарта, то сплошное исследование нереально. В таких случаях из всей совокупности случайно отбирают огра­ниченное число объектов и подвергают их исследованию.

Введем основные понятия, связанные с выборками.

Ге­неральной совокупностью называется совокупность объектов, из которых производится выборка.

Выборочной совокупно­стью (выборкой) называется совокупность случайно отобран­ных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом.

Пример 1. Пусть из 2000 изделий отобрано для обследования 100 изделий. Тогда объем генеральной совокупности N = 2000, а объем выборки п = 100.

Выборку можно осуществлять двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то вы­борка называется бесповторной.

Выборка называется репрезентативной (представитель­ной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности.

Способы отбора

Различают два способа отбора: без расчленения генераль­ной совокупности на части и с расчленением.

К первому отно­сятся простые случайные отборы (либо повторный, либо бесповторный), когда объекты извлекают по одному из всей гене­ральной совокупности; такой отбор можно производить с ис­пользованием таблицы случайных чисел.

Второй способ отбора включает следующие разновидности, соответствующие способам расчленения генеральной совокуп­ности.

Отбор, при котором объекты отбираются из каждой “ти­пической ” части генеральной совокупности, называется типи­ческим. Например, отбор деталей из продукции каждого стан­ка, а не из их общего количества является типическим.

Если генеральную совокупность делят на число групп, равное объ­ему выборки, с последующим отбором из каждой группы по одному объекту, то такой отбор называется механическим.

Се­рийным называется отбор, при котором объекты отбираются не по одному, а сериями; этот способ используется, когда исследу­емый признак имеет незначительные колебания в различных сериях.

На практике часто употребляется комбинирование указан­ных выше способов отбора. Например, генеральную совокуп­ность разбивают на серии одинакового объема, затем случай­ным образом отбирают несколько серий и в завершение слу­чайным извлечением отдельных объектов составляют выборку. Конкретная комбинация способов отбора объектов из генераль­ной совокупности определяется требованием репрезентативно­сти выборки.

Таким образом на выборку будем смотреть как на совокупность независимых случайных величин x₁, x ₂,..., x _n, распределенных так же, как и случайная величина x, представляющая генеральную совокупность. Выборочные значения x ₁, x ₂,..., x_n – это значения, которые приняли эти случайные величины в результате 1-го, 2-го,..., n -го эксперимента.

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка объема п, в которой значение х₁ некоторого исследуемого признака X наблюдалось n₁ раз, значение х₂ – n₂ раз,..., зна­чение х_к – n_k раз. Значения x_i называются вариантами, а их последовательность, записанная в возрастающем порядке, — вариационным рядом. Числа n_i называются частотами, а их отношения к объему выборки

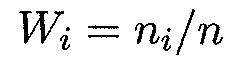(15.47) — относительными частотами. При этом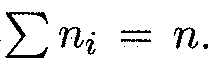

Если промежуток между наименьшим и наибольшим значениями признака в выборке разбить на несколько интервалов одинаковой длины, каждому интервалу поставить в соответствие число выборочных значений признака, попавших в этот интервал, то получим интервальный вариационный ряд. Если признак может принимать любые значения из некоторого промежутка, то есть является непрерывной случайной величиной, приходится выборку представлять именно таким рядом. Если в вариационном интервальном ряду каждый интервал [a _i;a _{i+ 1}) заменить лежащим в его середине числом (a _i +a _{i+ 1})/2, то получим дискретный вариационный ряд. Такая замена вполне естественна, так как, например, при измерении размера детали с точностью до одного миллиметра всем размерам из промежутка [49,5; 50,5), будет соответствовать одно число, равное 50.

Модой М₀ называется варианта, имеющая наибольшую частоту.

Ме­дианой т_е называется варианта, которая делит вариационный ряд на две части с одинаковым числом вариант в каждой. Ес­ли число вариант нечетно, т.е. 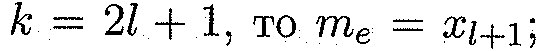если же число вариант четно (к = 2l), то .

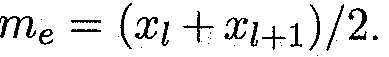Разма­хом варьирования называется разность между максимальной и минимальной вариантами или длина интервала, которому при­надлежат все варианты выборки:

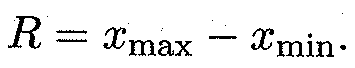(15.48)

Перечень вариант и соответствующих им частот называ­ется статистическим распределением выборки. Здесь имеет­ся аналогия с законом распределения случайной величины: в теории вероятностей — это соответствие между возможными значениями случайной величины и их вероятностями, а в ма­тематической статистике — это соответствие между наблюда­емыми вариантами и их частотами (относительными частота­ми). Нетрудно видеть, что сумма относительных частот равна единице: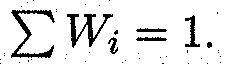

Пример 2. Выборка задана в виде распределения частот:

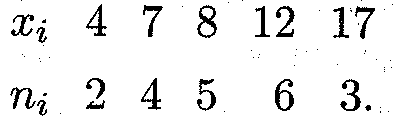
Найти распределение относительных частот и основные харак­теристики вариационного ряда.

Решение. Найдем объем выборки: п = 2+4+5+6+3 = 20. Относительные частоты соответственно равны W₁ = 2/20 = = 0,1; W₂ = 4/20 = 0,2; W₃ = 5/20 = 0,25; W₄ = 6/20 = 0,3; W₅ = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид

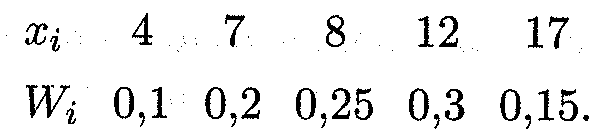
Мода этого вариационного ряда равна 12. Число вариант н данном случае нечетно: k = 2*2 + 1, поэтому медиана т_е = x_{3 =} 8.

Размах варьирования, согласно формуле (15.48), R = 17-4 = 13.