Равномерное распределение вероятностей
- Случайная величина
задана интегральной функцией, график которой представлен на рисунке.
Найдите плотность вероятности и по виду функции определите, какое распределение вероятностей имеет эта случайная величина.
2. Закон равномерного распределения вероятностей случайной величины задан плотностью вероятности:
Найдите интегральную функцию случайной величины .
3. Случайная величина имеет равномерное распределение вероятностей на интервале (4; 10). Найдите ее математическое ожидание, дисперсию и среднее квадратическое отклонение.
4. Случайная величина имеет равномерное распределение вероятностей. Найдите плотность вероятности, если математическое ожидание случайной величины равно 8, а дисперсия равна 
.
5. Из фиксированной вершины квадрата со стороной 
произвольным радиусом, меньшим его диагонали, проведена окружность. Какова вероятность того, что она пересечет стороны квадрата, которым принадлежит данная вершина?
6. Два действительных числа 
и 
выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность того, что сумма этих квадратов окажется больше 64?
7. В течение 20 минут после девяти часов ученик А в случайный момент времени звонит по телефону ученику В, ждет 2 минуты, после чего кладет трубку. В течение тех же 20 минут ученик В заходит в свою квартиру в случайный момент и остается дома в течение 4 минут. Какова вероятность того, что разговор между учениками состоится?
8. В равносторонний треугольник, сторона которого равна , вписан круг. Внутри треугольника независимо друг от друга наудачу выбираются 5 точек. Какова вероятность того, что 3 из этих точек окажутся внутри круга?
9. Внутри шара радиуса 
некоторым способом наудачу выбирается точка. Необходимо найти интегральную и дифференциальную функции распределения случайной величины , выражающей расстояние от точки до центра шара.
Нормальное распределение вероятностей
1. Плотность вероятности случайной величины , подчиненной нормальному закону распределения, задана функцией
.
Найдите коэффициент 
и определите вероятность того, что в результате испытания случайная величина примет значение в интервале (2; 5).
2. Во сколько раз уменьшится максимальное значение ординаты нормальной кривой, если дисперсия случайной величины увеличится в 9 раз?
3. Максимальное значение плотности вероятности случайной величины , подчиненной нормальному закону распределения равно 
. Найдите среднее квадратическое отклонение и дисперсию этой случайной величины.
4. Случайная величина распределена нормально и имеет плотность вероятности
.
Найдите математическое ожидание случайной величины 
(также подчиненной нормальному закону распределения вероятностей).
5. Случайная величина имеет плотность вероятности
.
Найдите вероятность того, что случайная величина примет значение в интервале (4; 6).
6. Случайная величина подчинена нормальному закону распределения с математическим ожиданием 
. Определите дисперсию случайной величины , если известно, что вероятность принятия случайной величиной значения в интервале (50; 60) равна 0,3413.
7. Случайная величина подчинена нормальному закону распределения с параметрам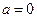и 
и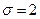 
. Найдите интервал 
, в котором эта случайная величина принимает свои возможные значения с вероятностью 0,61, если известно, что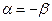 
.
8. При измерении детали ее длина является случайной величиной, распределенной по нормальному закону с параметрами 
см и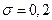 
см. Найдите интервал, в который с вероятностью 0,9544 попадет .