Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Тульский государственный университет»
ИПМКН
Кафедра ВММ
| Утверждаю Зав каф ВММ __________________ (В.В.Глаголев ) “____”_________________ 2018 г. |
ТЕСТЫ
ДЛЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
по дисциплине
Дискретная математика
Направление подготовки: 090900 Информационная безопасность
Профиль подготовки: организация и технология защиты информации
Квалификация: 62 “бакалавр”
Форма обучения:для всех форм
Тула 2018 г.
Разработал: В.В. Козлов, канд. физ.-мат. наук, ассистент
«Теория множеств»
1. Дано множество 
. Какие из утверждений верны:
а) 
;
б) 
;
в) 
;
г) 
.
2. Определить мощность множества 
:
а) 
;
б) 
;
в) 
;
г) 
.
3. Выбрать верный вариант формулы для определения мощности булеана В(А):
а) 
;
б) 
;
в)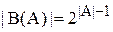 
;
г)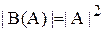 
.
4. Определить мощность булеана множества А={{a, b}, c}:
а) 
;
б) 
;
в)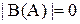 
;
г) 
.
5. Выбрать верный порядок убывания старшинства операций алгебры Кантора:
а) 
;
б) 
;
в) 
;
г) 
.
6. Какая формула соответствует дистрибутивному закону:
а) 
;
б) 
;
в) 
;
г) 
.
7. Указать формулу, соответствующую закону Порецкого:
а) ;
б) ;
в) ;
г) .
8. Могут ли повторяться элементы множества?
а) да;
б) нет.
9. Является ли множество несобственным подмножеством самого себя?
а) да;
б) нет.
10. Множества равны, если они содержат:
а) одни и те же элементы;
б) одинаковое количество элементов.
11. Являются ли понятия мощности множества и его кардинального числа идентичными?
а) да;
б) нет.
12. Булеан множества А={{1, 2}, 3} определяется как:
а) 
;
б) 
;
в)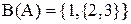 
;
г) 
.
13. Какое из утверждений верно для всех множеств А, В, С:
а) если 
и 
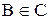, то 
;
б) если 
и 
, то 
;
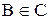в) если и , то ;
г) ни одно не верно.
14. Какой закон определяется формулой 
?
а) элиминации;
б) Порецкого;
в) Де Моргана;
г) инволюции.
15. Чему равно выражение 
:
а) 
;
б) 
;
в) 
;
г) 
.
16. Могут ли повторяться компоненты вектора?
а) да;
б) нет.
17. Длина вектора определяется:
а) числом различных элементов;
б) числом координат.
18. Верно ли: 
?
а) да;
б) нет.
19. Какое из соответствий называется взаимно-однозначным:
а) сюръективное, инъективное и функциональное?
б) сюръективное и инъективное?
в) всюду определенное, сюръективное, инъективное и функциональное?
20. Является ли отображение биективным, если оно сюръективно и инъективно?
а) да;
б) нет.
21. Отображение А в В это:
а) частично определенная функция;
б) всюду определенная функция;
в) сюръективное соответствие;
г) инъективное соответствие.
22. Указать определение инъективного соответствия 
а) 
;
б) 
;
в) 
;
г) 
.
23. Какая из формул не задает функцию:
а) 
;
б) 
;
в) 
;
г) 
.
24. Проекция соответствия 
на первую ось равна
а) 
б) 
в)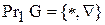 
г) 
25. Проекция соответствия на вторую ось равна
а)
б)
в)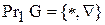
г) 
26. Указать проекцию множества A={(3,3,5), (3,3,6), (3,5,5), (3,5,6), (8,3,5), (8,3,6), (8,5,5), (8,5,6)} на третью ось
а) PrA={3,8},
б) PrA={3,5},
в) PrA={5,6}.
27. Верно ли: |Аn| = |A|n?
а) да
б) нет.
28. Отношением степени n называется:
а) произвольное подмножество данного множества;
б) подмножество декартова произведения двух множеств;
в) подмножество декартова произведения любого конечного
количества множеств;
г) подмножество декартовой степени множества;
д) результат объединения данных множеств;
е) результат пересечения данных множеств.
29. В каком случае 
и 
являются совместимыми?
а) 
;
б) 
;
в)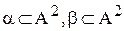 
.
30. Для каких из операций над отношениями выполнение условия совместимости является не обязательным:
а) 
;
б)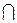 
;
в) \;
г) 
.
31. Отношения являются совместимыми:
а) всегда;
б) если они имеют разные степени;
в) если они имеют одинаковые степени;
г) если они бинарные.
32. Какие из операций реляционной алгебры применимы к отношениям 
:
а) 
;
б) 
;
в) \;
г) .
д) все;
е) ни одна не применима.
33. Какие из операций реляционной алгебры применимы к отношениям :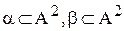
а) ;
б) ;
в) \;
г) ;
д) все;
е) ни одна не применима.
34. Операция выбора представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) «бинарного» подмножества отношения;
35. Операция проекции представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения.
36. Операция проекции по двум доменам представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) бинарного подмножества отношения.
37. Операция проекции по одному домену представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) бинарного подмножества отношения;
д) некоторого отношения степени n;
е) множества элементов, не являющегося отношением.
38. Какое из отношений является бинарным:
а)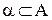 
;
б) 
;
в)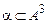 
.
39. Если матрица, описывающая бинарное отношение, содержит на главной диагонали и нули и единицы, то отношение:
а) рефлексивно;
б) антирефлексивно;
в) не рефлексивно.
40. Если все вершины графа, описывающего отношение, имеют петли, то отношение:
а) рефлексивно;
б) антирефлексивно;
в) не рефлексивно.
41. Если в графе, описывающем отношение, имеется хотя бы одна пара вершин, соединенных одной дугой, является ли данное отношение симметричным?
а) да;
б) нет.
42. Классы эквивалентности:
а) попарно пересекаются;
б) попарно не пересекаются.
43. Верно ли, что любые два элемента из одного класса эквивалентности эквивалентны?
а) да;
б) нет.
44. Верно ли, что любые два элемента из разных классов эквивалентности не эквивалентны?
а) да;
б) нет.
45. Если отношение антирефлексивно, антисимметрично и транзитивно, оно является:
а) отношением нестрогого порядка;
б) отношением строгого порядка;
в) не является отношением порядка.
46. Если любые два элемента множества M, на котором задано отношение порядка, сравнимы, М является:
а) неупорядоченным;
б) линейно упорядоченным;
в) частично упорядоченным;
47. Среди следующих отношений, заданных на множестве отрезков, укажите отношение порядка:
а) отрезок х равен отрезку у;
б) отрезок х короче отрезка у в 2 раза;
в) отрезок х длиннее отрезка у.
48. Дано множество 
. Какие из утверждений верны:
а)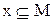 
;
б) 
;
в)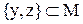 
;
г) 
.
49. Определить мощность множества 
:
а) 
;
б) 
;
в) 
;
г)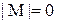 
.
50. Определить мощность булеана множества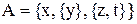 
:
а) 
;
б) 
;
в) 
;
г) 
.
51. Указать формулу, соответствующую закону элиминации:
а) 
;
б) 
;
в) 
;
г) 
.
52.Указать несобственные подмножествами множества 
:
а) 
;
б) 
;
в) 
;
г)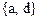 
;
д) 
.
53. Множества имеют одинаковую мощность, если они содержат:
а) одни и те же элементы;
б) одинаковое количество элементов.
54. Кардинальное число определяет:
а) количество элементов булеана данного множества;
б) количество элементов данного множества.
55. Булеан множества 
определяется как:
а)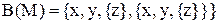 
;
б) 
;
в) 
;
г) 
.
56. Какой закон определяется формулой 
?
а) элиминации;
б) Порецкого;
в) Де Моргана;
г) инволюции
57. Чему равно выражение 
:
а) 
;
б) 
;
в) 
;
г) 
;
д)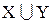 
;
е) 
.
58. Чему равна мощность булеана множества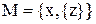 
:
а) 
;
б) 
;
в) 
;
г) 
.
59. Операция объединения двух множеств есть совокупность элементов:
а) различных для этих множеств;
б) принадлежащих одному или другому множеству;
в) принадлежащих обоим множествам.
60. Операция пересечения двух множеств есть совокупность:
а) элементов, одинаковых для этих множеств;
б) элементов, различных для этих множеств;
в) элементов, принадлежащих одному или другому множеству.
61. Операция симметрической разности обозначается символом:
а) 
;
б) 
;
в) 
;
г) 
.
62. Размерность вектора есть:
а) количество всех его компонентов;
б) количество различных его компонентов.
63. Какое из данных соответствий является всюду определенным:
а) б) в)
64. Какое из данных соответствий является функциональным:
а) б) в)
65. Какое из данных соответствий является инъективным:
а) б) в)
66. Какое из данных соответствий является биективным:
а) б) в) г)
67. Какие соответствия не являются инъективными:
а) б)в) г)
68. Какие соответствия не являются функциональными:
а) б) в) г)
69. Какие соответствия являются сюръективными:
а) б) в) г)
70. Какие соответствия являются всюду определенными:
а) б) в) г)
71. Какой из законов не обязательно присутствует в определении решетки:
а) коммутативный;
б) дистрибутивный;
в) элиминации;
г) ассоциативный?
72. Какой закон в дополнение к обязательным определяет решетку как булеву алгебру:
а) дистрибутивный;
б) коммутативный;
в) элиминации;
г) ассоциативный?
73. Решетка определяется на:
а) произвольном множестве;
б) линейно упорядоченном множестве;
в) частично упорядоченном множестве;
г) неупорядоченном множестве?
74. Какое из условий определяет дедекиндову решетку:
а) 
;
б) 
;
в)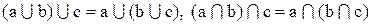 
;
г) 
,
д) 
, 
е) 
75. Какое из условий определяет дистрибутивную решетку в дополнение к свойству модулярности:
а) ;
б) ;
в) 
;
г) ,
д) ,
е)
Комбинаторный анализ
1. Число перестановок из 5 элементов равно:
а) 5; б) 25; в) 120; г) 1.
2. Имеет ли подстановка 
неподвижную точку
а) да;
б) нет.
3. Имеет ли подстановка 
инверсии
а) да;
б) нет.
4. Являются ли перестановки с повторениями различными: А Б С, А Б А?
а) да;
б) нет.
5. Являются ли перестановки различными:
А А Б, А Б А; А В С, А В А;
а) да;
б) нет.
6. Сколькими способами можно расставить на полке 4 книги?
а) 4
б) 4!
в) 
г)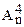 
.
7. Являются ли перестановки с повторениями различными: А А Б, А Б А?
а) да;
б) нет.
8. Выбрать верный вариант:
а) 
при k<n
б) при k>n
9. Биномиальные коэффициенты определяются формулой:
а) 
б) 
в) 
г) 
10. Полиномиальные коэффициенты определяются формулой:
а) 
б)
в) 
г)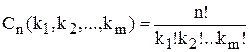 
11. Выбрать верный вариант:
а)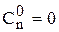 
б) 
в) 
12. Выбрать верный вариант:
а) 
б) 
в) 
13. Выбрать верный вариант:
а) 
б) 
в) 
14. Свойство симметрии биномиальных коэффициентов определяется как:
а) 
б)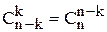 
в) 
15. Сколько существует способов выбрать 3 книги из 5?
а) 0;
б) 1;
в)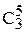 
;
г) 
.
16. Являются ли сочетания с повторениями различными: МАМА, МАША?
а) да;
б) нет.
17. Являются ли сочетания с повторениями различными: ПАПА, АППА?
а) да;
б) нет.
18. Какие из сочетаний с повторениями являются различными?
а) МАМА, МАША;
б) ПАПА, АППА;
в) ПАРА, РАПА.
19. Какие из размещений являются идентичными:
а) abcba, abcba;
б) abc, cba;
в) abce, abc.
20. Какие из сочетаний являются идентичными:
а) 123, 232;
б) abc, cba;
в) КСМ, МСК.
21. Сколькими способами можно рассадить 4 человека на n местах?
а) 4
б) 4!
в) 
г) 
д) 
22. Указать формулу для определения числа размещений:
а) 
б)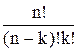 
в) 
23. Какие комбинаторные конфигурации являются упорядоченными:
а) перестановки;
б) размещения;
в) сочетания.
24. В каком случае мощность множества больше:
а) в размещении без повторений;
б) в размещении с повторениями;
в) одинаково.
25. Является ли размещение перестановкой:
а) никогда;
б) всегда;
в) да, при k<n;
г) да, при k=n.
Булева алгебра
1. Сколько двоичных наборов содержит таблица истинности функции f(a,b,c)?
а) 2;
б) 3;
в) 7;
г) 8?
2. Какая из формул допускает упрощение:
а) 
;
б) 
;
в) 
;
г) 
?
3. Какая из формул представляет закон элиминации:
а) 
;
б) 
;
в) 
;
г)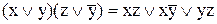 
?
4. Чему равно логическое выражение 
:
а) 0;
б) 
;
в) 
;
г) 1?
5. Предельное дизъюнктивное разложение функции по теореме Шеннона есть
а) СКНФ;
б) СДНФ;
в) ДНФ;
г) КНФ?
6. На каком входном наборе конъюнкция двух переменных равна единице:
а) 0,0;
б) 0,1;
в) 1,0;
г) 1,1.
7. На каком входном наборе дизъюнкция двух переменных равна единице:
а) 0,0;
б) 0,1;
в) 1,0;
г) 1,1.
8. Конъюнкция некоторого числа переменных равна единице, когда:
а) все переменные равны единице;
б) все переменные равны нулю;
в) хотя бы одна переменная равна единице;
г) хотя бы одна переменная равна нулю.
9. Дизъюнкция некоторого числа переменных равна единице, когда:
а) все переменные равны единице;
б) все переменные равны нулю;
в) хотя бы одна переменная равна единице;
г) хотя бы одна переменная равна нулю.
10. Чему равно выражение 
:
а) 
;
б) 
;
в) 
;
г)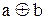 
?
11. Какой элемент реализует функцию логического сложения:
а)
б)
в)
г)
12. Какой элемент реализует функцию логического умножения:
а)
б)
в)
г)
13. Какой функциональный элемент соответствует сумме по модулю 2:
а)
б)
в)
г)
14. Какой элемент соответствует функции равнозначности:
а)
б)
в)
г)
15. Функция 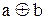является самодвойственной?
а) да;
б) нет.
16. Функция 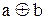является:
а) сохраняющей единицу;
б) сохраняющей ноль;
в) монотонной?
17. Функция 
является:
а) самодвойственной;
б) сохраняющей единицу;
в) сохраняющей ноль;
г) монотонной?
18. Какие из кубов представляют точку:
а) 0-куб;
б) 1-куб;
в) 2-куб;
г) любой.
19. Какие из кубов задают отрезок:
а) 0-куб;
б) 1-куб;
в) 2-куб;
г) любой.
20. Какие из кубов представляют плоскость:
а) 0-куб;
б) 1-куб;
в) 2-куб;
г) любой.
21. Указать куб, который геометрически можно интерпретировать как плоскость:
а) Х00;
б) 0ХХ;
в) 101;
г) любой.
22. Указать куб, который геометрически можно интерпретировать как отрезок:
а) Х0Х;
б) 01Х;
в) 101;
г) любой.
23. Указать куб, который геометрически можно интерпретировать как точку:
а) 100;
б) 0ХХ;
в) 10Х;
г) любой.
24. Куб 1Х1 геометрически можно интерпретировать как:
а) плоскость;
б) отрезок;
в) точку.
25. Указать, какие кубы склеиваются:
а) Х00, Х10;
б) 011, 100;
в) 10Х, 01Х;
г) ни одна пара не склеивается.
26. Склеивание кубов 010 и 011 дает:
а) Х00;
б) 0ХХ;
в) 101;
г) 01Х.
27. Куб ХХ1 является
а) 1-кубом;
б) 2-кубом;
в) 0-кубом.
28. Куб 00Х является
а) 1-кубом;
б) 2-кубом;
в) 0-кубом.
29. Куб 011 является
а) 1-кубом;
б) 2-кубом;
в) 0-кубом.
30. Каждая импликанта в СДНФ соответствует
а) нулевому значению функции;
б) значению функции, равному единице.
31. Каждая импликанта в СКНФ соответствует
а) нулевому значению функции;
б) значению функции, равному единице.
32. Первая производная функции по переменной x равна 
. Какие значения сигналов не являются условием возможной активизации выхода при изменении сигнала x:
а) 1,0;
б) 0,1;
в) 1,1;
г) 0,0?
33. Альтернативное понятие для минимизации есть:
a) факторизация;
б) поглощение;
в) булевизация;
Г) разложение.
34. Поставить в соответствие функциям их таблицы истинности:
1) а b c d
2) а b c d
3) а b c d
4) а b c d
35. Поставить в соответствие кубическим покрытиям их таблицы истинности:
1) а b c d
2) а b c d
3) а b c d
4) а b c d
36. Разложение булевой функции по Шеннону предназначено для:
а) факторизации;
b) максимизации;
c) минимизации;