Объемы потребления 20 50 20 35
Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Решение
На рис.3.1 представлено введенное условие и решение транспортной задачи.
Ячейку С17 введена формула =СУММПРОИЗВ(C10:F13;C2:F5)
В ячейку С 14 введена формула =СУММ(C10:C13), формулу протянут до ячейки F14
В ячейку G10 введена формула =СУММ(C10:F10), протянем формулу до ячейки G13.
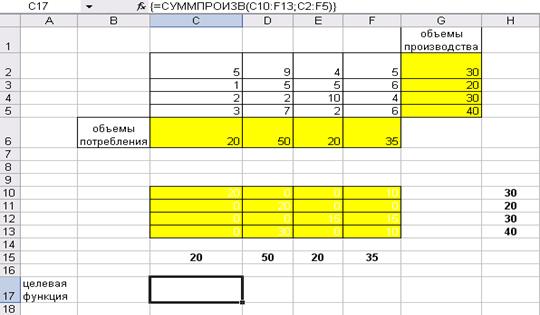
Рис.3.1 – Ввод данных задачи 3.1 в Excel
На рис.3.2 представлено решение задачи через меню Сервис – Поиск решения.
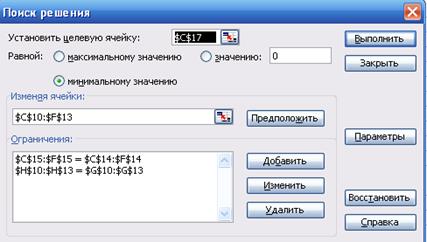
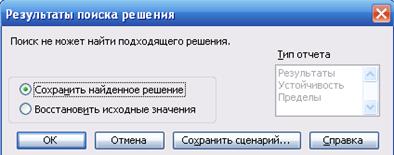
Рисунок 3.2 - Поиск решения
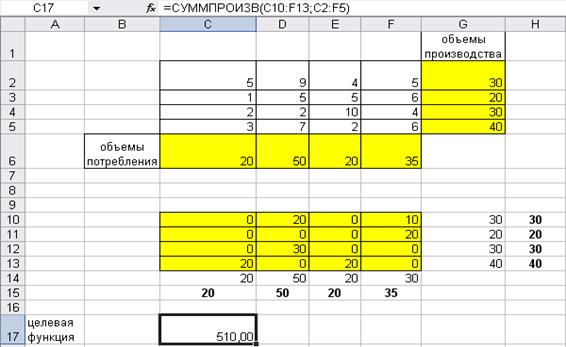
Поиск решения не может найти подходящего решения, так как объемы производства не равны объемам потребления. Разница составляет 2 единицы (сумма объемов 120 и 125). Задача открытая, её необходимо закрыты путем введения фиктивного пункта производства. Для этого добавим строку с объемом производства равным 5. И решение повторим.

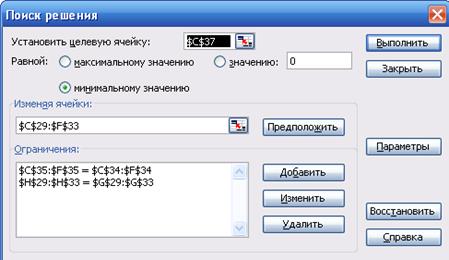
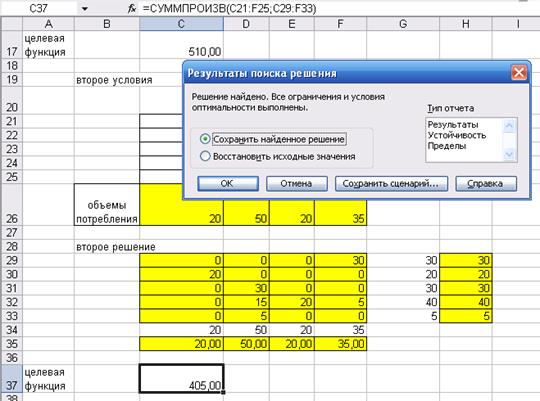
Рисунок 3. 4– Повторное решение задачи 3.1.
Ответ: суммарные минимальные затраты составят 405 ден. единиц. При этом план перевозок будет следующим:
Задача 3.2.
Задача о назначениях. Имеются n рабочих и m видов работ. Стоимость с[i,j] выполнения i-м рабочим j-й работы приведена в таблице, где рабочему соответствует строка, а работе – столбец.
Стоимость выполнения работ
| |||||
Виды работ
Необходимо составить план работ так, чтобы все работы были выполнены, каждый рабочий был занят только на одной работе, а суммарная стоимость выполнения всех работ была бы минимальной.
Решение
На рис.3.5. представлено пошаговое решение задачи
Шаг1

Шаг 2
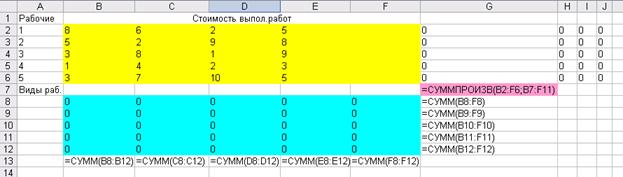
Шаг 3
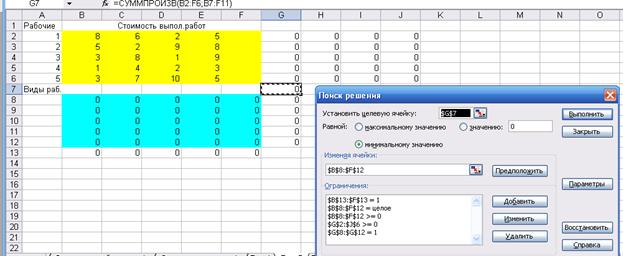
Шаг4
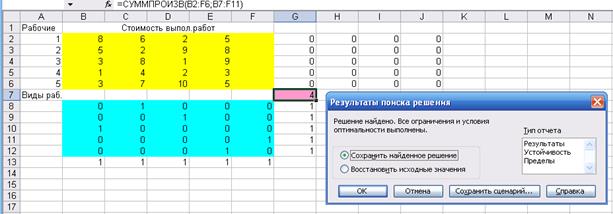
Рисунок 3. 5 – Решение задачи 3.2
Ответ: суммарная стоимость выполнения всех работ составит 4 ден. единиц, при этом план работ следующий:
Задача 3.3.
Линейная оптимизационная задача.
Завод выпускает изделия трех моделей(1, 2, 3). Для их изготовления используются два вида ресурсов(А и В), запасы которых составляют 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели приведены в таблице 3.7.
Таблица 3.7. Расходы ресурсов
| Ресурс | Расход ресурса на одно изделие данной модели | ||
| А В |
Трудоемкость изготовления изделия модели 1 вдвое больше, чем изделия модели 2, и втрое больше, чем изделия модели 3. Численность рабочих завода позволяет выпускать 1500 изделий модели 1. Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей 1, 2, 3, соответственно. Однако соотношение выпуска изделий моделей 1, 2, 3 должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей 1, 2, 3 составляет 30, 20 и 50 долларов соответственно. Определить выпуск изделий, максимизирующий прибыль.
Решение
На рис. 3.6. представлено по шаговое (5 шагов) решение задачи.
Шаг 1
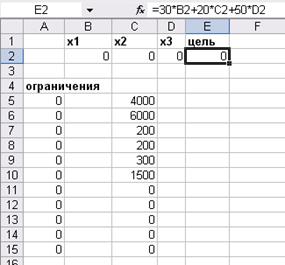
Шаг 2
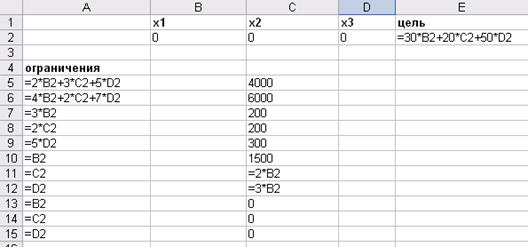
Шаг 3
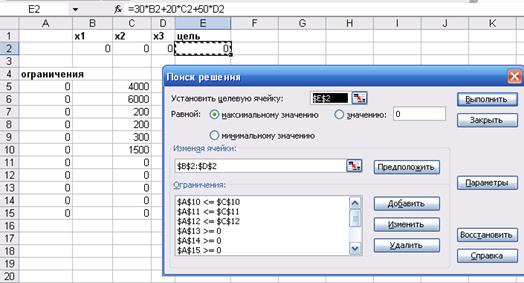
Шаг 4
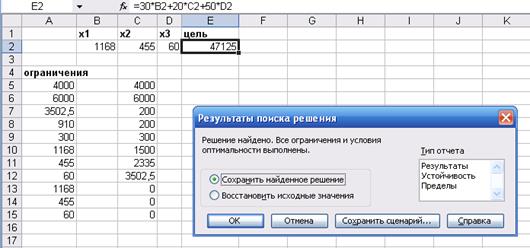
Рисунок 3.6. – Пошаговое решение задачи 3.3
Ответ: для получения максимальной прибыли в размере 47125 грн., необходимо произвести 1168 ед. 1 изделия, 455 ед. – 2 изделия и 60 ед. – 3 изделия.
Задача 3.4.
Система нелинейных уравнений.

Найти все решения системы нелинейных уравнений.
Решение
На рис.3.7 представлено по шаговое (5 шагов) решение задачи.
Шаг1

Шаг 2
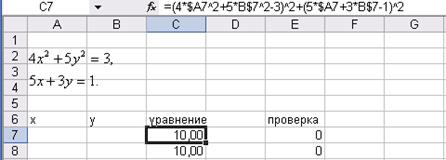
Шаг 3

Шаг 4
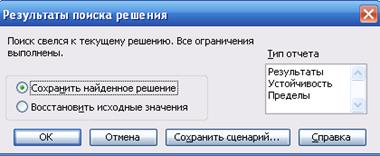
Шаг 5
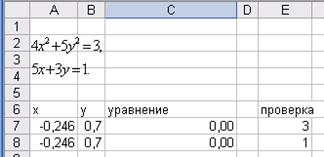
Рисунок 3.7 – Пошаговое решение задачи 3.4
Ответ: х = -0,246 у = 0,7
Задача 3.5.
Уравнение регрессии. Построить линейную модель для двух наблюдаемых величин (например, объем реализованных фирмой подержанных автомобилей за указанное число недель).
| Неделя | ||||||||
| Количество машин |
Решение
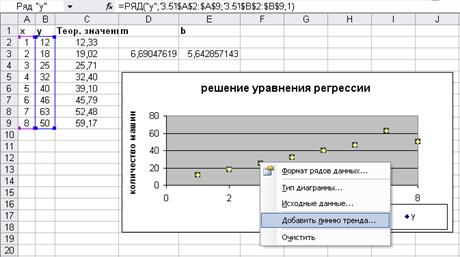
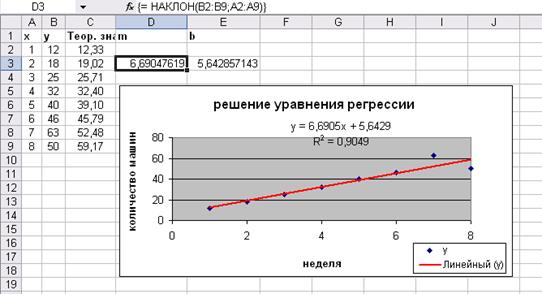
В ячейку D3 введем формулу = НАКЛОН(B2:B9;A2:A9)
В ячейку Е3 введем формулу =ОТРЕЗОК(B2:B9;A2:A9)

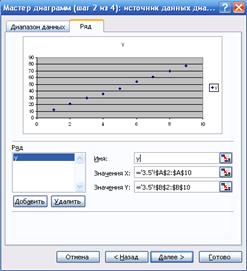
Строим график.
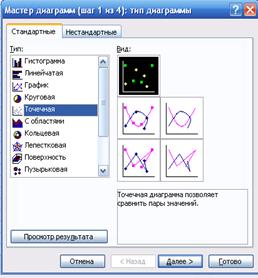
| 
| ||
| 
| ||
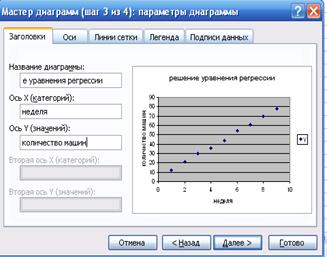
Результат построения графика.

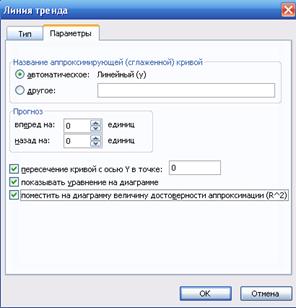
Добавляем линию тренда