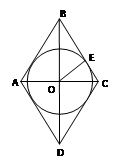
Задача 7: в ромб вписана окружность радиуса R. Найти площадь ромба, если его большая диагональ в 4 раза больше радиуса вписанной окружности.
Дано: ромб, радиус вписанной окружности – R, BD 
r в 4 раза
Найти: 
 |
Решение:
1. Пусть OE = R, BD = 4OE = 4R
2. 
3. 
4. 
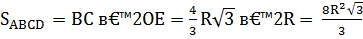
Ответ: 
Задача 8: найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Дано: ABCD – равнобедренная трапеция, r = 4, AB = 10
Найти: 
 |
Решение:
1. AB = CD = 10 по условию
2. AB + CD = AD + BC по свойству вписанной окружности
3. AD + BC = 10 + 10 = 20
4. FE = 2r = 2 · 4 = 8
5. 
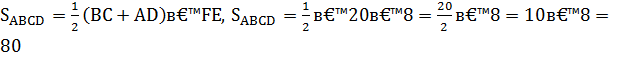
Ответ: 
Задача 9: внутри правильного треугольника со стороной a расположены три равные окружности, каждая из которых касается двух сторон треугольника и двух других окружностей. Найти площадь части треугольника, расположенной вне этих окружностей.
 |
Решение:
1. Пусть AB = BC = AC = a.
2. Обозначим O1E = O1K = ED = r, тогда AD = AE + ED = AE + r = 
.
3. AO1 – биссектриса угла A, следовательно, ﮮ O1AE = 30˚ и в прямоугольном ∆AO1E имеем AO1 = 2O1E = 2r и AE = 
= 
= 
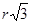. Тогда AE + r = = 
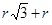= , откуда 
.
4. 
Ответ: 
Задача 10: вся дуга окружности радиуса R разделена на 4 большие и 4 малые части, которые чередуются одна за другой. Большая часть в два раза длиннее малой. Определить площадь восьмиугольника, вершинами которого являются точки деления дуги окружности.
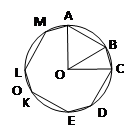
Решение:
1. Пусть ﮮAOB = 2x, ﮮBOC = x, тогда по условию 8x + 4x = 360°, x = 30°, 2x = 60°, ﮮAOB = 60°, ﮮBOC = 30°
2. 
3. 
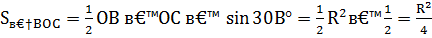
4. 
Ответ: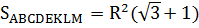 
Задача 11: стороны треугольника равны 12 м, 16 м и 20 м. Найдите го высоту, проведенную из вершины большего угла.
 |
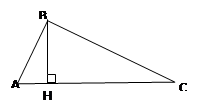Решение:
1. 202 = 122 + 162
400 = 144 + 256
400 = 400 верно, следовательно, ∆ АВС – прямоугольный (по теореме, обратной теореме Пифагора)
|
|
2. 
3. 
96 = 10 · ВН
ВН = 9,6
Ответ: ВН = 9,6
Задача 12: в прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найдите площадь квадрата, если катеты треугольника равны 10 м и 15 м.
Дано: ∆ ABC – прямоугольный, AC = 15, CB = 10
Найти: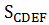 
Решение:
1. ∆ ADE ~ ∆ ACB (ﮮ A – общий, ﮮ ADE = ﮮ ACB = 90°)
2. Пусть DE = DC = X, тогда AD = 15 – X
3. 
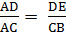
15 · X = 10(15 – X)
15 · X = 150 – 10 · X
25 · X = 150
X = 6
DE = DC = 6
4. S кв. = 6 · 6 = 36
Ответ: S кв. = 36
Задача 13: основания трапеции равны 10 м и 31 м, а боковые стороны – 20 м и 13 м. Найдите высоту трапеции.
 |
Решение:
1. HK = BC = 10 м
2. Пусть BH = CK = x, AH=y, тогда KD = 21 – y
3. По теореме Пифагора:
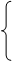x2 + y2 = 132
x2 + (21 – y)2 = 202
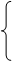x2 + y2 = 169
x2 + 441 – 42y + y2 = 400
441 – 42y = 231
42y = 210
y = 5
AH = 5 м
4. По теореме Пифагора:
BH2 = AB2 – AH2
BH2 = 132 – 52
BH2 = 169 – 25
BH2 = 144
BH = 12
Ответ: BH = 12
Заключение
В процессе работы я расширил знания по теме «Вписанные и описанные окружности в треугольниках и четырехугольниках», научился решать задачи, казавшиеся ранее недоступными, систематизировал знания по этой теме, и закрепил методы решения этих задач на практике.
Так как геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы, то в дальнейшем мне будет намного легче справиться с ними на ЕГЭ.
Список литературы:
1. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
2. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
|
|
3. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
4. Т. А. Корешкова, Ю. А. Глазков, В. В. Мирошин, Н. В. Шевелева «Математика. Единый государственный экзамен 2006. Типовые тестовые задания»