Задача Д1
Условие. Груз D массой m, получив в точке А начальную скорость  , движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила
, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила 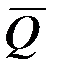 (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды 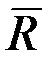 , зависящая от скорости
, зависящая от скорости  груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу
груза (направлена против движения); трением груза о трубу на участке АВ пренебречь. В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу  =0,2),а переменная сила
=0,2),а переменная сила 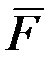 , проекция которой
, проекция которой  на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ=
на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ=  или время
или время 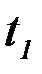 движения груза от точки А до точки В,найти закон движения груза на участке ВС,т. е.
движения груза от точки А до точки В,найти закон движения груза на участке ВС,т. е. 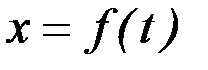 , где х=BD.
, где х=BD.
Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t =0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти к переменному x, учтя, что
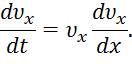

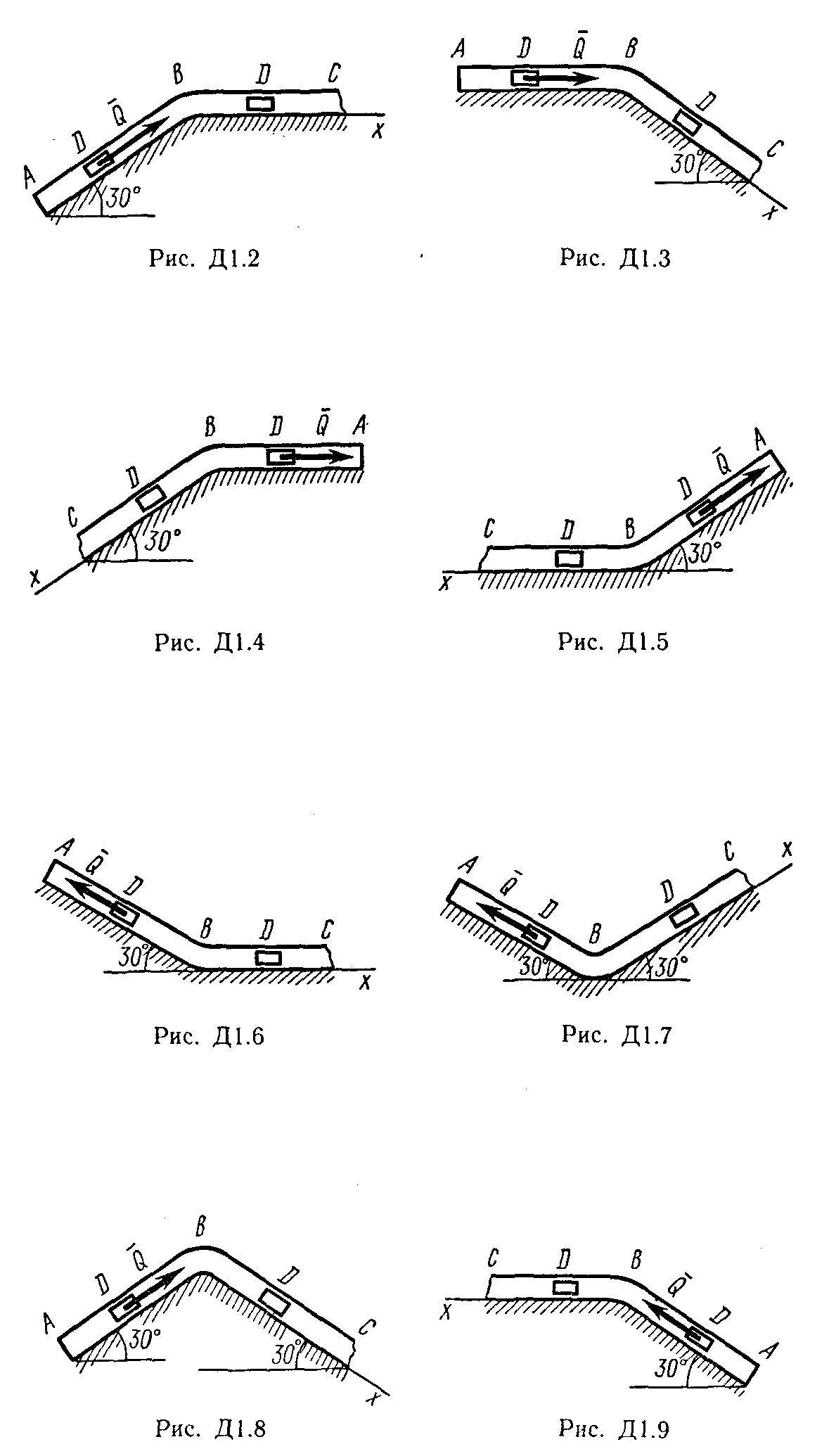
Таблица Д1
| №условия | m, кг | 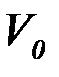 , м/с , м/с
| Q, Н | R, Н | l, м |  , с , с
|  , Н , Н
|
| 0,4V | – | 2,5 | 2sin(4t) | ||||
| 2,4 | 0,8V2 | 1,5 | – | 6t | |||
| 4,5 | 0,5V | – | 3sin(2t) | ||||
| 0,6V2 | – | -3cos(2t) | |||||
| 1,6 | 0,4V | – | 4cos(4t) | ||||
| 0,5V2 | – | -6sin(2t) | |||||
| 1,8 | 0,3V | – | 9t2 | ||||
| 0,8V2 | 2,5 | – | -8cos(4t) | ||||
| 0,5V | – | 2cos(2t) | |||||
| 4,8 | 0,2V2 | – | -6sin(4t) |
Пример выполнения задачи Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой m действуют сила тяжести и сила сопротивления R; расстояние от точки А, где υ=υ0, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F=F(t), заданная в ньютонах.
Дано: m=2 кг, R= 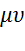 2 , где
2 , где  кг/м, υ0=5 м/с, l=2,5 м, Fx=16sin(4t). Определить: x=f(t) – закон движения груза на участке ВС.
кг/м, υ0=5 м/с, l=2,5 м, Fx=16sin(4t). Определить: x=f(t) – закон движения груза на участке ВС.
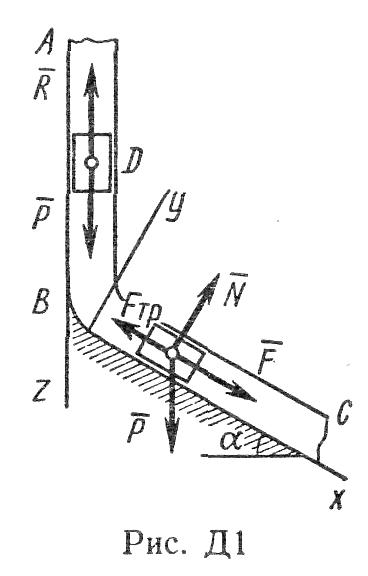
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы 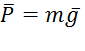 и
и 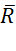 . Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
. Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:
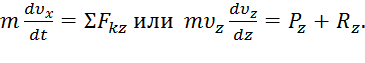 (1)
(1)
Далее находим 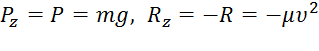 ; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υ z=υ, получим
; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υ z=υ, получим
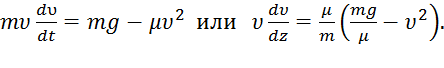 (2)
(2)
Введем для сокращения записей обозначения
 (3)
(3)
где при подсчете принято g≈ 10м/с2. Тогда уравнение (2) можно представить в виде
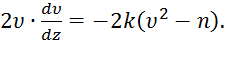 (4)
(4)
Разделяя в уравнении (4) переменные, а затем, беря от обеих частей интегралы, получим
 (5)
(5)
По начальным условиям при  , что дает
, что дает 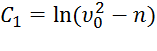 и из равенства (5) находим
и из равенства (5) находим 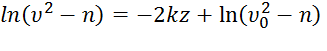
или 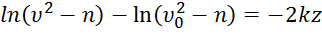 . Отсюда
. Отсюда
 .
.
В результате находим
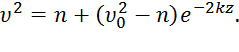 (6)
(6)
Полагая в равенстве (6) z=l= 2,5 м и заменяя k и n их значениями (3), определим скорость 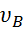 груза в точке В (
груза в точке В (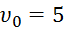 м/с, число e= 2,7):
м/с, число e= 2,7):
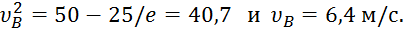 (7)
(7)
2. Рассмотрим теперь движение груза на участке ВС; найденная скорость  будет для движения на этом участке начальной скоростью (
будет для движения на этом участке начальной скоростью ( ). Изображаем груз (в произвольном положении) и действующие на него силы
). Изображаем груз (в произвольном положении) и действующие на него силы 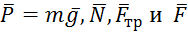 и. Проведем из точки В оси Вх и Ву и составим дифференциальное уравнение движения груза в проекции на ось Вх:
и. Проведем из точки В оси Вх и Ву и составим дифференциальное уравнение движения груза в проекции на ось Вх:
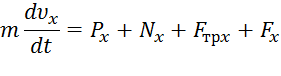
или
 , (8)
, (8)
где  . Для определения N составим уравнение в проекции на ось Ву. Так как ay=0, получим 0=N – mgcosα, откуда N=mgcosα. Следовательно,
. Для определения N составим уравнение в проекции на ось Ву. Так как ay=0, получим 0=N – mgcosα, откуда N=mgcosα. Следовательно, 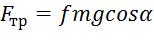 ; кроме того,
; кроме того, 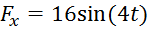 и уравнение (8) примет вид
и уравнение (8) примет вид
m 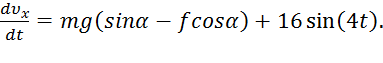 (9)
(9)
Разделив обе части равенства на m, вычислим  и подставим эти значения в (9). Тогда получим
и подставим эти значения в (9). Тогда получим
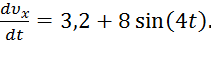 (10)
(10)
Умножая обе части уравнения (10) на dt и интегрируя, найдем
 (11)
(11)
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 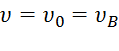 , где
, где  дается равенством (7). Подставляя эти величины в (11), получим
дается равенством (7). Подставляя эти величины в (11), получим
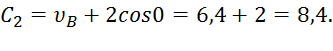
При найденном значении 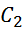 уравнение (11) дает
уравнение (11) дает
 (12)
(12)
Умножая здесь обе части на dt и снова интегрируя, найдем
 (13)
(13)
Так как при t=0 x=0, то  и окончательно искомый закон движения груза будет
и окончательно искомый закон движения груза будет
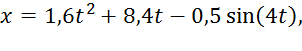 (14)
(14)
где x – в метрах, t – в секундах.
Контрольные вопросы:
1. Что такое динамика?
2. Сформулировать законы динамики
3. Задачи динамики
4. Сформулировать вторую (основную) задачу динамики
5. Как определяются постоянные интегрирования?
6. Как определить уравнения движения точки при криволинейном движении?
7. В каких единицах измерения определяется сила?
8. Записать в общем виде дифференциальное уравнение прямолинейного движения точки
9. Записать в общем виде дифференциальное уравнение прямолинейного движения в пространстве
10. Что такое начальные условия?
Задача Д 2.
Условие. Груз l массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 – Д2.9, табл. Д2). Лифт движется вертикально по закону 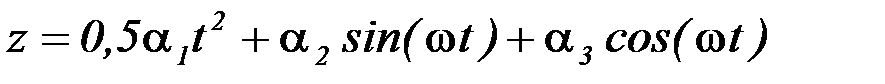 (ось z направлена по вертикали вверх; z выражено в метрах, t – в секундах). На груз действует сила сопротивления среды
(ось z направлена по вертикали вверх; z выражено в метрах, t – в секундах). На груз действует сила сопротивления среды 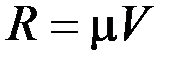 , где
, где 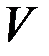 – скорость груза по отношению к лифту.
– скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. 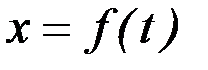 ; начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором
; начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором 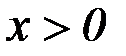 , т.е. пружина растянута. При подсчетах можно принять
, т.е. пружина растянута. При подсчетах можно принять 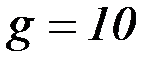 м/с2. Массой пружины и соединительной планки 2 пренебречь.
м/с2. Массой пружины и соединительной планки 2 пренебречь.
В таблице обозначено: 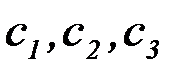 – коэффициенты жесткости пружин,
– коэффициенты жесткости пружин, 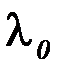 – удлинение пружины с эквивалентной жесткостью в начальный момент времени
– удлинение пружины с эквивалентной жесткостью в начальный момент времени 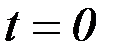 ,
, 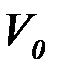 – начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах
– начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах 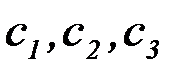 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие 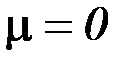 означает, что сила сопротивления
означает, что сила сопротивления 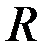 отсутствует.
отсутствует.
Указания. Задача Д2 охватывает одновременно относительное движение и колебания материальной точки.
Сначала нужно составить дифференциальное уравнение относительного движения (по отношению к лифту) рассматриваемого в задаче груза, для чего присоединить к действующим силам переносную силу инерции. Затем прикрепленные к грузу пружины (по условию задачи их будет две) заменить эквивалентной пружиной с коэффициентом жесткости сэкв=с, произведя соответствующий расчет.
а) Если пружины соединены друг с другом последовательно (как пружины с жесткостями с1 и с2 на рис. Д2.0), то при равновесии под действием некоторой силы 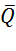 , приложенной к свободному конце пружины, усилия в любом поперечном сечении пружин одинаковы и равны Q. Удлинения пружин
, приложенной к свободному конце пружины, усилия в любом поперечном сечении пружин одинаковы и равны Q. Удлинения пружин  , удлинение эквивалентной пружины
, удлинение эквивалентной пружины 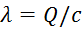 и
и 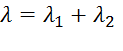 . Отсюда
. Отсюда

б) Если груз прикреплен к двум параллельным пружинам (как к пружинам с жесткостями с1 и с2 на рис. Д2.1) или находится между двумя пружинами, то при равновесии под действием некоторой силы 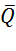 каждая из пружин и эквивалентная пружина имели бы одно и то же удлинение λ. Тогда для двух пружин
каждая из пружин и эквивалентная пружина имели бы одно и то же удлинение λ. Тогда для двух пружин 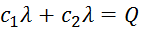 , а для эквивалентной пружины сλ=Q, отсюда c=
, а для эквивалентной пружины сλ=Q, отсюда c= 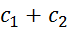 .
.
После того как уравнение будет составлено (это будет линейное дифференциальное уравнение 2-го порядка), его следует проинтегрировать, учтя начальные условия.
Таблица Д2
| Номер условия | m, кг | С1 Н/м | С2 Н/м | С3 Н/м | α1, м/с2 | α2, м/с2 | α3, м/с2 | ω, 1/с | µ, Н· с/м | λ0, м | V0, м/с |
| – | 0,1 | ||||||||||
| 0,8 | – | -1,5g | – | 0,1 | |||||||
| 0,5 | – | 0,8 | |||||||||
| – | 0,5 | ||||||||||
| 0,5 | – | -g | – | 0,15 | |||||||
| – | 0,1 |
Продолжение таблицы Д2
| 0,4 | – | g | – | ||||||||
| 0,5 | – | 0,1 | |||||||||
| 0,4 | – | 0,2 | 0,15 | ||||||||
| – | 1,5g | – |
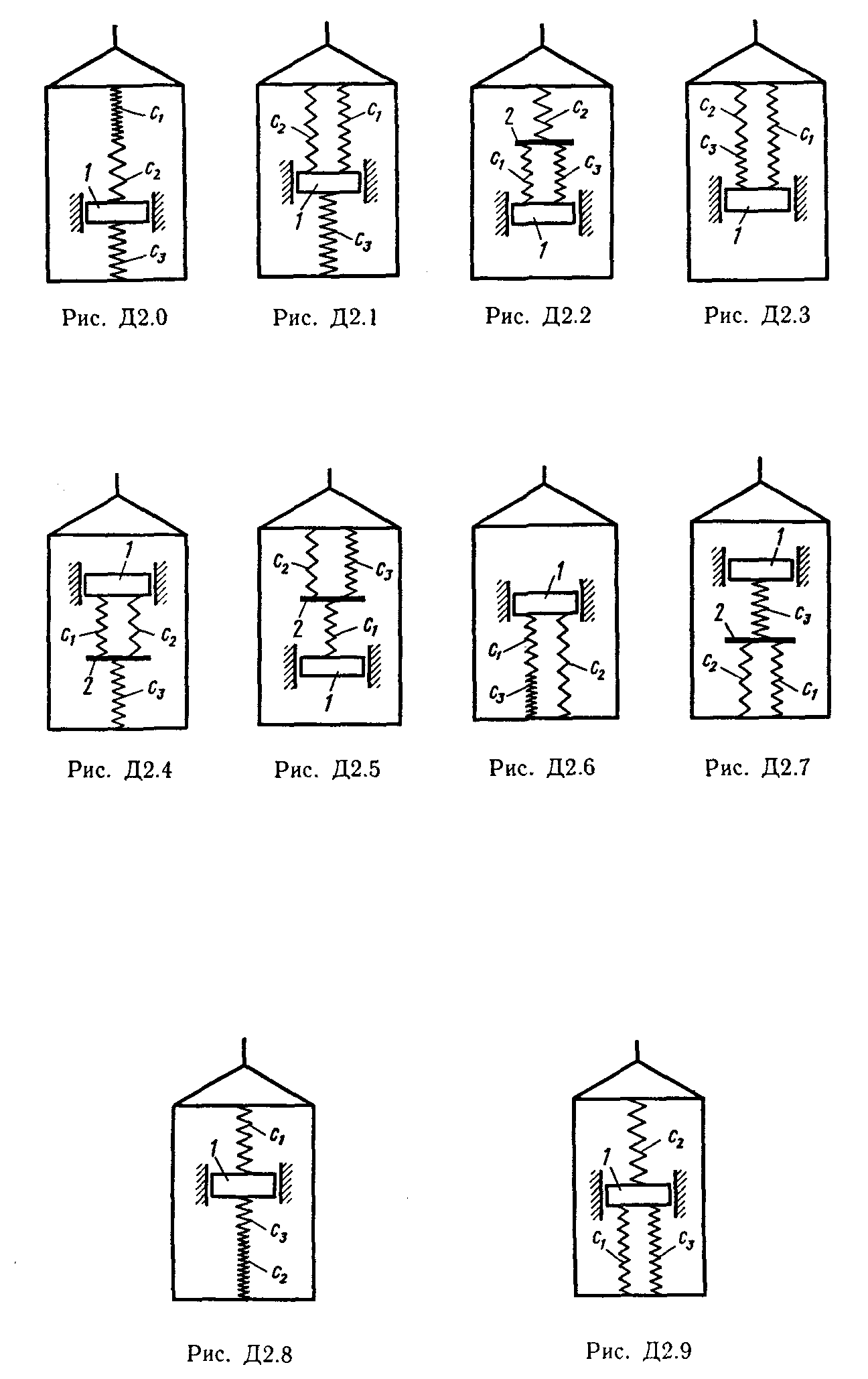
Пример выполнения задачи Д2. В приборе для измерения вертикальных колебаний (рис. Д2) груз массой m прикреплен к пружине с коэффициентом жесткости с. Другой конец пружины прикреплен к корпусу прибора, который движется по закону  (неподвижная ось z направлена по вертикали вниз). начальное удлинение пружины равно λ0 , а начальная скорость груза по отношению к корпусу прибора υ0 (направлена вертикально вниз).
(неподвижная ось z направлена по вертикали вниз). начальное удлинение пружины равно λ0 , а начальная скорость груза по отношению к корпусу прибора υ0 (направлена вертикально вниз).
Дано: m=0,4 кг, c=40 Н/м, λ0=0,05 м, υ0=0,5 м/с, A =0,03 м, ω=20 l/c.
Определить: x=f(t) - закон движения груза по отношению к корпусу прибора.
Решение. 1. Свяжем с корпусом прибора подвижную систему отсчета, начало О которой поместим в конце недеформированной пружины (ее длина обозначена l0), а ось х направим в сторону удлинения пружины (см. рис. Д2).

Рассмотрим груз в положении, при котором пружина растянута. На груз действует сила тяжести 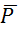 и сила упругости
и сила упругости  . Для составления уравнения относительного движения груза, присоединим к этим силам переносную силу инерции
. Для составления уравнения относительного движения груза, присоединим к этим силам переносную силу инерции 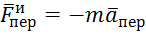 , кориолисова сила инерции равна нулю, так как переносное движение (движение корпуса прибора) является поступательным. Тогда уравнение относительного движения в векторной форме будет иметь вид
, кориолисова сила инерции равна нулю, так как переносное движение (движение корпуса прибора) является поступательным. Тогда уравнение относительного движения в векторной форме будет иметь вид

Проектируя обе его части на ось х, получим
 . (1)
. (1)
Здесь 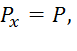
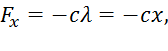 где
где  удлинение пружины,
удлинение пружины,  . Учитывая, что оси х и z направлены одинаково, получим
. Учитывая, что оси х и z направлены одинаково, получим 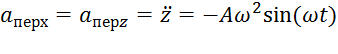 и
и 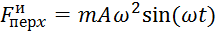 .
.
Подставляя все найденные выражения проекций сил в уравнение (1), получим
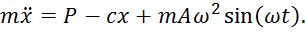 (2)
(2)
Дифференциальное уравнение (2) может быть записано в виде
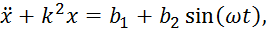 (3)
(3)
где обозначено
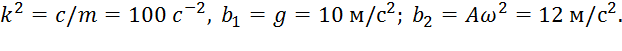 (4)
(4)
2. Для определения закона движения груза надо проинтегрировать уравнение (3). Его общее решение, как известно из теории дифференциальных уравнений:
 , (5)
, (5)
где x1 – общее решение однородного уравнения  , т.е.
, т.е.
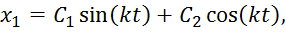 (6)
(6)
а x2 – частное решение уравнения (3). Учитывая, каковы правая и левая части этого уравнения, ищем x2 в виде
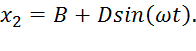 (7)
(7)
Для определения постоянных B и D находим 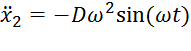 , подставляем значения
, подставляем значения  и
и  в уравнение (3) и приравниваем в его обеих частях свободные члены и коэффициенты при
в уравнение (3) и приравниваем в его обеих частях свободные члены и коэффициенты при 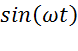 . В результате, принимая во внимание обозначения (4), получим
. В результате, принимая во внимание обозначения (4), получим

Тогда из равенств (5) – (7), учитывая, что 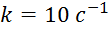 , а
, а  , получим следующее общее решение уравнения (3):
, получим следующее общее решение уравнения (3):
 (10)
(10)
Для определения постоянных интегрирования C1 и C2 найдем еще  ;
;
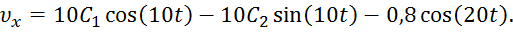 (9)
(9)
По условиям задачи при 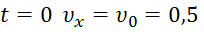 м/с,
м/с, 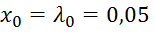 м. Подставив эти начальные данные в уравнения (8) и (9), найдем из них, что
м. Подставив эти начальные данные в уравнения (8) и (9), найдем из них, что 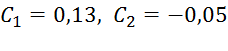 . В результате уравнение (8) примет окончательный вид
. В результате уравнение (8) примет окончательный вид
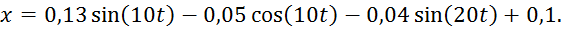 (10)
(10)
Это уравнение и определяет искомый закон относительного движения груза, т.е. закон совершаемых им колебаний.
Контрольные вопросы:
1. Что такое колебательное движение точки?
2. Что такое свободные колебания?
3. Что такое затухающие колебания?
4. Что такое вынужденные колебания?
5. Что такое резонанс?
6. Как определить направление вектора силы инерции при относительном движении точки?
7. Сформулировать правило определения значения эквивалентной жесткости при последовательном соединении двух пружин
8. Сформулировать правило определения значения эквивалентной жесткости при последовательном соединении двух пружин
9. Что такое неинерциальная система отсчета?
10. Как записать уравнение второго закона Ньютона для неинерциальной системы отсчета?
Задача Д5
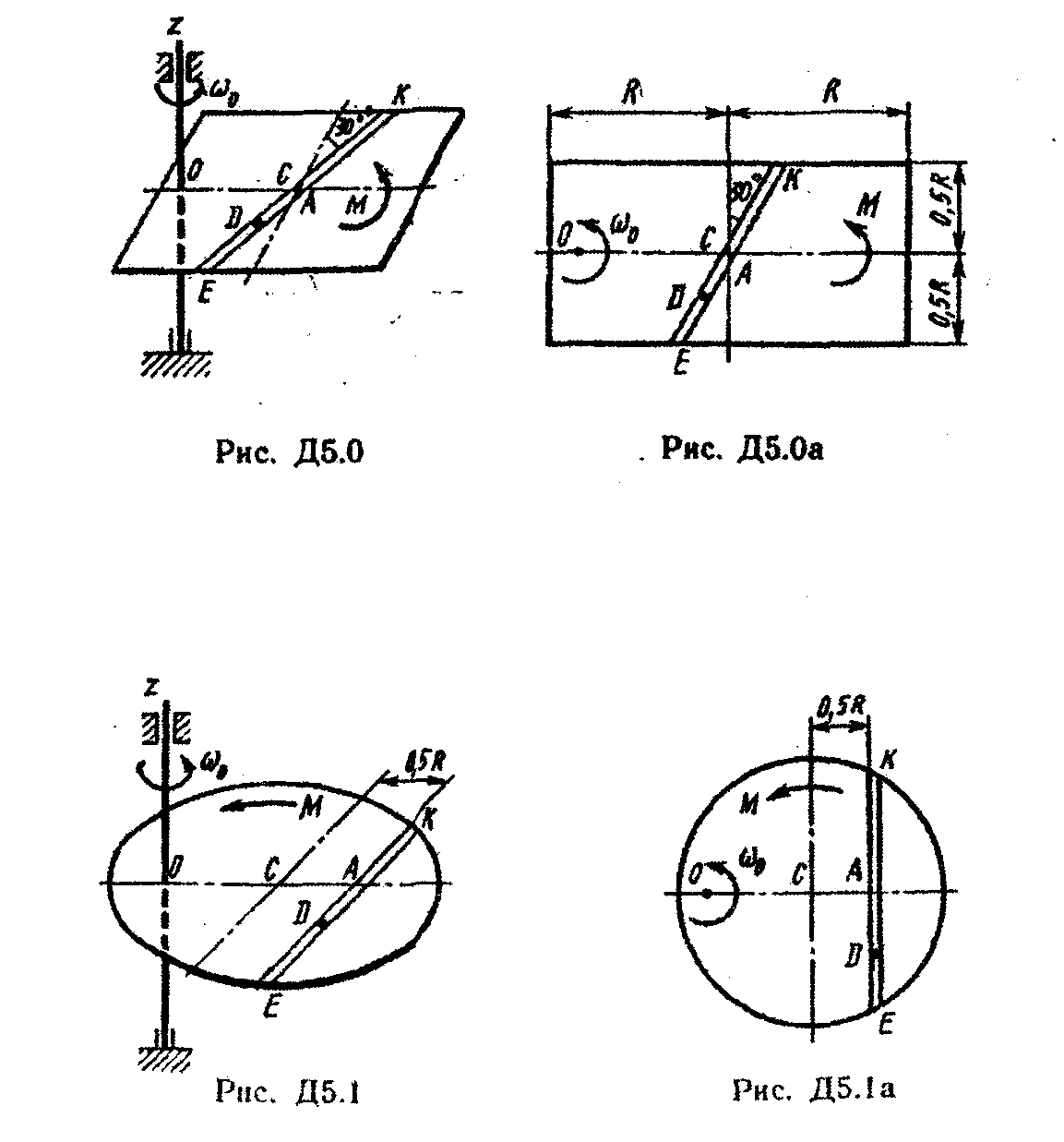
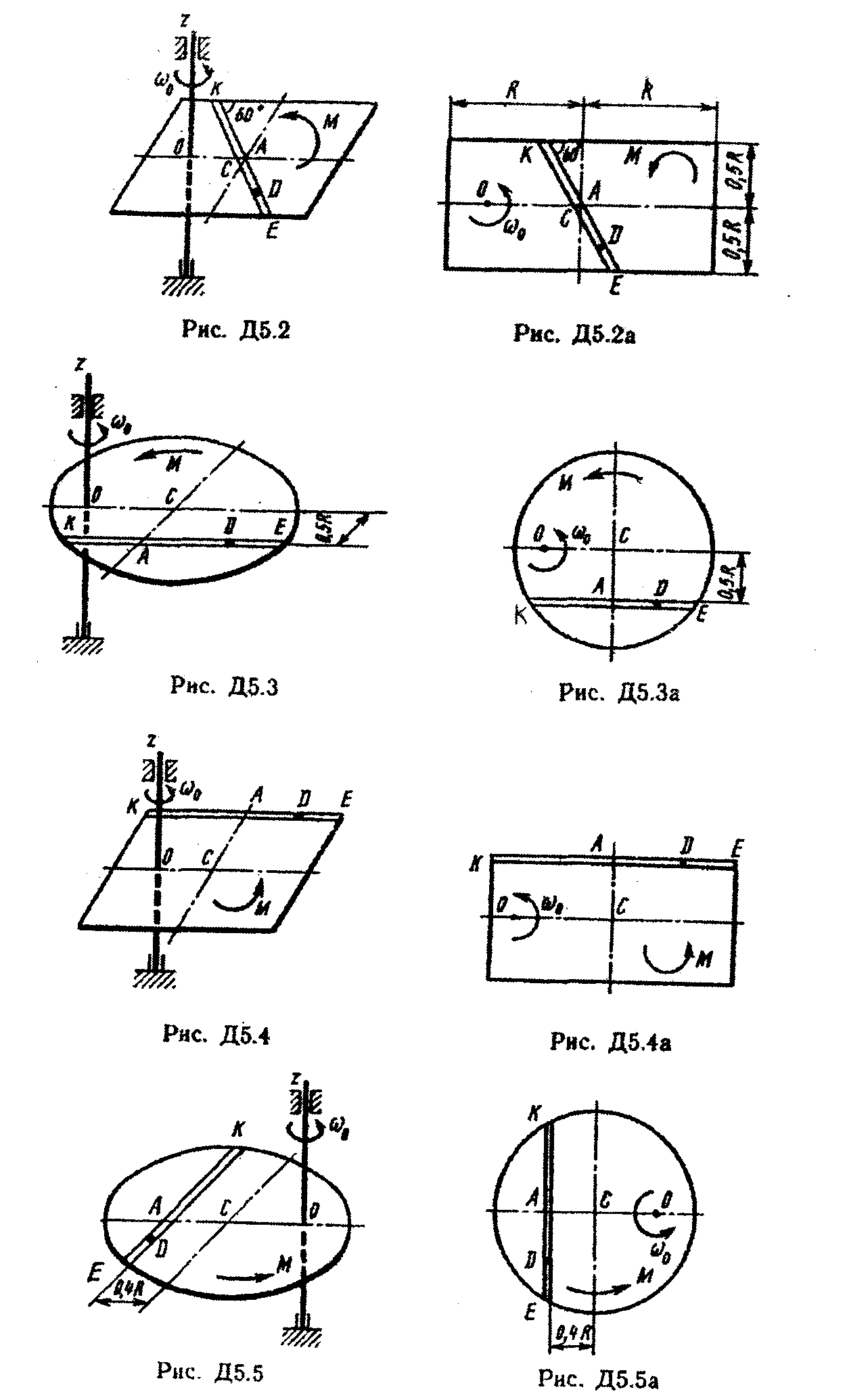
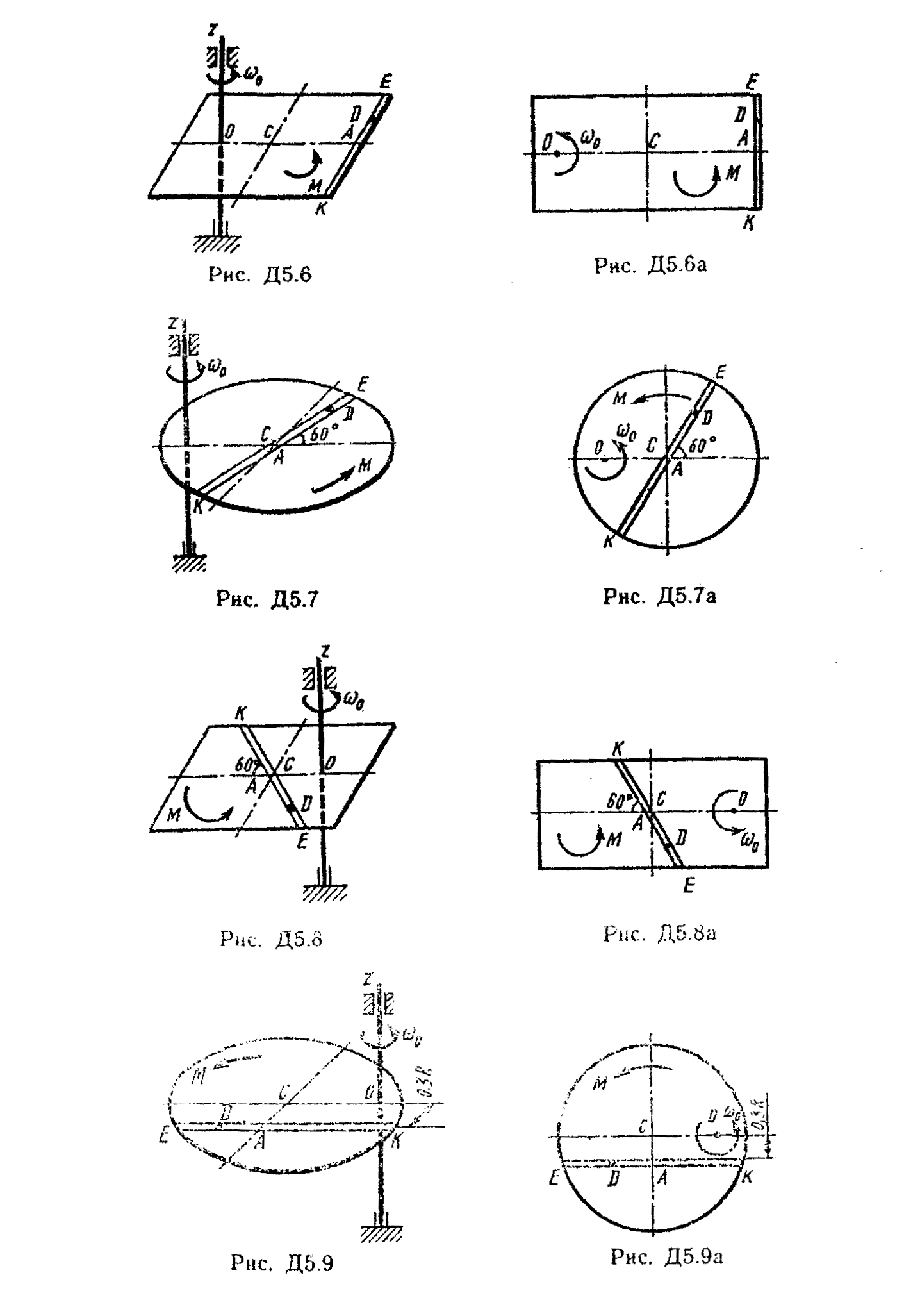
Условие. Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R = 1,2 м.) массой m1 = 24кг вращается с угловой скоростью ω0 = 10 c-1 вокруг вертикальной оси z, отстоящей из центра масс С платформы на расстоянии ОС = b (рис. Д5.0 – Д5.9, табл. Д5); размеры для всех прямоугольных платформ показаны на рис. Д5.0а (вид сверху).
В момент времени t = 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой m2 = 8кг по закону s = AD = F(t), где s выражено в метрах, t – в секундах. Одновременно на платформы начинает действовать пара сил с моментом М (задан в ньютонометрах; при М <0 его направление противоположно показанному на рисунках).
Определить, пренебрегая массой вала, зависимость ω = f(t), т.е. угловую скорость платформы, как функцию времени.
На всех рисунках груз D показан в положении, при котором s>0 (когда s<0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии ОС =b от центра С.
Указания. Задача Д5 – на применение теоремы об изменении кинетического момента системы. При изменении теоремы к системе, состоящей из платформы и груза, кинетический момент Кz системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость груза складывается из относительной 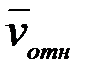 и переносной
и переносной 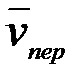 скоростей, т.е.
скоростей, т.е. 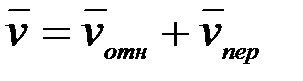 . Поэтому и количество движения этого груза
. Поэтому и количество движения этого груза  . Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой
. Тогда можно воспользоваться теоремой Вариньона (статика), согласно которой  ; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д5.
; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения разъяснен в примере Д5.
При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца оси z), как это сделано на рис. Д5.0 – Д5.9,а.
Момент инерции пластины с массой m относительно оси С z, перпендикулярной пластине и проходящей через ее центр масс С, равен:
для прямоугольной пластины со сторонами а1 и а2
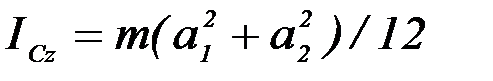 ;
;
для круглой пластины радиуса R

Таблица Д5
| Номер условия | b | s = F(t) | M |
| R R/2 R R/2 R R/2 R R/2 R R/2 | -0.4t2 0.6t2 -0.8t2 10t 0.4t3 -0.5t -0.6t 0.8t 0.4t3 0.5t2 | 6 4t -6 -8t 10 -9t2 8 6t2 -10t 12t2 |
Пример выполнения задачи Д5. Однородная горизонтальная платформа (прямоугольная со сторонами 2l и l), имеющая массу m1, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг оси z с угловой скоростью ω0 (рис. Д5,а). В момент времени t0=0 на вал начинает действовать вращающий момент М, направленный противоположно ω0; одновременно груз D массой m2, находящийся в желобе АВ в точке С, начинает двигаться по желобу (под действием внутренних сил) по закону s=CD=F(t).
Дано: m1 =16 кг, m2=10 кг, l=0,5 м, (s - в метрах, t - в секундах), M=kt, где k =6 Н∙м/с. Определить: ω=f(t) – закон изменения угловой скорости платформы.
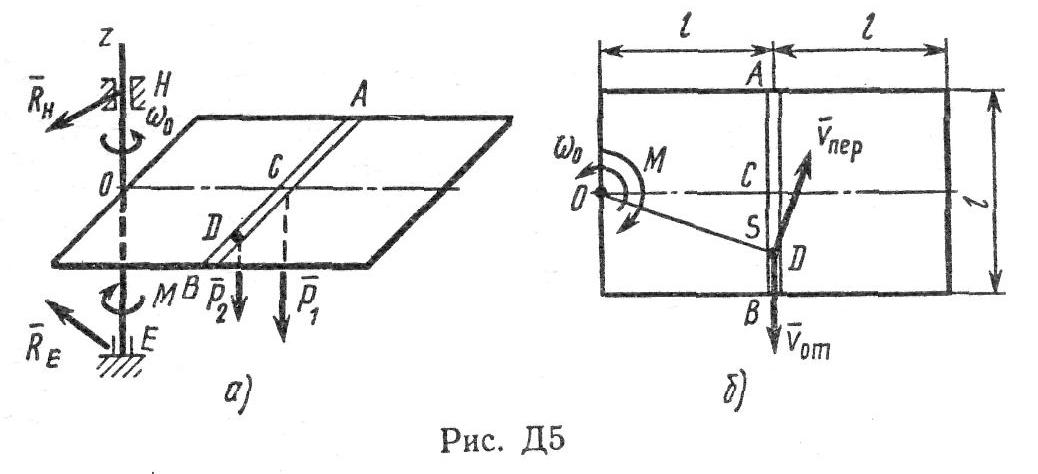
Решение. Рассмотрим механическую систему, состоящую из платформы и груза D. Для определения ω применим теорему об изменении кинетического момента системы относительно оси z:
 . (1)
. (1)
Изобразим действующие на систему внешние силы: силы тяжести  реакции
реакции 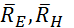 и вращающий момент М. Так как силы
и вращающий момент М. Так как силы 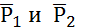 параллельны оси z, а реакции
параллельны оси z, а реакции  эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление ω0 (т.е. против хода часовой стрелки), получим
эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление ω0 (т.е. против хода часовой стрелки), получим 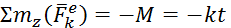 и уравнение (1) примет такой вид:
и уравнение (1) примет такой вид:
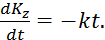 (2)
(2)
Умножая обе части этого уравнения на dt и интегрируя, получим
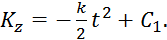 (3)
(3)
Для рассматриваемой механической системы
 , (4)
, (4)
где  и
и 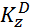 – кинетические моменты платформы и груза D соответственно.
– кинетические моменты платформы и груза D соответственно.
Так как платформа вращается вокруг оси z, то  . Значение
. Значение 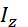 найдем по теореме Гюйгенса:
найдем по теореме Гюйгенса:  (
( - момент инерции относительно оси
- момент инерции относительно оси  , параллельной оси z и проходящей через центр С платформы).
, параллельной оси z и проходящей через центр С платформы).
Но, как известно,

Тогда
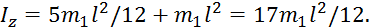
Следовательно,
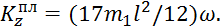 (5)
(5)
Для определения 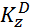 обратимся к рис. Д5,б и рассмотрим движение груза D как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси z переносным движением. Тогда абсолютная скорость груза
обратимся к рис. Д5,б и рассмотрим движение груза D как сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг оси z переносным движением. Тогда абсолютная скорость груза 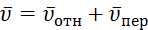 . Так как груз D движется по закону s=CD=0,4t2, то υотн=
. Так как груз D движется по закону s=CD=0,4t2, то υотн= 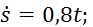 изображаем вектор
изображаем вектор 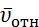 на рис. Д5,б с учетом знака
на рис. Д5,б с учетом знака 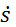 (при
(при 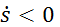 направление
направление 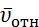 было бы противоположным). Затем, учитывая направление ω, изображаем вектор
было бы противоположным). Затем, учитывая направление ω, изображаем вектор 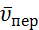 (
( ); численно
); численно 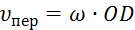 . Тогда, по теореме Вариньона,
. Тогда, по теореме Вариньона,
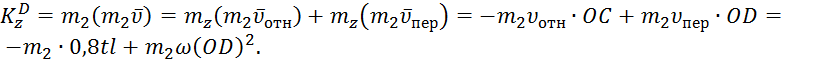 (6)
(6)
Но на рис. Д5,б видно, что 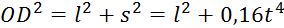 . Подставляя эту величину в равенство (6), а затем значения
. Подставляя эту величину в равенство (6), а затем значения  из (6) и (5) в равенство (4), получим с учетом данных задачи
из (6) и (5) в равенство (4), получим с учетом данных задачи
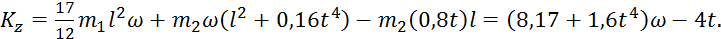 (7)
(7)
Тогда уравнение (3), где k=6, примет вид
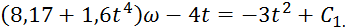 (8)
(8)
Постоянную интегрирования определяем по начальным условиям: при t=0, ω=ω0. Получим 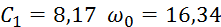 . При этом значении
. При этом значении  из уравнения (8) находим искомую зависимость ω от t.
из уравнения (8) находим искомую зависимость ω от t.
Ответ: 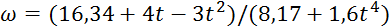 , где t – в секундах, ω – в
, где t – в секундах, ω – в 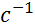 .
.
Контрольные вопросы:
1. Что такое момент количества движения материальной точки?
2. Записать формулу, определяющую момент количества движения точки
3. Сформулировать закон сохранения момента количества движения точки
4. Что такое главный момент количеств движения механической системы?
5. Записать теорему об изменении момента количеств движения точки
6. Записать теорему об изменении главного момента количеств движения механической системы
7. Написать формулу, определяющую момент количества движения твердого тела, вращающегося вокруг неподвижной оси
8. Что такое момент инерции точки?
9. Сформулировать теорему Гюйгенса
10. Что такое главные моменты инерции тела?
Задача Д6
Условие. Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R 3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения p3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 – Д6.9); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено v1, v2, vc5 – скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис.2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д6 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче нужно определить. При вычислении Т для установлении зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика).
При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Таблица Д6
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | c, Н/м | M, Н.м | F=f(s,) Н | Найти |
| 1.2 0.8 1.4 1.8 1.2 1.6 0.8 1.5 1.4 1.6 | 80(4+5s) 50(8+3s) 60(6+5s) 80(5+6s) 40(9+4s) 50(7+8s) 40(8+9s) 60(8+5s) 50(9+2s) 80(6+7s) | ω3 υ1 υ2 ω4 υ1 υC5 ω3 υ2 ω4 υC5 |

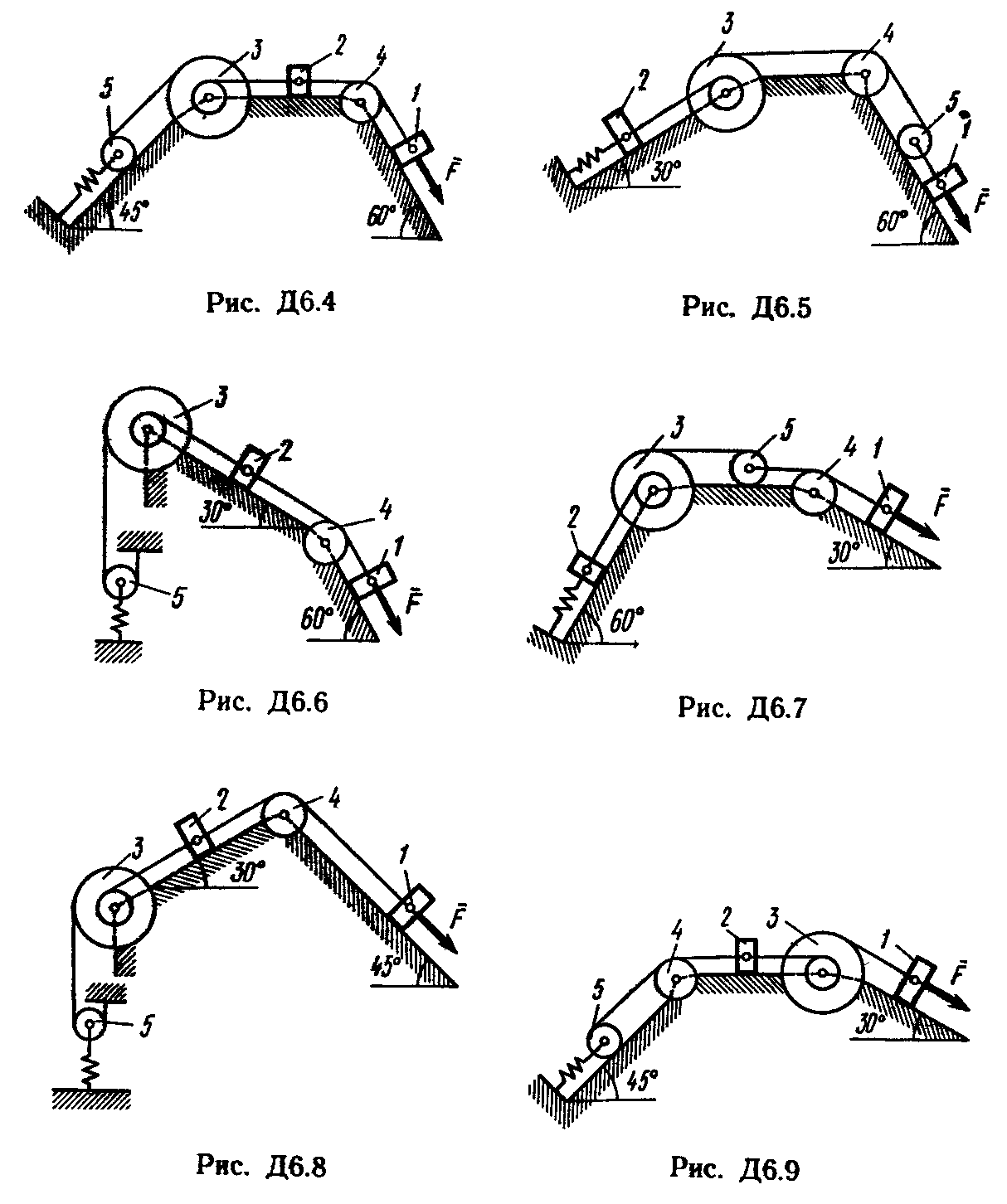
Пример выполнения задачи Д6. Механическая система (рис. Д6,а) состоит из сплошного однородного цилиндрического катка l, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5 (коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю.
Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения точки s ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Дано: 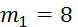 кг,
кг, 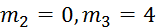 кг,
кг, 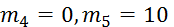 кг, R3=0,3 м, r3=0,1 м, ρ3=0,2 м, f=0,1, c=240 Н/м, M =0,6 Н∙м, F=20(3+2s) H, s1=0,2 м. Определить: ω3 в тот момент времени, когда s=s1.
кг, R3=0,3 м, r3=0,1 м, ρ3=0,2 м, f=0,1, c=240 Н/м, M =0,6 Н∙м, F=20(3+2s) H, s1=0,2 м. Определить: ω3 в тот момент времени, когда s=s1.

Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные 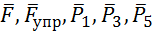 , реакции
, реакции 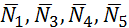 , натяжные нити
, натяжные нити 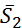 , силы трения
, силы трения 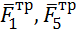 и момент М.
и момент М.
Для определения ω3 воспользуемся теоремой об изменении кинетической энергии:
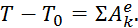 (1)
(1)
2. Определяем 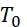 и T. Так как в начальный момент система находилась в покое, то
и T. Так как в начальный момент система находилась в покое, то 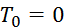 . Величина Т равна сумме энергий всех тел системы:
. Величина Т равна сумме энергий всех тел системы:
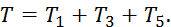 (2)
(2)
Учитывая, что тело l движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим

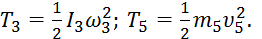 (3)
(3)
Все входящие сюда скорости надо выразить через искомую ω3. Для этого предварительно заметим, что  , где А – любая точка обода радиуса r3 шкива 3 и что точка
, где А – любая точка обода радиуса r3 шкива 3 и что точка 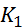 – мгновенный центр скоростей катка l, радиус которого обозначим r1. Тогда
– мгновенный центр скоростей катка l, радиус которого обозначим r1. Тогда
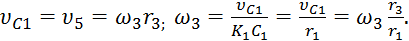 (4)
(4)
Кроме того, входящие в (3) моменты инерции имеют значения
 . (5)
. (5)
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
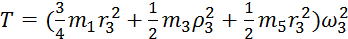 . (6)
. (6)
3. Теперь найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка l пройдет путь 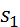 . Введя обозначения:
. Введя обозначения: 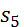 - перемещения груза 5 (
- перемещения груза 5 (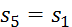 ),
), 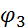 - угол поворота шкива 3,
- угол поворота шкива 3, 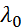 и
и 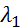 – начальное и конечное удлинение пружины, получим
– начальное и конечное удлинение пружины, получим
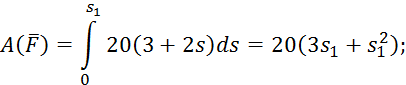
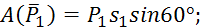
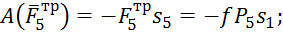

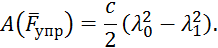
Работы остальных сил равны нулю, так как точки K1 и K 2, где приложены силы 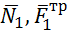 и
и 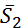 – мгновенные центры скоростей; точки, где приложены силы
– мгновенные центры скоростей; точки, где приложены силы  и
и 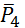 – неподвижны; а реакция
– неподвижны; а реакция 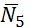 перпендикулярна перемещению груза.
перпендикулярна перемещению груза.
По условиям задачи, 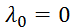 . Тогда
. Тогда 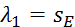 , где
, где  - перемещение точки Е (конца пружины). Величины
- перемещение точки Е (конца пружины). Величины  и
и  надо выразить через заданное перемещение
надо выразить через заданное перемещение 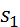 ; для этого учтем, что зависи
; для этого учтем, что зависи