Дифференциальные уравнения первого порядка

 

Дифференциальное уравнение первого порядка есть уравнение вида

F (x, y, y¢) =.

 

Далее мы будем полагать, что это уравнение разрешено относительно производной: y¢=f (x, y). Это уравнение так же можно записать в дифференциальной форме:

 

P (x, y) dx + Q (x, y) dy = 0.

 

Общих методов решения дифференциальных уравнений первого порядка не существует, однако для некоторых важных классов функций f (x,y) такие методы известны и приводят к общему решению уравнения. Рассмотрим некоторые из этих классов.

Уравнения с разделяющимися переменными

 

Так называется уравнение, правая часть которого представляет собой произведение функции, зависящей только от х, и функции, зависящей только от у.

 

 

Для поиска решения такого уравнения выразим входящую в него производную через дифференциалы и перейдем к уравнению в дифференциалах

 

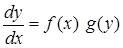
Теперь разделим переменные

 

 

(В последнем уравнении переменные х и у разделяет знак равенства).

Проинтегрировав обе части последнего равенства получаем общее решение уравнения в виде неявно заданной функции:

 

G (y) =F (x) +C.

Рассмотрим практический пример: Найти общее решение уравнения

y' = y cos x.

Решение. Правая часть уравнения представляет собой произведение двух функций, одна из которых зависит от х, а другая от у. Следовательно - это уравнение с разделяющимися переменными. Выразим производную через дифференциалы и разделим переменные:

 

 

Теперь проинтегрируем обе части последнего уравнения:

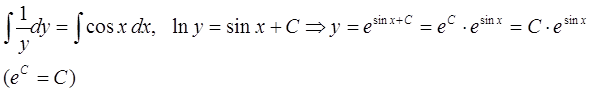
Пример 2. Решить задачу Коши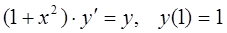

Решение. Сначала найдем общее решение дифференциального уравнения.

 

 

В полученное общее решение подставим заданные начальные условия x=1 и у=1: 0=ln1=acrtg1+С=π /4+С. Значит, частное решение уравнения, удовлетворяющее заданным начальным условиям, получается из его общего решения при значении постоянной С=-π/4. Решением задачи Коши является функция lny=acrtgx-π/4, или y = e ^{arctg x - π / 4.}

Однородные уравнения.

Так называются уравнение вида . С помощью замены переменной z (x) =y (x) /x это уравнение может быть сведено к уравнению с разделяющимися переменными. Действительно, тогда

 

y =x ×z,Þy¢= (x ×z) ¢Þy¢=z xz¢

и для функции z (x) получаем уравнение с разделяющимися переменными

 

Решив это уравнение, найдем функцию z (x), а с ней и решение исходного уравнения y (x) =x z (x).

Пример 1. Найти общее решение уравнения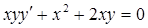

Решение. Разрешим уравнение относительно производной

 

 

и обозначим 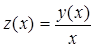. Тогда и для функции z (x) получаем уравнение:

 

 

Это уравнение с разделяющимися переменными.

 

 

Выразим в нем производную через дифференциалы и разделим переменные

 

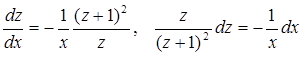
Теперь проинтегрируем обе части последнего уравнения

 

 

Отсюда

 

 

Подставив в последнее равенство z=y/x, найдем общее решение исходного уравнения

Пример 2. Решить задачу Коши

 

Отсюда z = 2arctg (Cx) и, значит, y = 2x × arctg (Cx). Подставив в это

равенство начальные условия x=1 и y = π / 2, получим arctg (C) = π / 4, то есть С=1. Решением задачи Коши является функция y = 2x × arctgx.

Линейные уравнения.

Так называются дифференциальные уравнения вида

y¢p (x) y =q (x).

 

Решение этого уравнения будем искать в виде произведения двух функций y (x) =u (x) v (x). Тогда y¢=u¢v uv¢ и относительно функций u и v уравнение примет вид

u¢v u (v¢p (x) v) =q (x).

 

Вместо одной неизвестной функции y (x) мы ввели в рассмотрение две функции u и v, поэтому одной из них мы можем распорядиться по своему усмотрению. Выберем функцию v так, чтобы слагаемое в скобках в левой части последнего уравнения обращалось в ноль. Для этого в качестве v достаточно взять какое-нибудь решение уравнения с разделяющимися переменными

v¢p (x) v =.

 

Разделяя переменные и интегрируя, получим

 

Таким образом, в качестве v достаточно взять функцию

 

 

При этом мы можем считать, что константа, возникающая в результате вычисления интеграла, равна нулю. При таком выборе функции v для функции u получаем уравнение

 

, или

 

Интегрируя последнее уравнение, получим

 

 

Когда функции u и v найдены, общее решение линейного уравнения находится без труда y=uv.

Уравнение Бернулли.

Естественным обобщением линейного дифференциального уравнения первого порядка является уравнение Бернулли

y¢p (x) y =q (x) y^.

 

Метод его решения таков же, как и метод решения линейного уравнения.