Решение заданий 11 ЕГЭ по информатике

РЕКУРСИВНЫЕ ПРОЦЕДУРЫИ ФУНКЦИИ

Для начала, разберем некоторые определения.

· Процедура (функция) – это вспомогательный алгоритм (фрагмент кода программы), который служит для выполнения определенных действий.

Предназначена для:

o выполнения одинаковых действий в различных местах одной и той же программы;

o разбивки программы (или другой процедуры или функции) на подзадачи для улучшения читаемости кода;

Особенности программирования процедур (функций):

o подпрограммы располагаются всегда выше основной программы:

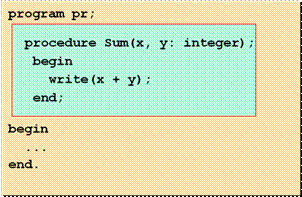
o сначала составляется заголовок процедуры или функции, в котором перечисляются формальные параметры, они обозначаются идентификаторами, как переменные (т.к. формальные параметры могут меняться, также как переменные):

var x,y:integer; { заголовок процедуры с формальными переменными x и y:} procedure Sum(x,y:integer); begin ... end; // основная программа begin ... end.

var x,y:integer; { заголовок функции с формальными переменными x и y:} function Sum(x,y:integer): integer; begin ... end; // основная программа begin ... end.

o в месте вызова процедуры в круглых скобках указываются фактические параметры (числовые значения либо арифметические выражения) в том же порядке:

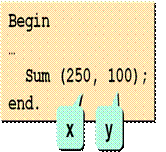
o функция вызывается немного иначе:

{ заголовок процедуры с формальными переменными x и y:} procedure Sum(x,y:integer); begin ... end; // основная программа begin Sum(100,200) end.

{ заголовок функции с формальными переменными x и y:} function Sum(x,y:integer): integer; begin ... end; // основная программа begin write (Sum(100,200)) end.

o компилятор не будет выполнять процедуру (функцию) до момента ее вызова в основной программе;

o пример работы процедуры и функции для сложения двух значений (порядок действий компилятора указан числами):

var x,y:integer; procedure Sum(x,y:integer); begin //3. Выводим сумму двух запрошенных чисел write(x+y); end; begin // 1. запрашиваем два числа readln(x,y); // 2. передаем запрошенные числа в процедуру Sum(x,y) end.

var x,y:integer; function Sum(x,y:integer): integer; begin {3. Суммируем два числа и присваиваем значение функции:} Sum:=x+y; end; begin // 1. запрашиваем два числа readln(x,y); {2. передаем запрошенные числа в функцию и выводим результат:} write (Sum(x,y)) end.

Подробное описание работы с процедурами можно найти, перейдя по ссылке.

o Рекурсивной называется процедура, вызывающая сама себя:

procedure row(n:integer); begin if n >=1 then begin write (n, ' '); row(n-1) end; end; begin row(10); end.

Для использования рекурсии, необходимо задать:

· условие остановки рекурсии (обычно, в виде условного оператора):

if n >=1 then begin

· рекуррентную формулу (обычно, вызов самой себя с измененным параметром):

row(n-1)

Подробное описание работы с рекурсивными процедурами и функциями в Паскале можно найти здесь.

Решение заданий 11 ЕГЭ по информатике

 

11_1: Решение задания 11 (Поляков К., вариант 2):

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * (n + 2), при n > 1

Чему равно значение функции F(5)? В ответе запишите только целое число.

Решение:

Метод решения с конца к началу:

· Из условия задания мы имеем рекуррентную формулу: F(n–1) * (n + 2) и условие остановки рекурсии: n > 1.

· Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 5:

F(5) = F(4) * 7

· Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(1) (при котором «сработает» остановка рекурсии). Получим:

F(5) = F(4) * 7

F(4) = F(3) * 6

F(3) = F(2) * 5

F(2) = F(1) * 4

· На F(2) необходимо остановиться, так как действует условие остановки рекурсии: формула работает для n > 1. Также учтем, что по условию F(1) = 1.

· Теперь с конца к началу перепишем все получившиеся сомножители и перемножим их:

1 * 4 * 5 * 6 * 7 = 840

Результат: 840

11_2: Решение задания 11 (Поляков К., вариант 7):

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(0) = 1, F(1) = 1

F(n) = 2 * F(n–1) + F(n-2), при n > 1

Чему равно значение функции F(6)? В ответе запишите только целое число.

Решение:

✎ Решение 1. Метод решения с начала к концу:

· Из условия задания мы имеем рекуррентную формулу: 2 * F(n–1) + F(n-2) и условие остановки рекурсии: n > 1.

· Из заданной рекуррентной формулы видим, что функция зависит от предыдущей функции (F(n–1)) и от пред-предыдущей функции (F(n-2)).

· Так как первые два значения заданы (F(0) = 1, F(1) = 1), то можно построить таблицу последующих значений, двигаясь к числу 6:

n
F(n) 2*F(n – 1)+F(n — 2)			2*1+1 =3	2*3+1 =7	2*7+3 =17	2*17+7 =41	2*41+17 =99

· Таким образом, получаем, что при вызове функции F(6) результатом будет число 99

✎ Решение 2. Метод решения с конца к началу:

· Поскольку рекуррентная формула уже задана, то остается подставить в нее начальный параметр — число 6:

F(6) = 2*F(5) + F(4)

· Теперь применим эту формулу для всех вызываемых вложенных функций, вплоть до F(2) (F(1) и F(0) известны из условия задачи). Получим:

F(6) = 2*F(5) + F(4)

F(5) = 2*F(4) + F(3)

F(4) = 2*F(3) + F(2)

F(3) = 2*F(2) + F(1)

F(2) = 2*F(1) + F(0) = 2*1+1 = 3

1 1

· Теперь с конца к началу перепишем все получившиеся значения функций:

F(6) = 2*F(5) + F(4) = 2*41 + 17 = 99

F(5) = 2*F(4) + F(3) + 2*17+7 = 41 ↑

F(4) = 2*F(3) + F(2) = 2*7+3 = 17 ↑

F(3) = 2*F(2) + F(1) = 2*3+1 = 7 ↑

F(2) = 2*F(1) + F(0) = 2*1+1 = 3 ↑

1 1

Результат: 99

Решение данного задания 11 также можно посмотреть в видеоуроке:

11_3: ЕГЭ по информатике 2017 задание 11 ФИПИ вариант 2 (Крылов С.С., Чуркина Т.Е.):

Ниже записаны две рекурсивные функции (процедуры): F и G.
Сколько символов «звездочка» будет напечатано на экране при выполнении вызова F(18)?

Паскаль:

	procedure F(n: integer); forward; procedure G(n: integer); forward;   procedure F(n: integer); begin write('*'); if n > 10 then F(n - 2) else G(n); end;   procedure G(n: integer); begin write('**'); if n > 0 then F(n - 3); end;
Бейсик: DECLARE SUB F(n) DECLARE SUB G(n) SUB F(n) PRINT "*" IF n > 10 THEN F(n - 2) ELSE G(n) END IF END SUB SUBG(n) PRINT "**" IF n > 0 THEN F(n - 3) END IF END SUB	Python: def F(n): print("*") if n > 10: F(n - 2) else: G(n) def G(n): print("**") if n > 0: F(n - 3)
С++: void F(int n) { std::cout << "*"; if (n > 10) { F(n - 2); } else { G(n); } } void G(int n) { std::cout << "**"; if (n > 0) F(n - 3); }

Типовые задания для тренировки

Решение:

· Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:

*

F(n - 2) при n > 10

G(n) при n <= 10

 

Для G:

**

F(n - 3) при n > 0

✎ Способ 1:

· Выпишем последовательность вызовов процедур, начиная с указанного в задании F(18):

F(18) -> F(16) -> F(14) -> F(12) -> F(10) -> G(10) ->

F(7) -> G(7) -> F(4) -> G(4) -> F(1) -> G(1) -> F(-2) -> G(-2)

· Обратим внимание, что независимо от условия процедура F выводит на экран одну *, а процедура G выводит две *. Посчитаем для последовательности вызовов итоговую сумму звездочек: 9F + 5G = 9*1 + 5*2 = 19

Результат: 19

✎ Способ 2:

· Рассмотрим пошагово выполнение программы при вызове F(18):

1 шаг: F(18)

* F(16)

2 шаг: * F(14)

3 шаг: * F(12)

4 шаг: * F(10)

5 шаг: * G(10)

6 шаг: ** F(7)

7 шаг: * G(7)

8 шаг: ** F(4)

9 шаг: * G(4)

10 шаг: ** F(1)

11 шаг: * G(1)

12 шаг: ** F(-2)

13 шаг: * G(-2)

14 шаг: **

· Посчитаем количество звездочек: 19

Результат: 19

Пошаговое решение данного 11 задания ЕГЭ по информатике доступно в видеоуроке:

11_4: ЕГЭ по информатике «Типовые экзаменационные варианты» 2019, ФИПИ, ВАРИАНТ 10 (Крылов С.С., Чуркина Т.Е.):

Ниже записаны две рекурсивные функции (процедуры): F и G.
Какова сумма чисел, напечатанных на экране при выполнении вызова F(17)?

Паскаль:

	procedure F(n: integer); forward; procedure G(n: integer); forward;   procedure F(n: integer); begin writeln(n); if n mod 2 =0 then F(n div 2) else G((n - 1) div 2); end;   procedure G(n: integer); begin writeln (n); if n > 0 then F(n); end;
Бейсик: DECLARE SUB F(n) DECLARE SUB G(n) SUB F(n) PRINT n IF n MOD 2 = 0 THEN F(n \ 2) ELSE G ((n - 1) \ 2) END IF END SUB SUBG(n) PRINT n IF n > 0 THEN F(n) END IF END SUB	Python: def F(n): print(n) if n % 2 == 0: F(n // 2) else: G((n - 1) // 2) def G(n): print(n) if n > 0: F(n)
С++: void F(int n) { std::cout << n << endl; if (n % 2 == 0) { F(n / 2); } else { G((n - 1) / 2); } } void G(int n) { std::cout << n << endl; if (n > 0) F(n); }

Типовые задания для тренировки

Решение:

· Для удобства восприятия задания, выпишем рекуррентные формулы и условия остановки рекурсии для двух процедур:

Для F:

n

F(n div 2) при n - четное (n mod 2 = 0)

G((n - 1) div 2) при n - нечетное

 

Для G:

n

F(n) при n > 0

· Выпишем последовательность вызовов процедур, начиная с указанного в задании F(17).

· Обратим внимание, что независимо от условия как процедура F выводит на экран n, так и процедура G выводит n.

F(17) -> n - нечетное, G(8) вывод 17

G(8) -> F(8) вывод 8

F(8) -> n - четное, F(4) вывод 8

F(4) -> n - четное, F(2) вывод 4

F(2) -> n - четное, F(1) вывод 2

F(1) -> n - нечетное, G(0) вывод 1

G(0) вывод 0

· Сумма:

17 + 8 + 8 + 4 + 2 + 1 + 0 = 40

Результат: 40

11_5, Источник: Поляков К, ВАРИАНТ 77

Ниже записаны две рекурсивные функции (процедуры): F и G.
Чему будет равно значение, вычисленное при выполнении вызова F(6)?

Паскаль:

	function F(n: integer):integer; forward; function G(n: integer):integer; forward; function F(n:integer):integer; begin if (n > 2) then F:= F(n - 1) + G(n - 2) else F:= n; end; function G(n:integer):integer; begin if (n > 2)then G:= G(n - 1) + F(n -2) else G:= n+1; end;
Бейсик: FUNCTION F(n) IF n > 2 THEN F = F(n - 1) + G(n - 2) ELSE F = n; END IF END FUNCTION FUNCTION G(n) IF n > 2 THEN G = G(n - 1) + F(n -2) ELSE G = n+1; END IF END FUNCTION	Python: def F(n): if n > 2: return F(n - 1) + G(n - 2) else: return n def G(n): if n > 2: return G(n - 1) + F(n - 2) else: return n+1
С++: int F(int n); int G(int n); int F(int n) { if (n > 2) return F(n - 1) + G(n - 2); else return n; } int G(int n) { if (n > 2) return G(n - 1) + F(n - 2); else return n + 1; }

Типовые задания для тренировки

Решение:

Результат: 17

Предлагаем посмотреть видеоразбор данного решения:

11_6: 11 задание. Демоверсия ЕГЭ 2018 информатика:

Ниже на пяти языках программирования записан рекурсивный алгоритм F.
Паскаль:

	procedure F(n: integer); begin if n > 0 then begin write(n); F(n - 3); F(n div 3) end end;
Бейсик: SUB F(n) IF n > 0 THEN PRINT n F(n - 3) F(n \ 3) END IF END SUB	Python: def F(n): if n > 0: print(n) F(n - 3) F(n // 3)	С++: void F(int n){ if (n > 0){ std::cout <<n; F(n - 3); F(n / 3); } }

Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(9). Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Решение:

Рассмотрим алгоритм:

· В данном фрагменте программы рекурсивная процедура вызывает саму себя дважды.

· Благодаря условию, находящемуся в процедуре (if n > 0 — условие остановки рекурсии), обеспечивается выход из рекурсии и не происходит «зацикливания».

· Выполнение процедур закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 0 перестанет работать (т.е. когда параметр процедуры n станет <= 0).

· div — целочисленное деление, т.е., например:

5 div 2 = 2

1 div 2 = 0

· Отобразим пошагово выполнение каждой процедуры, двигаясь сверху вниз и оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

F(9)

1: 9 F(6) (9 - 3 = 6)

2: 6 F(3) (6 - 3 = 3)

3: 3 F(0) (3 - 3 = 0, условие не работает)

4: F(1) (3 div 3 = 1)

5: 1 F(-2) (1 - 3 = -2, условие не работает)

6: F(0) (1 div 3 = 0, условие не работает)

7: F(2) (6 div 3 = 2)

8: 2 F(-1) (2 - 3 = -1, условие не работает)

9: F(0) (2 div 3 = 0, условие не работает)

10:F(3) (9 div 3 = 3)

11:3 F(0) (3 - 3 = 0, условие не работает)

12:F(1) (3 div 3 = 1)

13: 1 F(-2) (1 - 3 = -2, условие не работает)

· Выделены те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.

· Перепишем по порядку все выводимые на экран числа сверху вниз: 9631231

Результат: 9631231

11_7: Решение задания 11 Информатика и ИКТ 2019 3 вариант (Крылов С.С, Чуркина Т.Е., 10 вариантов):

Ниже записан рекурсивный алгоритм F. Запишите подряд без пробелов и разделителей все числа, которые будут напечатаны на экране при выполнении вызова F(130).
Числа должны быть записаны в том же порядке, в котором они выводятся на экран.

Паскаль:

	procedure F(n: integer); begin if n > 1 then begin write(n); F(n div 10); F(n - 40) end end;
Бейсик: SUB F(n) IF n > 1 THEN PRINT n F(n \ 10) F(n - 40) END IF END SUB	Python: def F(n): if n > 1: print(n) F(n // 10) F(n - 40)	С++: void F(int n){ if (n > 1){ std::cout <<n; F(n / 10); F(n - 40); } }

Решение:

Разберем алгоритм программы:

· В данном фрагменте программы рекурсивная процедура F вызывает саму себя дважды.

· В процедуре находится условие if n > 1 — условие остановки рекурсии, благодаря которому обеспечивается выход из рекурсии и не происходит «зацикливания».

· Выполнение фрагмента программы закончится, когда в каждой из вызванных процедур выполнятся по две внутренние процедуры, и условие if n > 1 перестанет работать (т.е. когда параметр процедуры n станет <= 1).

· div — целочисленное деление, т.е., например:

5 div 3 = 1

1 div 3 = 0

· Выполним трассировку кода процедуры: двигаться будем пошагово сверху вниз, оставляя отступы слева с каждым новым шагом. В каждой строке будем отображать порядковый номер шага. Под вызовом каждой процедуры разместим именно те действия, которые происходят в данной процедуре:

F(130) 130

1: ➥ F(13) (130 div 10 = 13) 13

2: ➥ F(1) условие не работает! 1 ≤ 0

3: ➥ F(-27) условие не работает! -27 ≤ 0

4: ➥ F(90) (130 - 40 = 90) 90

5: ➥ F(9) (90 div 10 = 9) 9

6: ➥ F(0) условие не работает! 0 ≤ 0

7: ➥ F(-31) условие не работает! -31 ≤ 0

8: ➥ F(50) (90 - 40 = 50) 50

9: ➥ F(5) (50 div 10 = 5) 5

10: ➥ F(0) условие не работает! 0 ≤ 0

11: ➥ F(-35) условие не работает! -35 ≤ 0

12: ➥ F(10) (50 - 40 = 10) 10

13: ➥ F(1) условие не работает! 1 ≤ 0

14: ➥ F(-30) условие не работает! -30 ≤ 0

· Выделены красным цветом те числа, которые выводятся на экран. Подчеркнуты те процедуры, в которых условие не работает, соответственно, ничего на экран не выводится.

· Перепишем сверху вниз все выводимые на экран числа: 1301390950510

Результат: 1301390950510

11_8: Решение задания 11 (Поляков К., вариант 78):

Вызов представленной ниже рекурсивной функции приводит к появлению на экране чисел и точек. С каким минимальным натуральным аргументом а нужно вызвать эту функцию, чтобы в результате на экране появилось 5 точек (не обязательно подряд, между точками могут встречаться числа)?
Паскаль:

function gz(a:integer):integer; var p:integer; begin if a<1 then begin gz:=1; exit; end; if a mod 3=0 then begin write('...'); p:=gz(a div 3)+gz(a div 4); end else begin write('.'); p:=gz(a div 4); end; write(p); gz:=2; end;

Решение:

Результат: 6

: