Метод штрафных функций и его применение для оптимизационных задачах.
Решение систем линейных уравнений относительно неопределённых множителей не всегда оправданно, так как эти множители не всегда исключаются.
Для исключения этих трудностей используют следующий метод.
Для этого оптимизационное решение может выходить в недопустимую область. Этот выход в область регулируется добавкой к целевой функции и чем больше нарушение ограничений, тем больше добавка именуемая штрафной.
Пусть штрафная функция именуется глобальной штрафной, которая в свою очередь находится в недопустимой области (рисунок 1).
Пусть имеется целевая функция глобального штрафа наибольший экстремум которой находится в недопустимой области. Допустимое решение т. 2 находящаяся на границе.
Рисунок 1
Функция штрафа записывается: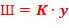 
.
Данная функция предназначена для уменьшения целевой функции. При нарушении условия дифференцировании функции наиболее благоприятно, когда штрафная функция (Ш) имеет вид квадратичной функции: 
.
В точке излома дифференциальная функция отсутствует, т.е. сохраняется свойство дифференцируемости функции.
Рост, штрафного элемента приближает т. 
к целевой функции экстремума т. 2.
Из-за слишком большой величины функции при переходе 
, происходит деформирование исходной функции, заменяя задачу её минимизации, задачей минимизирования штрафной функции.
Подбор веса этой функции выявляется в процессе решения задачи.
Пример:
Исходная задача вида:
,
, 
.
.
где 
– это функция ограничения.
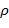– весовой коэффициент задания. Не является предметом оптимизации.
Данная функция ограничения должна образовывать штрафную добавку.
Для сглаживания функции, применяются квадратичные уравнения.
Найти наилучшее распределение мощности между источниками, методом штрафных функций.
Получаем функцию с учётом штрафной добавки 
:
;
;
; 
Увеличим влияние штрафной функции 
Тогда получим следующую функцию:
=33,22;
=66,50;
Решение допустимое.
Методы одномерной оптимизации в алгоритмах задач МП. Общий подход к определению оптимального шага.
Решение оптимизационных задач в общем случае – это итерационная процедура в результате которой отыскивается минимум целевой функции. При этом необходимо задать правило (закон) изменения итерационных переменных в соответствии с общепринятой формулой.
,
,
где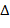 
– это направление изменения переменных,
– это шаг по указанному направлению.
Поиск представляет собой самостоятельную задачу, основанную на идеях, подходах одномерного поиска.
Непосредственное определение оптимального шага на основе общего подхода.
На начальном этапе необходимо знать интервал на котором находится экстремум функции.
Для функции одной переменной внутри интервала, функция непрерывна и дифференцируема.
Направление изменения переменных связанно с изменением координат оси. Необходимо найти величину шага, который приведёт к экстремуму (рисунок 2).
Рисунок 2
,
Представим, что функция имеет аналогичный и не сложный вид:
,
Пусть имеем начальное значение переменных 
и начальное значение интервала локализации функции .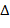
Выразим функцию в явном виде от шага:
,
Воспользовавшись экстремумом, получим:
. (1)
Решая это уравнение получим наилучшее значение шага на предыдущем значении функции.
Пусть 
, тогда при a=2, b=3, c=4 начальное значение будет:
.
Пусть известно 
, выразим функцию в явном виде от шага.
Решая выражение (1) с первой независимой:
.
Далее получим значение функции с этим шагом:
.
.
Представим функцию двух переменных:
.
Решая данное уравнение выше, получим оптимальный шаг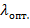 
перемещения с которым в заданном направлении даст 
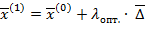координаты минимума функции.
Из этого следует, что определение шага возможно для тривиальной функции.
Для функции отличающейся от тривиальной определение шага затрудненно.
Трансындентная функция: 
. Такой общий подход является трудно реализуемым.