Структурная группа (группа Ассура)
Структурная группа (группа Ассура) – это такая кинематическая цепь, присоединение которой к любому механизму не изменяет его числа степеней свободы. При этом такая цепь не должна распадаться на более простые цепи с тем же свойством. Так как группа Ассура не изменяет числа степеней свободы механизма после присоединения к нему или отсоединения от него, то она обладает собственной нулевой степенью свободы. Таким образом:Wгр=3nгр–2p5гр=0, откуда p5гр=3nгр/2 или nгр=2p5гр/3,где: nгр – число звеньев в группе Ассура, включая фиктивные звенья, полученные при замене высших пар, p5гр – число кинематических пар пятого класса в группе Ассура, включая пары, полученные при замене высших пар. Примечание: рассматриваются структурные группы, включающие только низшие пары 5 класса, т.к. при наличии высших кинематических пар в механизме их можно заменить цепями с низшими парами. Так как количество звеньев и кинематических пар заведомо целые числа, то число звеньев в группе Ассура всегда четное, а число кинематических пар кратно трем. Таким образом группы Ассура имеют следующие сочетания чисел звеньев и кинематических пар (таблица 2.1). Класс группы Ассура определяется числом сторон замкнутого контура (многоугольника), входящего в состав этой группы. При этом все группы, имеющие два звена, относятся к группам II класса, а контур с числом сторон больше трех должен быть подвижным (т.е. иметь изменяемую форму при работе механизма). Порядок группы Ассура Порядок группы Ассура определяется числом элементов кинематических пар, которыми группа присоединяется к механизму.Группы Ассура второго класса одновременно являются группами второго порядка (иногда их называют двухповодковыми группами), но они еще подразделяются на виды. Вид группы Ассура зависит от сочетания вращательных (шарниров) и поступательных (ползунов) кинематических пар в данной группе. Всего существует пять видов групп Ассура второго класса.
8. Понятие о степени подвижности механизма
Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p1,p2,… p5, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.
W=6n-5p5-4p4-3p3-2p2-p1 (3.1)
Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.
Для плоского механизма степень подвижности определяется по формуле Чебышева: W=3n-2p5-p4, (3.2)
При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма (рис.8).
а) W=3·4-2·6-0=0 – с пассивным звеном,
б) W=3·3-2·4-0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей,
Формула П. Л. Чебышева для плоских механизмов
Для плоского механизма используется формула Чебышева:
W=3n-1P4-2P5
где n-число подвижных звеньев
P4,P5-кинематические пары с одной и с двумя наложенными связями.
По-другому эту формулу можно записать в следующем виде:
W=3n-2Pн-Pв
где n-общее число подвижных звеньев механизма
Рн - число низших кинематических пар
Рв — число высших кинематических пар
10. Кинематический анализ механизмов заключается в исследовании движения звеньев механизмов независимо от сил, вызывающих это движение. В результате этого анализа определяются положения звеньев и траектории отдельных точек звеньев; линейные скорости отдельных точек и угловые скорости звеньев; линейные ускорения отдельных точек и угловые ускорения звеньев. [ 1 ]
Кинематический анализ механизмов может выполняться аналитическими и графическими методами. [ 2 ]
Кинематический анализ механизма ведется в следующем порядке: сначала исследуется движение начальных звеньев, а затем выполняется кинематический анализ отдельных структурных групп в порядке их присоединения при образовании механизма. В этом случае в каждой структурной группе будут известны положения, скорости и ускорения тех элементов кинематических пар, к которым присоединяется данная группа. Кинематический анализ каждой группы Ассура должен начинаться с определения кинематических параметров внутренних пар группы. [ 3 ]
Кинематический анализ механизмов в общем случае предусматривает решение трех основных задач, а именно: 1) определение положений звеньев и построение траекторий отдельных точек; 2) определение скоростей точек и угловых скоростей звеньев; 3) определение ускорений точек и угловых ускорений звеньев. [ 4 ]
Кинематический анализ механизма заключается в определении линейных скоростей и ускорений точек и угловых скоростей и угловых ускорений звеньев. Закон изменения этих величин часто нужно знать для составления характеристики работы механизма, а в некоторых случаях - для дальнейших расчетов. [ 5 ]
Провестикинематический анализ механизма - - это значит по заданной кинематической схеме механизма найти и исследовать функции, описывающие перемещения, скорости и ускорения отдельных точек механизма при известном законе движения ведущих звеньев. Аналитическое исследование кинематики часто наталкивается на математические трудности. Так, аналитический вид траекторий некоторых точек простейших механизмов с одной степенью свободы представляется алгебраическими уравнениям. Поэтому в теории механизмов и машин подучили широкое распространение различного рода графические методы анализа кинематики. [ 9 ]
11. Метод планов скоростей и ускорений
Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов.
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное - движение данной точки относительно той, движение которой принято за переносное:
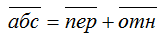
Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

Планы скоростей и ускорений обладают следующими свойствами:
- на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;
- отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;
- фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;
- имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.
При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:
1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).
В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей
Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С1, принадлежащей этой направляющей.
Движение точки С1 принимается в качестве переносного. Движение точки С2, принадлежащей ползуну, относительно точки С1 получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С1 и С2 совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).
Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.