Уравнение Пуассона:
, (#1)
где
– оператор Лапласа (#2)
Заметим, что оператор Лапласа часто обозначается символом 
, т.е. равнозначны все три формулировки оператора Лапласа:
(#3)
#1. Общий вид формулировки краевой задачи для уравнения Пуассона.
Пусть краевая задача рассматривается в некоторой области W с границей 
(рис. #1).
Рис. #1. Пример области, на которой рассматривается задача Пуассона.
Пусть 
– вектор нормали к границе области 
,
; 
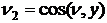. (#4)
В зависимости от условий на краях области (краевых условий) краевая задача может иметь разные названия. В частности:
– задача Дирихле (первая краевая задача):
(#5)
– задача Неймана (вторая краевая задача):
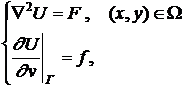(#6)
где
– производная по нормали. (#7)
Если на одной части границы заданы условия задачи Дирихле, а на другой – условия задачи Неймана, тогда таким образом сформулированная краевая задача называется смешанной краевой задачей.
#2. Решение задачи Дирихле методом конечных разностей.
Рассмотрим задачу Дирихле в прямоугольной области (рис. #2). Тогда ее математическую формулировку можно представить в виде:
(#8)
Здесь все величины заданы, кроме функции 
(искомая функция).
Заметим, что при решении задачи на ЭВМ естественным является задание направления оси 
вниз, поскольку это соответствует естественному порядку вывода (печати) на экран или принтер (вывод информации последовательно сверху вниз). Это особенно важно при «промежуточной» печати во время счета.
Рис. #2. Прямоугольная область, на которой рассматривается задача Дирихле.
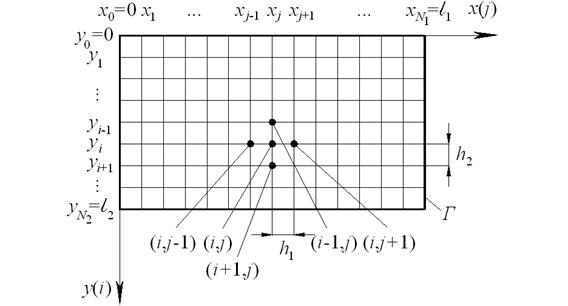
Рис. #3. Дискретизация рассматриваемой области.
Разобьем исходную прямоугольную область на мелкие прямоугольники с помощью сетки с постоянным шагом 
по первому направлению (по координате 
) и с постоянным шагом 
– по второму направлению (по координате 
):
|
|
; 
, (#9)
где 
и 
– число узлов сетки по 1-му и 2-му направлению, соответственно (рис. #3).
Будем рассматривать задачу (#8) в узлах сетки – в точках пересечения линий разбиения области. Каждый узел сетки имеет номер, определяемый двумя величинами 
, где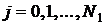 
– номер узла по направлению оси , 
– номер узла по направлению оси .
Введем обозначения:
; 
; 
. (#10)
Вторые производные для внутренних узлов сетки по каждому направлению заменим вторыми разностями, т.е.
; 
. (#11)
Тогда краевая задача в конечных разностях примет вид:
– для внутренних узлов:
, 
, 
; (#12)
– для граничных узлов:
(#13)
Итак, для определения 
во внутренних точках достаточно решить систему из 
уравнений c неизвестными, используя заданные значения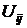 
на границе.
С алгоритмической точки зрения наиболее простыми способами решения такой системы являются итерационные, в частности, метод Зейделя и метод простой итерации. Для этого, выделив из уравнений (#12) диагональный член 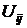, получим:
. (#14)
Далее, задав начальное приближение 
для внутренних точек и присвоив заданные значения 
для граничных точек, реализуем алгоритм метода Зейделя в виде
(#15)
, 
, 
.
Здесь и в дальнейшем – номер итерации.
Счет ведется до тех пор, пока не будет выполнено условие
, (#16)
где 
– заданная точность; 
– оценка погрешности на 
-м шаге итерации.
Заметим, что сходимость метода Зейделя для задач такого типа доказывается в более подробных курсах вычислительной математики. Она следует из, так называемой, положительной определенности оператора (матрицы) краевой задачи. Отметим, что в данном случае диагонального преобладания в матрице нет (и не требуется).
|
|