Арифметические свойства производной.

Билет 1

Производная. Определение, непрерывность функции, имеющей производную.

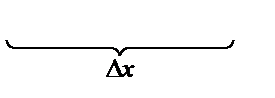
Определение: Производной от функции 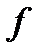в точке называется предел, к которому стремится отношение ее приращения 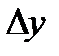в этой точке к соответствующему приращению 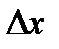аргумента, когда последнее стремится к нулю:

Т.е., если определена в 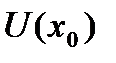, то

Теорема: (необходимое условие существования производной)

Если функция 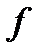имеет конечную в точке , то 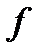непрерывна в точке .

Доказательство:

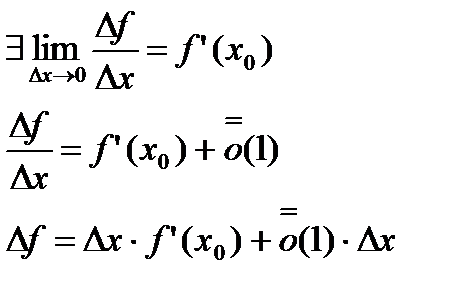
При ,

Следовательно 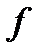- непрерывна в точке .

Теорема доказана.

 

Замечание: обратное утверждение неверно, если функция 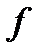непрерывна в точке , то отсюда не следует, что она имеет производную в этой точке.

Контрпример:

Утверждение: если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева.

Контрпример:

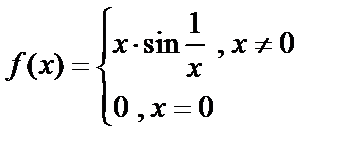
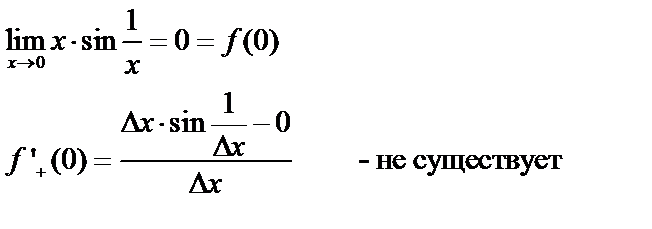
Билет 2Геометрический смысл производной.

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

A

B

C

Доказательство:

Пусть существует значение f’(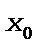)-конечное, тогда

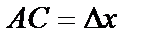
при

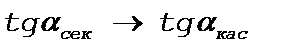
Секущая стремится к касательной.

=> ч.т.д.

Пусть существует невертикальная касательная => существует 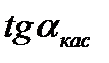- конечный.

Секущая стремится к касательной.

=>

Теорема доказана.

Производные элементарных функций.

1. ;

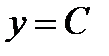2.

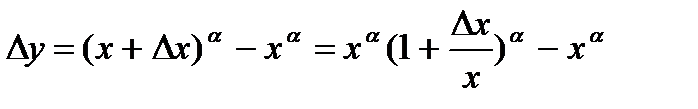
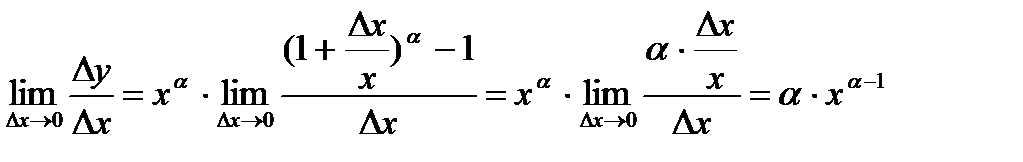
3.

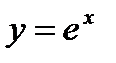
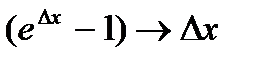
4.

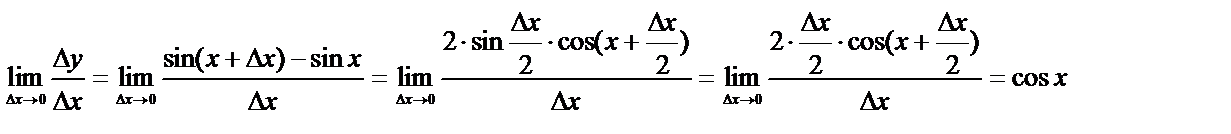(т.к. функция непрерывна)

Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке (было доказано в Билете 1), но она может быть разрывной в любой другой точке, кроме этой.

Пример:

, т.к.

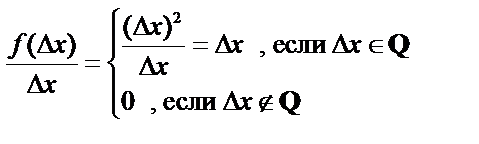
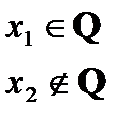
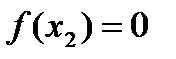
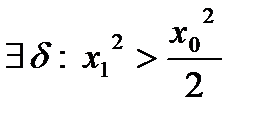
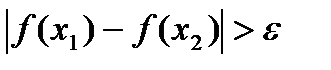- не выполняется критерий Коши и в каждой точке функция разрывна.

Билет 3

Арифметические свойства производной.

Пусть f = f(x) и g = g(x) – функции, имеющие конечные производные в точке x₀, тогда справедливы равенства:

1.

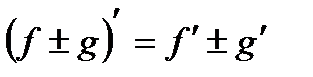
2.

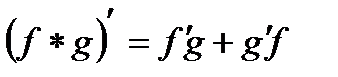
2.1. 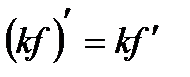где k – константа

3.

-----------------------------------------------------------------------------------------------------------------------------

1.

 

2.

Заметим, что функция f, как имеющая производную, непрерывна, и потому при

 

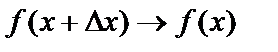
3.

Точка перегиба. Достаточные условия. Общая теорема о точках перегиба и экстремума.

Определение. Точка 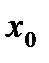называется точкой перегиба, если в этой точке график переходит через сторону касательной (разные выпуклости слева и справа).

Замечание. Точка перегиба существует только если . Пример

Теорема 1 (Достаточное условие существования точки перегиба).

Если функция 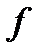имеет непрерывной в точке , =0 и , то 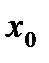точка перегиба.

Доказательство: В этом случае: , 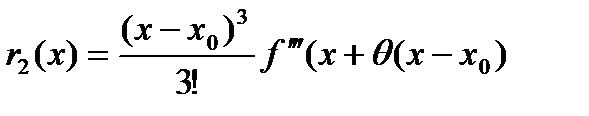(формула Тейлора), или .

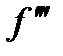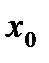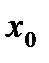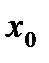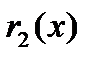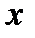В силу непрерывности в и того факта, что сохраняет знак в некоторой окрестности точки . С другой стороны, множитель меняет знак при переходе через , а вместе с ним и величина (равная превышению точки кривой над касательной в ) меняет знак при переходе через .

Теорема доказана.

Теорема 2 (Общая теорема о точках перегиба и экстремума.)

Пусть функция 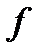обладает следующими свойствами:

непрерывна в и . Тогда, если - нечетное число, то кривая 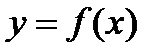обращена выпуклостью вверх или вниз в зависимости от того, будет ли или , а если четное, то 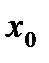есть точка перегиба кривой.

Доказательство:

Разложим по формуле Тейлора:

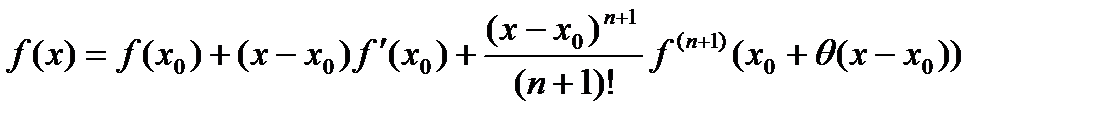
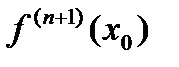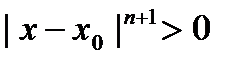того же знака, что , , , если - четное то

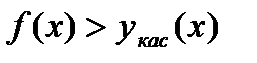или всегда, - не точка перегиба.

Если - нечетная

С одной стороны 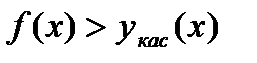, с другой стороны - точка перегиба. - четное.

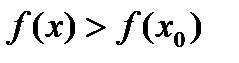, - min

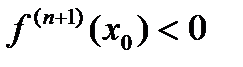, - max

Билет 22