Для определения вероятности (частоты) наступления ущерба используют как отдельно, так и в совокупности:
- статистические данные;
- метод логического анализа дерева событий, представленный на рисунке Б.1;
- метод вербальных функций;
- экспертную оценку специалистов в данной области.
Рисунок Б.1 - Дерево событий. Схема расчета вероятности наступления ущерба
При проведении логического анализа дерева событий за первоначальное событие принимают факт наличия опасности (например, шума, открытого огня, использования на рабочем месте сосудов, работающих под давлением, и т.д.). Такое событие отображают в виде узла на верхнем уровне (см. рисунок Б.1). Одной опасности соответствует один узел на верхнем уровне. Всего может быть идентифицировано 
опасностей.
Последующие события (возможные проявления опасностей) при необходимости размещают на втором уровне дерева событий. Например, опасность "открытый огонь" (узел 1) может проявиться в виде пожара (узел 1.1), задымленности (узел 1.2), повышенной температуры (узел 1.3) и т.д.
Каждая 
-я ветвь дерева из общего их числа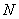 
представляет собой определенный -й сценарий наступления последствий проявления опасности. Вероятность реализации -го сценария 
- условная вероятность конечного в ветви события. Наступление последствий по -му сценарию приводит к возникновению того или иного ущерба 
.
Для каждого уровня дерева событий определяют вероятности (частоты) наступления возможных ущербов, вызванных идентифицированными опасностями, и исхода, не связанного с наступлением ущерба. При этом указанные события на каждом уровне должны составлять полную группу событий (сумма вероятностей (частот) их наступления должна равняться единице).
|
|
Путем перемножения вероятностей по ветвям дерева событий определяют вероятности 
, 
,..., наступления ущербов 
, 
,..., и вероятность исхода, не связанного с наступлением ущерба.
Метод логического анализа дерева событий может быть применен в сочетании с вербальным описанием вероятностей (частот) наступления ущерба. При этом возможным качественным значениям вероятностей (частот) наступления ущерба , ,..., 
присваивают весовые коэффициенты 
, 
,..., 
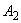соответственно, где 
- количество нормируемых вероятностей (частот). Каждой из выявленных (обнаруженных) опасностей и исходу, не связанному с наступлением ущерба, ставят в соответствие одно из качественных значений вероятностей наступления ущерба и соответствующий весовой коэффициент.
Вероятность (частота) наступления ущерба, вызванного проявлением 
-й опасности, определяют путем деления -го весового коэффициента на сумму весовых коэффициентов, присвоенных идентифицированным опасностям и исходу, не связанному с наступлением ущерба:
. (5)
Аналогично определяют вероятность (частоту) исхода, не связанного с наступлением ущерба.
Например, качественным значениям вероятности, нормируемой по трем ступеням (низкая, средняя и высокая) путем экспертной оценки присвоены весовые коэффициенты 1, 3 и 7 соответственно. Трехуровневая шкала вероятностей (частот) и их вербальное описание представлены в таблице Б.2.
Таблица Б.2 - Пример трехуровневой шкалы вероятностей (частот)
|
|
| Вероятность | Весовой коэффициент | Вербальное описание вероятностей (частот) проявления опасностей и наступления ущерба |
| Низкая | Опасность или ее проявления, которые могут вызвать определенный ущерб, не должны возникнуть за все время профессиональной деятельности работника | |
| Средняя | Опасность или ее проявления, которые могут вызвать определенный ущерб, возникают лишь в определенные периоды профессиональной деятельности работника | |
| Высокая | Опасность или ее проявления, которые могут вызвать определенный ущерб, возникают постоянно в течение всей профессиональной деятельности работника |
Вероятности (частоты) с использованием трехуровневой шкалы определяют следующим образом. Например, идентифицированы четыре опасности. Экспертным путем установлены качественные значения вероятностей наступления ущербов: низкая, средняя, средняя и высокая. При этом вероятность исхода, не связанного с наступлением ущерба, оценивают как среднюю. Этим вероятностям соответствуют весовые коэффициенты 1, 3, 3, 7, 3 соответственно (см. таблицу Б.2). Тогда численные значения вероятностей (частот) наступления ущербов составят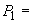 
1/17, 
3/17, 
3/17, 
7/17 и 
3/17 соответственно.