ОЦЕНКА АЛЬФА-РАЗНООБРАЗИЯ

Альфа-разнообразие — внутреннее разнообразие местооби­тания или одного сообщества.

Существует 3 возможных типа мер альфа-разнообразия, оп­ределенных Такером (2000):

• видовое богатство, определяемое как число видов, присут­ствующих на определенной территории (от небольшого место­обитания до страны или биогеографического региона);

• численность вида (обычно какой-то его популяции);

• видовое разнообразие, т. е. соотношения числа видов и их численностей.

Для количественной оценки альфа-разнообразия обычно ис­пользуют два подхода:

• построение кривых относительного обилия или доминиро­вания — разнообразия;

• расчет индексов, представляющих различные математиче­ские выражения.

При расчете индексов для оценки альфа-разнообразия прини­маются во внимание 2 фактора:

• видовое богатство — число видов, отнесенное к определен­ной площади;

• выравненность и доминирование — равномерность распре­деления видов по их обилию в сообществе.

1.1. Индексы видового богатства

Важной мерой оценки разнообразия для ограниченного в пространстве и во времени сообщества, для которого точно из­вестно число составляющих его видов и особей, является видовое богатство. Однако в большинстве случаев исследователь имеет дело с выборкой, не располагая полным списком видов сообщест­ва. В этом случае необходимо использовать нумерическое видо­вое богатство, т. е. число видов на строго оговоренное число осо­бей или на определенную биомассу, и видовую плотность.

Видовая плотность — число видов, отмечаемых на опреде­ленной, заранее оговоренной территории (например, на 1 м², 1 га). Это один из наиболее распространенных показателей видо­вого богатства. Видовое разнообразие в разных местах часто за­висит от шкалы измерения разнообразия (Мэгарран, 1992). На­пример, в 1 м² полуестественных европейских пастбищ может быть больше видов, чем в нижнем ярусе дождевого тропического леса в бассейне Амазонки. Разнообразие видов на 1 км и более будет выше в тропическом лесу. Данный показатель очень силь­но зависит от размеров изучаемой площади, поэтому при сравне­нии разновеликих территорий для частичного устранения дан­ной зависимости используют индекс концентрации видового бо­гатства D_{c r}:

 

,

 

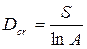где S — число видов; А — площадь местообитания.

Занимаясь изучением биологического разнообразия на ка­кой-либо территории, исследователь, как правило, не знает пол­ного числа видов живых организмов, которые там находятся. Имея дело с выборками организмов из данного местообитания, он может учесть только число видов, которые попали в эти вы­борки (S). При этом вероятность выявления каждого вида будет прямо пропорциональна его частоте встречаемости. Как прави­ло, обильные виды выявляются уже при небольшом размере вы­борок, тогда как очень редкие могут не быть обнаружены даже при больших размерах выборок. И чем больше выборка — тем выше вероятность выявления полного видового состава изучае­мого сообщества.

Довольно часто возникает необходимость сравнить между со­бой видовое богатство сообществ, по которым у исследователя имеются выборки различного объема. В этом случае следует учи­тывать, что различное число видов в выборках может быть вы­звано как различиями в видовом богатстве сообществ, так и раз­мерами выборок. Для преодоления этой проблемы был разрабо­тан так называемый метод разрежения, а также предложено большое число индексов.

Метод разрежения позволяет рассчитать число видов в так называемой редуцированной выборке (т. е. выборке меньших размеров по сравнению с исходной). Этот метод впервые был предложен Сандерсом (1968), но в дальнейшем для обеспечения несмещенной оценки он был преобразован Хэлбертом (1971). При этом можно оценить ожидаемое число видов E(S_N') в выбор­ке объемом N' особей, взятой случайным образом из более круп­ной выборки, включающей N особей, принадлежащих к S видам.

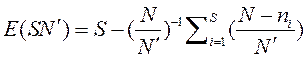
где 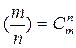— число сочетаний из т элементов по п.

Оно рассчитывается следующим образом:

 

,

 

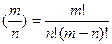где n! – n -факториал.

В основе индексов, позволяющих оценить видовое богатство, лежат различные сочетания S (число выявленных видов) и N (об­щее число особей всех S видов). Основным недостатком таких индексов является их очень сильная зависимость от объема вы­борки. В наименьшей степени этому недостатку подвержен ин­декс видового богатства Менхиника:

.

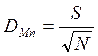Довольно широкое распространение получил также индекс, предложенный геоботаником Глизоном и гидробиологом Марга-лефом. Индекс видового богатства Глизона — Маргалефа:

.

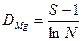Как видно из формул, данные индексы полностью зависят от объема выборки, из-за чего они не всегда пригодны, особенно при работе с группами, для которых сложно быстро и полностью выявить видовой состав. С другой стороны, для групп, в которых немного видов и они хорошо обнаруживаются, может быть быст­ро достигнута близкая к абсолютной оценка S, и вес N будет про­должать расти несмотря на логарифмирование или извлечение из корня. В то же время достоинство этих индексов — легкость расчетов. Большая величина индекса соответствует большему разнообразию.

 

1.2. Индексы видового разнообразия

Индексы видового разнообразия — это соотношения между числом видов и каким-либо показателем, имеющим значимость для сообщества и экосистемы, — численностью, биомассой, про­дуктивностью и др. (Снакин, 2000).

Цель введения различных индексов — охарактеризовать и смоделировать многокомпонентную структуру сообществ с тем, чтобы наиболее полно сравнивать их между собой (Терещенко и др., 1994). Индексы, предлагаемые для оценки биоразнообра­зия, должны отвечать определенным требованиям:

• небольшие изменения обилия массовых видов, появление и исчезновение редких видов не должны сильно влиять на величи­ну индекса;

• индекс не должен зависеть от параметров, дифференциро­ванно характеризующих разные виды, т. е. он должен относить­ся ко всем видам равноценно;

• индекс должен иметь экологическую интерпретацию и об­ладать приемлемыми статистическими свойствами, т. е. просто­той в понимании и расчетах;

• вклад отдельных видов в величину индекса должен быть пропорционален их обилию.

Среди общего числа видов, образующих сообщество, некото­рые могут преобладать по какому-то показателю (численность, биомасса, продуктивность) — их называют доминирующими. В этом случае велика вероятность того, что значительная часть оставшихся в сообществе видов будет иметь минимальные пока­затели, т. е. являться редкими. В то же время возможен и диа­метрально противоположный случай, когда доминантные виды отсутствуют и целый ряд видов обладает определенным обилием и достаточно равномерным распределением по тем же значимым признакам (численность и др.). В этом случае говорят о вырав­ненности (равномерном распределении) видов в структуре сооб­щества. Например, две биологические системы, состоящие из 100 особей, принадлежащих к 10 видам (т. е. одинаковое видо­вое богатство), могут иметь два крайних варианта распределения особей: максимальное доминирование и минимальную выравнен-ность (91 особь принадлежит к одному виду, а остальные 9 — к девяти различным видам); максимальную выравненность и отсутствие доминирования (каждый из 10 видов представлен десятком особей). На показателях доминирования или выравненности чаще всего основан расчет тех или иных индексов.

В настоящее время существует более 40 индексов, предназна­ченных для оценки биоразнообразия. Индексы, применяемые в анализе разнообразия сообществ, должны удовлетворять сле­дующим требованиям (Песенко, 1982):

1) разнообразие сообщества тем выше, чем больше в нем видов;

2) разнообразие сообщества тем выше, чем выше его выравненность.

Большинство различий между индексами, измеряющими био­разнообразие, заключается в том, какое значение они придают выравненности и видовому богатству.

Индекс Шеннона. Один из наиболее широко применяемых индексов видового разнообразия. Он основан на изучении веро­ятности наступления цепи событий, т, е. является информацион­ной мерой разнообразия, которая выражается в единицах неоп­ределенности или информации. Данный индекс впервые был предложен К. Шенноном в 1948 г., а в биологических исследова­ниях впервые применен Макартуром и Маргалефом в середине 1950-х гг.

Чаще всего используется основное выражение индекса

 

,

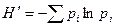где p_i – доля i-го вида в выборке. В выборке истинное значение p_i неизвестно. Оно оценивается как n_i/N, что дает смещенный ре­зультат. Это связано с тем, что расчеты индекса разнообразия Шеннона предполагают попадание в выборку особей случайно из «неопределенно большой» (т. е. практически бесконечной) гене­ральной совокупности. Более точное значение индекса можно получить из ряда

.

 

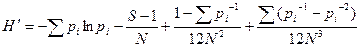Однако на практике эта ошибка редко бывает значимой. Бо­лее существенную погрешность вносит тот факт, что расчет ин­декса Шеннона предполагает наличие в выборке всех видов гене­ральной совокупности. Поэтому чем меньше видов оказалось в выборке по сравнению с их действительным количеством, тем более смещенной оказывается оценка.

При вычислении обычно используется натуральный лога­рифм, реже десятичный или логарифм по основанию 2. К сожа­лению, во многих публикациях не уточняется, какое основание применено, что затрудняет сравнение полученных данных с данными литературы, особенно когда не указано и число видов. Хотя стоит отметить, что в настоящее время прослеживается ус­тойчивая тенденция к стандартизации расчетов путем использо­вания натурального логарифма.

Индекс Шеннона обычно варьирует в пределах от 1,5 до 3,5, очень редко превышая 4,5. Как показывают расчеты, для полу­чения значения индекса Шеннона, равного 5, необходимо опери­ровать выборкой, в которой содержится 10⁵ видов.

Индекс Шеннона имеет оценку дисперсии и стандартной ошибки, что допускает основные статистические процедуры. Если рассчитать индекс Шеннона для нескольких выборок, то полученные значения будут распределены нормально. Это позво­ляет применять мощные параметрические методы анализа, вклю­чая дисперсионный, что особенно полезно в том случае, если есть повторности.

Дисперсию индекса Шеннона (VarH´) рассчитывают по фор­муле

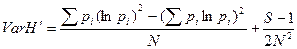
Для проверки значимости различий между выборочными со­вокупностями значений индекса Шеннона можно использовать параметрический критерий Стьюдента:

.

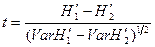Число степеней свободы определяется по уравнению:

,

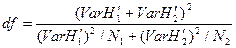где N₁ и N₂ — общее число видов в двух выборках.

Индекс выравненности по Шеннону, или индекс Пиелу. Яв­ляясь индексом разнообразия, индекс Шеннона учитывает как видовое богатство, так и выравненность видов в выборке. В то же время на основе индекса Шеннона можно получить индекс, кото­рый оценивает только выравненность. Выравненность по Шенно­ну рассчитывается исходя из того, что при одном и том же объеме выборки и числе видов максимальное значение этот индекс при­нимает при равном обилии всех входящих в выборку видов. Если же доля какого-то одного вида (в случае доминирования) стремится к 1, а всех остальных — к 0, то значение индекса также стре­мится к 0. Показатель выравненности Е рассчитывается как отно­шение наблюдаемого разнообразия к максимальному:

.

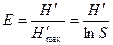Е имеет значения от 0 до 1, причем чем выше значение, тем более выровнена выборка. При этом Е = 1 соответствует равному обилию всех видов, входящих в выборку.

Индекс Шелдона.. Представляет собой экспоненциальную фор­му индекса Шеннона:

SH = ехр (Н').

Он принимает значения от 1 (наличие только одного вида) до N в случае максимально разнообразного сообщества, в котором каждый вид представлен только одной особью. С биологической точки зрения индекс Шелдона показывает, какое число видов со­держится в гипотетической выборке с равнообильными видами, разнообразие которой равно наблюдаемому (Песенко, 1982).

Индекс Бриллуэна. Когда невозможно гарантировать слу­чайный отбор объектов в выборочную совокупность или учесть все виды сообщества, более подходящей по сравнению с индек­сом Шеннона формой информационно-статистического индекса может быть индекс Бриллуэна. Он рассчитывается по формуле

.

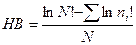Индекс Бриллуэна дает сходную с индексом Шеннона вели­чину разнообразия, редко превышая 4,5. Однако при оценке од­них и тех же данных его величина ниже индекса Шеннона. Это объясняется отсутствием в нем неопределенности, свойственной индексу Шеннона. Главным различием индексов является то, что индекс Шеннона всегда дает одну и ту же величину, если число видов и их относительные обилия остаются постоянными, а индекс Бриллуэна этим свойством не обладает.

К недостаткам индекса можно отнести относительную слож­ность расчетов, возможность получить неверные выводы при сравнении малых выборок и невозможность применения индек­са к выборкам, имеющим большую долю неопределенности. В то же время этот индекс рекомендуется использовать, если оцени­вается коллекция, а не случайная выборка, и если известен пол­ный состав сообщества.

Индекс выровненности по Бриллуэну. При его применении (аналогично индексу Шеннона) выравненность определяется как отношение наблюдаемого разнообразия к максимальному:

 

.

 

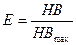Максимальное значение индекса Бриллуэна рассчитывается по формуле

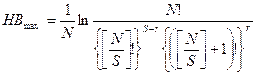
где [N/S] — целая часть отношения N/S, а r = N - S[N/S].

Индекс Симпсона. Данный индекс, иногда называемый ме­рой концентрации, описывает вероятность принадлежности лю­бых двух особей, случайно отобранных из неопределенно большо­го сообщества, к разным видам следующей формулой:

,

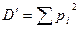где p_i — доля особей i-ro вида.

В том случае, если имеется конечное сообщество, для расчета индекса должна быть применена формула:

,

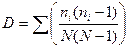где n_i — число особей i-го вида; N — общее число особей.

С точки зрения теории вероятностей приведенные выше фор­мулы имеют следующий биологический смысл. Представим, что две особи случайным образом изымаются из сообщества, имею­щего N особей, принадлежащих к S видам, из которых n_i особей принадлежат i-му виду. Тогда первая формула соответствует ве­роятности того, что обе особи принадлежат к одному виду при условии, что они будут возвращены в сообщество. Вторая форму­ла отражает то же, но с условием, что учтенные особи не будут возвращены в сообщество. Это обусловливает заниженные оцен­ки при расчетах по второй формуле по сравнению с первой, так как в этом случае игнорируются виды, представленные в сообще­стве одной особью.

Индекс Симпсона с биологической точки зрения можно ин­терпретировать еще и как меру концентрации главного ресурса в распоряжении немногих видов. Он обладает следующими свой­ствами: равен нулю при S = 0; стремится к нулю при S→ ∞, равен единице при S = 1. Он имеет оценку дисперсии и стандартной ошибки.

Вероятность межвидовых встреч. По мере увеличения зна­чения индекса Симпсона разнообразие уменьшается, поэтому в качестве меры разнообразия часто используется дополнение к данному индексу (1 - D) или (1 - D'). Эта величина носит назва­ние «вероятность межвидовых встреч» и варьирует от 0 до 1:

 

PIE'=1-D'=1- ∑ p_i²,

 

.

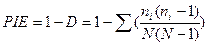Для данного индекса можно рассчитать максимальное и ми­нимальное значения разнообразия в выборке с данными N и S, соответствующие крайним типам распределения особей по видам в ней. Разнообразие выборки будет максимальным в том случае, когда все особи будут равномерно распределены по видам:

,

,

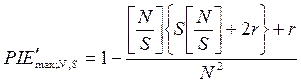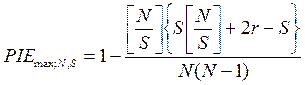где [N/S] — целая часть отношения N/S;r — остаток от деления N на S, целое число меньше S; r = N - S[N/S].

Минимальные оценки PIE' и PIE, соответствующие крайне неравномерному распределению N особей по S видам, вычисля­ются по следующим формулам:

,

.

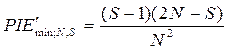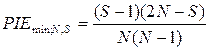Исходя из полученного реального значения индекса вероят­ности межвидовых встреч для изучаемой выборки, а также из рассчитанных минимального и максимального значений для вы­борки с такими же значениями N и S, можно оценить ее выравненность.

Индекс полидоминантности. В качестве меры разнообра­зия, рассчитанной на основании индекса Симпсона, может быть использовано отношение данного индекса к единице, которое иногда называют индексом полидоминантности. Он показывает, какое число видов присутствует в гипотетической выборке, где все виды равнообильны, если она имеет такое же разнообразие, как данная выборка (Песенко, 1982). Рассчитывается индекс полидоминантности по следующим формулам:

,

.

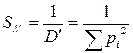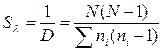Индексы полидоминантности служат полезными трансфор­мациями PIE' и PIE в том случае, когда анализируемые выбор­ки имеют высокие значения индекса вероятности межвидовых встреч или если желательно выразить разнообразие в таких ин­терпретируемых единицах, как число видов.

Индексы Макинтоша. В том случае, если выборка состоит из N особей, распределенных по S видам, и численность i-гo вида равняется n_i, эту выборку можно представить в S-мерном гипер­пространстве как точку с координатами (n₁, п₂,..., n_s). В 1967 г. Макинтош предложил в качестве индекса, измеряющего разно­образие, евклидово расстояние от точки, соответствующей вы­борке, до точки начала координат (0, 0,..., 0):

.

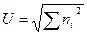Из формулы видно, что при одном и том же числе особей чем большее число видов включает выборка, тем меньше U. Следова­тельно, индекс Макинтоша U сам по себе не является индексом доминирования, а измеряет, наоборот, однообразие выборки. Поэтому в качестве меры разнообразия может быть использова­но N-дополнение до U:

 

.

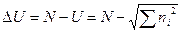Эти индексы очень редко непосредственно используются при анализе биоразнообразия, так как являются ненормированными и очень чувствительными к размеру выборки. В то же время, используя их, можно рассчитать индекс разнообразия D, который независим от объема выборки:

.

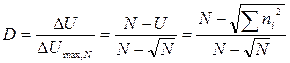Данный индекс имеет диапазон значений от нуля при нали­чии в выборке только одного вида до единицы в том случае, если в выборке каждый вид представлен только одной особью. Мини­мум этого индекса для выборки с N особями S видов достигается при ее крайней невыравненности:

,

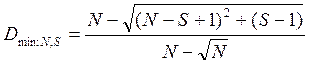а максимум — при полной выравненности:

.

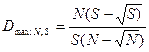Исходя из полученных значений, можно рассчитать выравненность выборки:

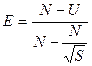
Индекс Бергера — Паркера. Этот индекс является одним из наиболее простых и легко интерпретируемых индексов домини­рования. Его достоинство — простота вычисления. Индекс Бер­гера — Паркера представляет собой долю самого массового вида в выборке:

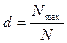
где N_max —число особей самого обильного вида.

Так как при увеличении степени доминирования одного вида и, как следствие этого, увеличении величины индекса Бергера — Паркера происходит уменьшение разнообразия, то обычно ис­пользуется величина, обратная индексу Бергера — Паркера, 1/d. При этом увеличение индекса 1/d соответствует увеличению раз­нообразия и снижению степени доминирования одного вида. Этот индекс независим от количества видов, но на него влияет объем выборки.

 

1.3. Модели распределения видового обилия

Анализ распределения обилий видов является самым полным математическим описанием всей собранной по сообществу ин­формации (Мэгарран, 1992). Имеющиеся реальные данные по видовому обилию того или иного сообщества можно описать од­ним или несколькими распределениями. На сегодняшний день известно большое количество математических моделей, с помо­щью которых можно описать видовое обилие тех или иных сооб­ществ, но все же разнообразие чаще всего анализируется с уче­том четырех основных теоретических моделей: геометрического, логарифмического (лог-ряда), логарифмически-нормального (лог-нормального) распределения и распределения, описываемого мо­делью «разломанного стержня» Макартура.

Каждую из моделей можно представить в виде графиков, на которых по оси абсцисс будет указан порядковый номер видов от наиболее обильных до самых немногочисленных, а по оси орди­нат — их обилие в логарифмической шкале (рис. 1). При этом можно увидеть переход от геометрического ряда к модели «раз­ломанного стержня». В случае геометрического распределения доминируют немногие виды при очень низкой численности боль­шинства, при логарифмическом и лог-нормальном распределении виды со средним обилием становятся все более и более обычны­ми; в распределении, описывае­мом моделью «разломанного стерж­ня», обилия видов распределены с максимально возможной в при­роде равномерностью.

 

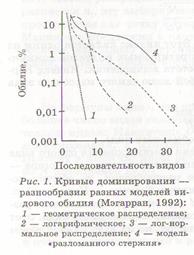Каждой из моделей соответст­вует характерная кривая на гра­фике ранг/обилие (рис. 1). Гео­метрическое распределение выра­жается прямой линией с крутым наклоном. Логарифмическое рас­пределение также имеет крутой наклон, но это не прямая линия, а кривая. Модель «разломанного стержня» имеет более пологий график. Лог-нормальное распределение

 

 

описывается S-образной кривой, которая располагается на графике между логарифмическим распределением и моделью «разломанного стержня».

Геометрический ряд. Данное распределение описывает ситуа­цию, при которой наиболее обильный вид захватывает часть k некоего ограниченного ресурса, второй по обилию вид захваты­вает такую же долю k остатка этого ресурса, третий по обилию — k от остатка и т. д., пока ресурс не будет разделен между всеми S видами. Если это условие выполнено и если обилия видов (выра­женные, например, их биомассой, проективным покрытием или числом особей) пропорциональны используемой доле ресурса, распределение этих обилий будет описываться геометрическим рядом (или гипотезой преимущественного захвата ниши).

Модель имеет два параметра: n_i — численность самого обиль­ного вида и k — константу геометрической прогрессии. При этом обилия видов от наибольшего к наименьшему можно рассчитать с помощью формулы

 

,

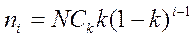где n_i — число особей i-ro вида; N — общее число особей;

С_к = [l - (1 - k)^s]^-1 — константа, при которой ∑ n_i = N.

Распределение обилий видов по типу геометрического ряда обнаруживается преимущественно в бедных видами местообита­ниях или в сообществах на очень ранних стадиях сукцессии. Та­кое распределение характерно для некоторых растительных со­обществ в суровых условиях окружающей среды (например, со­общество растений субальпийского пояса).

Логарифмический ряд (лог-ряд). Данное распределение, так же как и геометрический ряд, описывает ситуацию заселения биотически ненасыщенного местообитания, но в отличие от него виды проникают в сообщество не через равные, а через случай­ные промежутки времени. Распределение частот видов для лог-ряда описывается формулой:

,

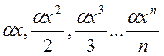где 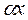— число видов, представленных одной особью; 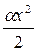- число

видов, представленных двумя особями и т. д.

Общее число видов S рассчитывается в результате сложения всех членов данного ряда, что в конечном итоге приводит к ра­венству:

S = S₁+S₂+...= -α ln(l-x).

Входящая в это уравнение константа х оценивается путем итерационного решения уравнения:

,

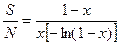где N — общее число особей.

На практике х почти всегда больше 0,9 и никогда не превы­шает 1,0. Если N/S > 20, х > 0,99.

α — это индекс лог-ряда, который можно получить из урав­нения:

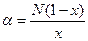
с доверительными пределами, устанавливаемыми выражением

.

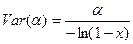Довольно широко α используется как индекс видового разно­образия, причем он может применяться даже в том случае, если распределение обилий видов в изучаемом сообществе не подчи­няется логарифмическому распределению.

Для того чтобы оценить соответствие распределения обилий особей в конкретном местообитании лог-ряду, необходимо рас­считать число видов, ожидаемое в каждом классе обилия, и срав­нить его с действительно наблюдаемым. Для сравнения и оценки достоверности различий используются критерии согласия (чаще всего χ²).

Моделью логарифмического распределения, характеризующей­ся малым числом обильных видов и большой долей редких, с наи­большей вероятностью можно описать такие сообщества, структу­ра которых определяется одним или немногими экологическими факторами. Так, к примеру, такому ряду соответствует распреде­ление обилий видов растений наземного яруса в хвойных культу­рах в условиях низкой освещенности (Мэгарран, 1992).

Логарифмически нормальное распределение. Данный тип распределения характерен для систем, когда величина некоей переменной определяется большим числом факторов. Например, лог-нормальное распределение обилий видов характерно для больших, зрелых и разнообразных сообществ.

Эта модель впервые была применена к распределению обилий видов Престоном (Preston, 1948). При построении графика он на­нес обилия видов на ось в log₂-шкале и назвал получившиеся классы октавами. В случае использования логарифма по основа­нию 2 каждая октава будет соответствовать удвоенному обилию предыдущей, но для описания модели можно использовать лю­бое основание логарифма. На графике распределения частот ви­дов по полученным таким способом классам численности соот­ветствуют известной кривой нормального распределения, усе­ченной слева, в области частот редких видов. Распределение обычно записывается в форме:

,

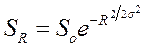где S_R — теоретическое число видов в октаве, расположенной в R октавах от модальной октавы; S₀ — число видов в модальной ок­таве; σ — стандартное отклонение теоретической лог-нормальной кривой, выраженное в числе октав.

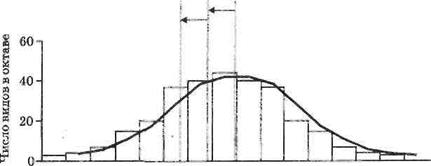
Лог-нормальное распределение описывается симметричной «нормальной», т. е. колоколообразной, кривой (рис. 2.). Однако чем меньше объем выборки, на основании анализа которой стро­ится распределение, тем больше вероятность того, что очень ред­кие виды, представленные небольшим числом особей, в нее не попадут. На графике это выражается в том, что левая часть кривой будет выражена нечетко, располагаясь за так называемой «линией занавеса». «Линия занавеса» сдвигается влево при уве­личении объема выборки, хотя, как правило, при анализе не­больших сообществ бывает выражена только часть кривой справа от моды. Только при огромном количестве данных, собранных на, обширных биогеографических территориях, прослеживается полная кривая (Мэгарран, 1992).

-7-6-5-4-3-2-10 1 2 3 4 5 6 7

Октавы

Рис. 2. Лог-нормальное распределение. Стрелками обозначен сдвиг «линии занавеса» при увеличении объема выборки

 

Распределение по модели «разломанного стержня» Макартура. Эту модель иногда называют гипотезой случайной границы ниши. S видов разделяют среду случайно между собой так, что занимают неперекрывающиеся ниши. При этом число особей ка­ждого вида пропорционально размеру (ширине) ниши. Такое разделение пространства ниши в пределах сообщества можно об­разно сравнить со случайным и одновременным разламыванием стержня на S кусков.

Эта модель рассматривает только один ресурс. Она отражает более равномерное его разделение, чем лог-нормальная модель, логарифмическая и геометрическая модели. Модель «разломан­ного стержня» характеризуется только одним параметром S (чис­лом видов) и сильно зависит от объема выборки.

Число особей в i-м классе по порядку обилия среди S видов (N_i) получают по формуле

,

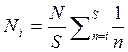где N - общее число особей; S — общее число видов.

Эту модель можно выразить также в величинах стандартного распределения обилий видов:

,

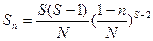где S(n) — число видов в классе обилия с п особями.

Как и в рассмотренных выше случаях лог-ряда и лог-нор­мального распределения, для сравнения ожидаемых и наблюда­емых частот классов обилия используют критерии согласия.

Модель Макартура предполагает, что пространство ниш поде­лено на случайные, соприкасающиеся, но неперекрывающиеся участки. Такое распределение характерно для сообществ с ин­тенсивной межвидовой конкуренцией, территориальным поведе­нием. Лучше всего использовать модель «разломанного стерж­ня» для доказательства большей выравненности обилий видов в определенном сообществе.