Для каждого колебания (пружина, маятник, контур) вы должны хорошо знать частоту колебаний и уметь писать закон сохранения энергии. Если нужен период, находите его по выведенной выше формуле T=2π/ω.
При гармонических колебаниях x = xмакс.cos(ωt) или x = xмакс.sin(ωt). Берем косинус, если начальное значение x (то есть x при t=0) равно максимальному, берем синус – если оно равно нулю. Например, растянули пружину и отпустили, x в начальный момент максимальное, поэтому берем косинус. Но если в начальный момент x=0 (грузик находится в положении равновесия), то берем синус. Если в начальный момент конденсатор заряжен (и затем разряжается в контуре), то пишем Q = Qмакс.cos(ωt), если конденсатор разряжен в начальный момент, пишем Q = Qмакс.sin(ωt).
Если тело совершает колебания по закону x=10cos(16πt), то амплитуда равна 10,
ω равна 16π, ν равно ω/2π=8, период колебаний равен 1/8 сек.
Если груз колеблется от 0 до 20 см, то его амплитуда равна 10 см.
Если в задаче даны максимальные значения, сразу пишите закон сохранения энергии.
При колебаниях ток не постоянен, поэтому можно использовать определение тока только как производной от заряда по времени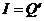 
. Если вам дано, что Q = Qмакс.cos(ωt), и надо найти ток, то берете производную I=Q'=ωQмакс.cos(ωt). Iмакс.= ωQмакс. Для контура эту формулу можно получить и через закон сохранения энергии.
Если забыли, что на что надо делить, чтобы получить частоту, то проверяйте через размерность. Например, если сомневаетесь, ω равна корень из g/l или l/g, то подставляете размерность g – м/сек2 и размерность l – м. Получаете, что корень из g/l имеет размерность 1/сек, значит, это частота, а корень из l/g имеет размерность сек, значит, это период (точнее T=2π√l/g).
Гребень волны – это точка максимума, то есть точка, где косинус=1. Значит, фаза (то, что под косинусом) в гребнях равны 0; 2π; 4π и так далее. Получается, что фаза у гребней отличается на 2π. Так как расстояние между гребнями есть длина волны, то при перемещении на длину волны фаза сдвигается на 2π. Соответственно, при перемещении на полволны фаза сдвигается на π, и т.д.
Колебания грузика на пружине на прямой по закону x = xмакс.cos(ωt) можно представить так, как будто грузик двигается по кругу радиуса xмакс с постоянной скоростью, и его положение на прямой (то есть x) есть проекция его положения на круге на ось X. Таким образом мы движение по прямой с переменной скоростью заменяем на движение по кругу с постоянной скоростью. Полное колебание представляем как один оборот. Изменение фазы на φ представляем как поворот на угол φ, угол поворота φ и фаза становятся одним и тем же.
Теория относительности.
Лекция: "Теория оносительности".
Определения.
В теории относительности многие величины определяются и вычисляются по-другому (например: время, длина, импульс, кинетическая энергия, масса), но это не входит в школьную программу.
Законы.
Постулаты теории относительности
- Любые физические явления протекают одинаково в любых инерциальных системах отсчета (ИСО).
- Скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника и наблюдателя.
Выводится:
В движущейся ИСО время замедляется, длина становится меньше.
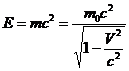
У фотона нет массы покоя, его импульс считается так: 