Неоднородное уравнение теплопроводности
Пусть внутри стержня имеются источники или поглотители тепла с известной плотностью распределения их. В этом случае процесс распространения тепла описывается неоднородным уравнением (1.183). Определим закон изменения температуры в стержне для граничных условий первого рода.
А Однородная краевая задача
Рассмотрим неоднородное уравнение

с нулевыми (однородными) граничными условиями
 , ,  , ,
| (1.214) |
и начальным условием
 . .
| (1.215) |
Будем искать решение этой задачи в виде
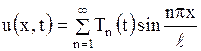 . .
| (1.216) |
Тогда граничные условия удовлетворяются автоматически.
Предположим, что функция  , рассматриваемая как функция от
, рассматриваемая как функция от  при фиксированном
при фиксированном  , может быть разложена в ряд Фурье
, может быть разложена в ряд Фурье
 , ,
| (1.217) |
где
 . .
| (1.218) |
Подставляя в уравнение (1.183) ряд (1.216) (предполагаемое решение) и принимая во внимание (1.217), будем иметь
 ,
,
откуда получим
 , где , где  . .
| (1.219) |
Пользуясь начальным условием (1.214)
 ,
,
получаем начальное условие для 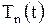 :
:
 . .
| (1.220) |
Найдем решение обыкновенного дифференциального уравнения (1.219), удовлетворяющее условию (1.220), воспользовавшись методом вариации. Решение соответствующего однородного уравнения имеет вид (1.211)
 .
.
Подставив в (1.219) выражения 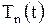 и
и  , получим дифференциальное уравнение относительно
, получим дифференциальное уравнение относительно  :
:
 ,
,
откуда находим
 .
.
Следовательно, 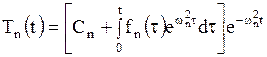
и в силу (1.220)
 .
.
Итак,
 . .
| (1.221) |
Подставляя в ряд (1.216) выражение (1.221), получим решение однородной краевой задачи (1.183), (1.214) – (1.215) в виде
 . .
| (1.222) |
Если начальное условие неоднородно  , то к решению (1.222) нужно прибавить решение однородного уравнения теплопроводности с заданным начальным условием
, то к решению (1.222) нужно прибавить решение однородного уравнения теплопроводности с заданным начальным условием  и граничными условиями (1.214), которое получено в п.1.33.1А.
и граничными условиями (1.214), которое получено в п.1.33.1А.
Б Общая первая краевая задача
Наконец рассмотрим общую первую краевую задачу для неоднородного уравнения теплопроводности, т.е. тот случай, когда начальное и граничные условия неоднородные:
найти решение уравнения (1.183)

при граничных условиях
 , ,  , ,
| (1.223) |
и начальном условии
 . .
| (1.224) |
Задача сводится к задачам, рассмотренным в пп. 1.33.1Б, 1.33.2А. А именно, вводится функция вида
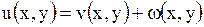 , ,
| (1.225) |
где функция  удовлетворяет однородному уравнению
удовлетворяет однородному уравнению
 , ,
| (1.226) |
граничным условиям
 , , 
| (1.227) |
и начальному условию
 , ,
| (1.228) |
а функция  удовлетворяет неоднородному уравнению
удовлетворяет неоднородному уравнению
 , ,
| (1.229) |
граничным условиям
 , , 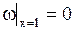
| (1.230) |
и начальному условию
 . .
| (1.231) |
Легко доказать, что сумма (1.225) является решением общей краевой задачи.
Распространение тепла в бесконечном стержне.
Решение задачи Коши для однородного уравнения
теплопроводности методом интеграла Фурье
Рассмотрим задачу о распределении температуры в однородном неограниченном стержне, теплоизолированном по всей длине, при известном начальном (при  ) распределении температуры.
) распределении температуры.
Математическая постановка задачи: найти функцию  , ограниченную в области
, ограниченную в области  ,
,  , удовлетворяющую уравнению
, удовлетворяющую уравнению
  , , 
| (1.232) |
и начальному условию
 , ,  . .
| (1.233) |
Сформулированная задача есть задача Коши.
Применим метод разделения переменных и суперпозиции частных решений.
Ищем частные решения уравнения (1.232) в виде произведения двух функций одной переменной
 . .
| (1.234) |
Подставляя (1.234) в (1.232) и разделяя переменные, получим
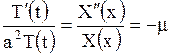 ,
,  .
.
Откуда следует
 , ,
| (1.235) |
 . .
| (1.236) |
Из уравнения (1.235) находим
 . .
| (1.237) |
Функции  и
и  должны быть ограниченными, т.к. температура
должны быть ограниченными, т.к. температура  не может неограниченно возрастать в результате свободного теплообмена. Из (1.236) видно, что параметр разделения
не может неограниченно возрастать в результате свободного теплообмена. Из (1.236) видно, что параметр разделения  не может быть отрицательным; если
не может быть отрицательным; если 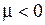 , то
, то  при
при  , а это не имеет физического смысла. Следовательно,
, а это не имеет физического смысла. Следовательно,  . Обозначим для удобства последующих выкладок
. Обозначим для удобства последующих выкладок  . В выражении (1.237) положим
. В выражении (1.237) положим  . Тогда
. Тогда
 .
.
Как известно, для линейного уравнения (1.236) общее решение имеет вид
 .
.
Так как граничные условия отсутствуют, то параметр  остается совершенно произвольным. Произвольные постоянные
остается совершенно произвольным. Произвольные постоянные 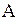 и
и  для каждого
для каждого  имеют определенные значения. Поэтому
имеют определенные значения. Поэтому 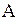 и
и  можно считать функциями от
можно считать функциями от  . Согласно (1.234) каждому значению
. Согласно (1.234) каждому значению  соответствует частное решение
соответствует частное решение
 . .
| (1.238) |
В случае стержня конечной длины  мы определили из граничных условий дискретное множество возможных значений параметра
мы определили из граничных условий дискретное множество возможных значений параметра  :
: 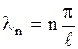 , где каждому
, где каждому 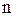 соответствуют некоторые коэффициенты
соответствуют некоторые коэффициенты  и
и  . Чем длиннее стержень, тем гуще множество значений
. Чем длиннее стержень, тем гуще множество значений  (расстояние между
(расстояние между  и
и  равно
равно  и стремится к нулю, когда
и стремится к нулю, когда  ). Поэтому для бесконечного стержня
). Поэтому для бесконечного стержня  может иметь любое значение от 0 до
может иметь любое значение от 0 до  . Таким образом, первая часть метода – построение частных решений – завершена.
. Таким образом, первая часть метода – построение частных решений – завершена.
Вторая часть метода Фурье – суперпозиция частных решений 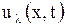 ,
,  . Уравнение (1.232) линейное и однородное; оно имеет, как мы только что установили, бесчисленное множество частных решений, зависящих от непрерывно меняющегося параметра
. Уравнение (1.232) линейное и однородное; оно имеет, как мы только что установили, бесчисленное множество частных решений, зависящих от непрерывно меняющегося параметра  . Поэтому общее решение получается из частных (1.238) не суммированием по счетному множеству значений
. Поэтому общее решение получается из частных (1.238) не суммированием по счетному множеству значений  , а интегрированием по параметру
, а интегрированием по параметру  :
:
 . .
| (1.239) |
Для того чтобы убедиться, что функция (1.239) действительно является решением уравнения (1.232), надо продифференцировать (1.239) по  и по
и по  и результаты дифференцирования подставить в уравнение. Не проводя эту операцию, которая требует определенных знаний об интегралах по параметру, будем исходить из доказанного в литературе утверждения: интеграл (1.239) является решением уравнения (1.232) при любых абсолютно интегрируемых функциях
и результаты дифференцирования подставить в уравнение. Не проводя эту операцию, которая требует определенных знаний об интегралах по параметру, будем исходить из доказанного в литературе утверждения: интеграл (1.239) является решением уравнения (1.232) при любых абсолютно интегрируемых функциях  и
и  . Подберем функции
. Подберем функции  и
и  так, чтобы решение (1.239) удовлетворяло начальному условию (1.233). Полагая в (1.239)
так, чтобы решение (1.239) удовлетворяло начальному условию (1.233). Полагая в (1.239)  , получим в силу (1.233)
, получим в силу (1.233)
 . .
| (1.240) |
Интеграл, стоящий справа, есть интеграл Фурье (одна из его форм), который является обобщением понятия ряда Фурье.
В теории интеграла Фурье доказывается, что любая непрерывная функция  , абсолютно интегрируемая, т.е. удовлетворяющая условию
, абсолютно интегрируемая, т.е. удовлетворяющая условию
 ,
,
может быть представлена в виде интеграла от гармонических функций  и
и  , частоты которых
, частоты которых  приобретают непрерывную совокупность значений:
приобретают непрерывную совокупность значений:
 , ,
| (1.241) |
где
 , ,  . .
| (1.242) |
В равенстве (1.241) нетрудно усмотреть сходство с рядом Фурье для функции  , а в выражениях (1.242) – сходство с коэффициентами Фурье.
, а в выражениях (1.242) – сходство с коэффициентами Фурье.
Сравнивая равенства (1.240) и (1.241), получаем выражения
 , , 
| (1.243) |
в предположении, что заданная функция  непрерывна и абсолютно интегрируема.
непрерывна и абсолютно интегрируема.
Найдя таким образом коэффициенты  и
и  по формулам (1.243) и подставив их в интеграл (1.240), получим
по формулам (1.243) и подставив их в интеграл (1.240), получим
 Внесем
Внесем  и
и  под знак внутренних интегралов, тогда
под знак внутренних интегралов, тогда

Учитывая, что выражение в круглых скобках есть косинус разности, приходим к следующему представлению:
 .
.
Последний интеграл можно еще преобразовать, изменив порядок интегрирования:
 . .
| (1.244) |
По существу задача решена. Построенная функция  есть решение данного уравнения, удовлетворяющее заданному начальному условию. Можно только преобразовать полученное выражение к более удобному виду, который позволит придать физический смысл решению задачи теплопроводности в бесконечном стержне.
есть решение данного уравнения, удовлетворяющее заданному начальному условию. Можно только преобразовать полученное выражение к более удобному виду, который позволит придать физический смысл решению задачи теплопроводности в бесконечном стержне.
Займемся вычислением внутреннего интеграла; положим в нем  ,
,  , откуда найдем
, откуда найдем  ,
,  . В результате имеем
. В результате имеем
 .
.
Последний интеграл может быть вычислен следующим специальным приемом. Обозначим
 . .
| (1.245) |
Дифференцируя интеграл  по параметру
по параметру 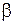 , найдем, что
, найдем, что
 .
.
Преобразуем 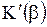 , проинтегрировав по частям:
, проинтегрировав по частям:

Таким образом, имеем дифференциальное уравнение

Интегрируя его, получим
 .
.
Откуда находим
 .
.
Определим  . Из (1.245) имеем
. Из (1.245) имеем  - интеграл Пуассона. Как известно,
- интеграл Пуассона. Как известно,  . В силу этого
. В силу этого

и
 .
.
Подставляя это выражение интеграла в решение (1.244), найдем

и окончательно
 . .
| (1.246) |
Заметим, что полученный интеграл (1.246), называемый интегралом Пуассона, довольно труден для вычисления: он не берется в элементарных функциях. Однако задача считается решенной, если удается выразить этот интеграл через табулированную функцию  , известную в теории вероятностей под названием интеграла ошибок.
, известную в теории вероятностей под названием интеграла ошибок.
Функцию
 , ,
| (1.247) |
зависящую от  и произвольного параметра
и произвольного параметра  , часто называют фундаментальным решением уравнения теплопроводности. Функция
, часто называют фундаментальным решением уравнения теплопроводности. Функция  удовлетворяет уравнению теплопроводности и начальному условию, в чем нетрудно убедиться. Она имеет определенный физический смысл.
удовлетворяет уравнению теплопроводности и начальному условию, в чем нетрудно убедиться. Она имеет определенный физический смысл.
Пусть начальное распределение температуры в стержне задано функцией  , равной нулю всюду, кроме окрестности точки
, равной нулю всюду, кроме окрестности точки  , где
, где  , т.е.
, т.е.



(см. рис. 1.11). Это так называемый физический тепловой импульс. Такое начальное распределение можно истолковать следующим образом: до момента  весь стержень находился при нулевой температуре и в момент
весь стержень находился при нулевой температуре и в момент  малому интервалу
малому интервалу  , т.е. элементу длины
, т.е. элементу длины  стержня, сообщили некоторое количество тепла
стержня, сообщили некоторое количество тепла  (здесь
(здесь 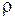 - плотность материала стержня,
- плотность материала стержня,  - его теплоемкость,
- его теплоемкость,  - масса выделенного участка), которое вызвало мгновенное повышение температуры на этом участке на величину
- масса выделенного участка), которое вызвало мгновенное повышение температуры на этом участке на величину  . Практически температура, конечно, не может представляться разрывной функцией
. Практически температура, конечно, не может представляться разрывной функцией  , но график температуры (он будет иметь примерно вид пунктирной линии) тем меньше отличается от графика
, но график температуры (он будет иметь примерно вид пунктирной линии) тем меньше отличается от графика  , чем резче и кратковременнее будет подогрев.
, чем резче и кратковременнее будет подогрев.
При таком тепловом импульсе решение (1.247) задачи теплопроводности будет иметь вид
 . .
| (1.248) |
 Будем теперь уменьшать длину интервала, на которой было подано тепло
Будем теперь уменьшать длину интервала, на которой было подано тепло  . Устремляя
. Устремляя  к нулю, т.е. переходя к мгновенному точечному источнику тепла, находящемуся в момент
к нулю, т.е. переходя к мгновенному точечному источнику тепла, находящемуся в момент  в точке
в точке  , получим из интеграла (1.248), используя теорему о среднем,
, получим из интеграла (1.248), используя теорему о среднем,
 . .
| (1.249) |
В частности, если количество тепла 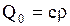 , то решение (1.249) превратится в функцию
, то решение (1.249) превратится в функцию
 ,
,
т.е. в фундаментальное решение (1.247) при значении параметра  .
.
Следовательно, точечный источник тепла с количеством тепла 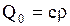 , действовавший в точке
, действовавший в точке  в момент
в момент 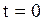 , передаст в точку
, передаст в точку  к моменту
к моменту  такое количество тепла, что температура в этой точке становится равной фундаментальному решению
такое количество тепла, что температура в этой точке становится равной фундаментальному решению  уравнения теплопроводности.
уравнения теплопроводности.
Применим теперь физический смысл фундаментального решения к физическому толкованию решения (1.246). Для того чтобы придать сечению 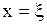 стержня температуру
стержня температуру  в начальный момент, надо распределить на малом элементе
в начальный момент, надо распределить на малом элементе  около этой точки количество тепла
около этой точки количество тепла  или, что то же самое, поместить в точке
или, что то же самое, поместить в точке  мгновенный точечный источник тепла мощности
мгновенный точечный источник тепла мощности  . Тогда, согласно (1.249), распределение температуры, вызываемое этим тепловым импульсом, будет таково:
. Тогда, согласно (1.249), распределение температуры, вызываемое этим тепловым импульсом, будет таково:
 .
.
Общее же воздействие, обусловленное начальной температурой  во всех точках стержня, может быть получено суммированием тех воздействий, которые произошли от отдельных элементов, т.е. от каждого импульса в отдельности, что и даст полученное выше решение
во всех точках стержня, может быть получено суммированием тех воздействий, которые произошли от отдельных элементов, т.е. от каждого импульса в отдельности, что и даст полученное выше решение
 .
.
Другими словами, решение (1.246) есть результат суперпозиции (наложения) температур, возникающих в точке  в момент времени
в момент времени  вследствие воздействия непрерывно распределенных по стержню тепловых импульсов «интенсивности»
вследствие воздействия непрерывно распределенных по стержню тепловых импульсов «интенсивности»  в точке
в точке  , приложенных в момент
, приложенных в момент  .
.
Формула Пуассона (1.246) обобщается в задачу Коши для уравнения теплопроводности с двумя и тремя пространственными координатами. Так, в случае распространения тепла в неограниченном пространстве уравнение теплопроводности

при начальном условии

имеет решение
 .
.