Даже прочные балки могут оказаться непригодными к эксплуатации. Если под нагрузкой они будут сильно прогибаться вследствие недостатка жёсткости.
Для обеспечения нормальной эксплуатации строительных конструкций расчёт изгибаемых балок должен производиться не только по первому состаянию(на прочность и устойчивость, но и по второму(на жёсткость)).
Второе предельное состояние конструкции харак-ся появлением чрезмерной деформацией(прогибов) и требует определение жёсткости, чтобы в условиях нормальной эксплуатации величина относительного прогиба не превышала предельно допустимого относительного прогиба установленного СНИП для различных конструкций.
f/L≤f пред/L
f- наибольшая абсолютная величина прогиба
L- пролёт или длина балки
Это условие позволяет проверять жёсткость существующей конструкции или подбирать по жёсткости сечение проектируемой конструкции.
При подборе сечения одновременно по прочности и жёсткости окончательно принимают наибольшие требуемые размеры поперечного сечения или большой номер сечения.
№42
В строительной практике элем-ты конструкций при работе могут испытывать 2 и более деформаций.
Значитони нах-ся в состоянии сложного сопротивления, например колонны, нагруженные внеЦентренно, испытывают сжатие(растяжение) и изгиб;
Валы машин- деформация кручения и т.д.
Одна из видов сложных деформ. Явл-ся КОСОЙ ИЗГИБ.
Силовая плоскость не совпадает ни с одной из условных плоскостей бруса.
На косой изгиб работают обрешётены кровли, консоли. Нагруженные сосредоточенной силой пар под углом и т.д.
Для определения нормального напряжения при косом изгибе разложим силу Fна 2 составляющие по правилу параллелограмма в результате будем иметь 2 прямых изгиба.
№43
При действии силы вне центра наблюдаем следующие деформации: сжатие и изгиб.
При сжатии:
δ= - 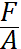
при изгибе:
δ= 
Ядром сечения наз-ся область плоского сечения, при приложение в которой продольной силы получаем во всех точках поперечного сечения напряжение одного знака.
Ядро сечения имеет большое практическое значение. Для каменных, бетонных и др. конструкций появление, растягивающих напряжений в сечений не желательно, т.к. материал плохо растягивается, поэтому силу надо приложить, чтобы не выходила за 1/3 размера сечения.
№44
Короткие массивные стержни рассчитываются только на сжатие.
Длинные стержни небольшого поперечного сечения под действием сжимающих сил- изгибаются и теряют равновесие.
Различают три вида устойчивого равновесия:
1. Устойчивое- если тело возвращается к первоначальной форме равновесия.
2. Неустойчивое – когда остаётся таким(деформированным)
3. Переходное- (или критическое состояние), т.е. может перейти и может не перейти.
Продольным изгибом назыв-ся деформация стержня в искривлении его под действием сил, направленным вдоль оси.
Критическая сила – наибольшее значение сжимающей силы, при которой прямолинейная форма стержня сохраняет устойчивость.
Критическая сила определяется по формуле Эйлера:
Где E – модуль Юнга(табл.)
Imin – осевой момент инерции
L- длина колонны
µ- коэф. Приведения длины он зависит от способа закрепления стержня.
№45
Критическое напряжение- напряжение, вызываемое критической силой
Imin – радиус инерции(минимальной) значение берём в сортаменте для проката; для простых геометрич.фигур считаем по формуле:
Imin = 
Формулой Эйлера можно пользоваться, если напряжении меньше либо равно пределу пропорциональности.
№46
При практических расчётах на устойчивость сжатых стержней вместо двух формул Эйлера и Ясинского пользуются практической формулой:
f- коэф. продольного изгиба,в табл.,в зависимости от материала и гибкости.
Отсюда три типа задач расчёта на устойчивость:
1. Проверка на устойчивость
2. Подбор сечения
3. Определение мах нагрузки