Ч. 1. Механика. Молекулярная физика, термодинамика.
Основные формулы по разделам курса физики
Механика
Поступательное движение.
Средняя (путевая) скорость:
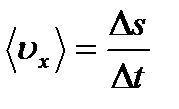 ,
,
где 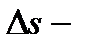 путь, пройденный точкой за интервал времени
путь, пройденный точкой за интервал времени 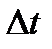 . Путь
. Путь 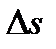 не может убывать и принимать отрицательные значения, т.е.
не может убывать и принимать отрицательные значения, т.е.  .
.
Мгновенная скорость (проекция на ось  ):
):


Среднее ускорение:
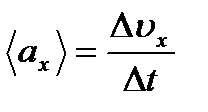
Мгновенное (линейное) ускорение (проекция на ось  ):
):
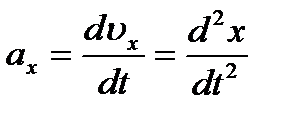 .
.
Основные уравнения кинематики поступательного движения: скорость и путь равнопеременного поступательного движения:
 ,
,
 ,
,  .
.
где 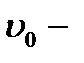 начальная скорость (в момент времени
начальная скорость (в момент времени  ); для равнозамедленного движения
); для равнозамедленного движения  , для равноускоренного
, для равноускоренного 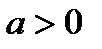 ).
).
При движении тела по вертикальному направлению в поле силы тяжести Земли 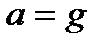 .
.
Движение материальной точки по окружности.
Угловая скорость:
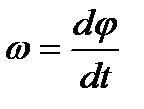 .
.
Угловое ускорение:
 .
.
Связь между линейными и угловыми величинами при движении точки по окружности:
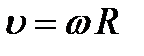 ,
, 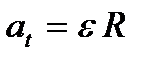 ,
, 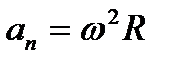 ,
,
где  модуль линейной скорости;
модуль линейной скорости;  и
и 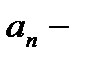 модули тангенциального и нормального ускорений;
модули тангенциального и нормального ускорений; 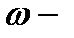 модуль угловой скорости;
модуль угловой скорости;  модуль углового ускорения;
модуль углового ускорения;  радиус окружности.
радиус окружности.
Модуль полного ускорения:
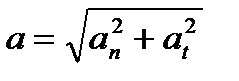 .
.
Основные уравнения кинематики вращательного движения: угловая скорость и угловой путь
 ,
,
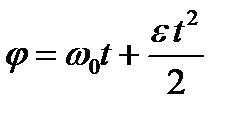 ,
, 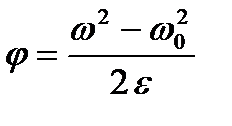 .
.
Для равнопеременного вращательного движения  ,
, 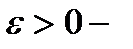 ускоренное вращение,
ускоренное вращение,  замедленное вращение.
замедленное вращение.
Связь частоты вращения n и угловой скорости:
 .
.
Связь углового перемещения и числа оборотов N:
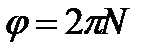 .
.
Динамика поступательного движения.
Импульс абсолютно твердого тела массой  , движущегося со скоростью
, движущегося со скоростью  :
:
 .
.
Второй закон динамики (Ньютона):
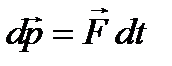 ,
,
где 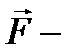 результирующая сила, действующая на материальную точку.
результирующая сила, действующая на материальную точку.
Силы, рассматриваемые в механике:
а) сила упругости  ;
;
где 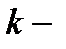 коэффициент упругости (в случае пружины – жесткость);
коэффициент упругости (в случае пружины – жесткость);  абсолютная деформация;
абсолютная деформация;
б) сила тяжести:  ;
;
в) сила трения (скольжения): 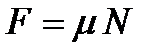 ,
,
где  коэффициент трения;
коэффициент трения; 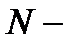 сила нормального давления.
сила нормального давления.
Закон сохранения импульса: импульс замкнутой системы остается постоянным
 .
.
Для двух тел при абсолютно упругом ударе:
 ,
,
где  и
и 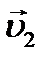 - скорости тел перед соударением,
- скорости тел перед соударением, 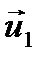 и
и 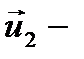 скорости тел в момент после соударения.
скорости тел в момент после соударения.
Для абсолютно неупругого удара двух тел:
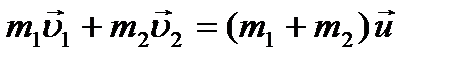 .
.
Кинетическая энергия 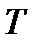 тела, движущегося поступательно:
тела, движущегося поступательно:
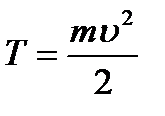 , или
, или  .
.
Потенциальная энергия  :
:
а) упругодеформированной пружины:
 ,
,
где 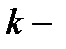 жесткость пружины;
жесткость пружины; 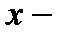 абсолютная деформация;
абсолютная деформация;
б) тела, находящегося в однородном поле силы тяжести:
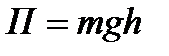 ,
,
где  ускорение свободного падения;
ускорение свободного падения; 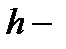 высота тела над уровнем, принятым за нулевой (формула справедлива при условии
высота тела над уровнем, принятым за нулевой (формула справедлива при условии  , где
, где 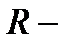 радиус Земли).
радиус Земли).
Закон сохранения механической энергии: если в системе действуют только консервативные силы, то полная механическая энергия системы не меняется
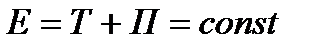 .
.
Закон сохранения энергии при абсолютно упругом столкновении двух тел, движущихся в горизонтальной плоскости:
 .
.
Закон сохранения энергии при абсолютно неупругом столкновении двух тел, движущихся в горизонтальной плоскости:
 ,
,
где  энергия нагревания тел и их остаточной деформации.
энергия нагревания тел и их остаточной деформации.
Скорости двух тел после абсолютно упругого столкновения:
 ,
,
 .
.
Работа, совершаемая результирующей силой, определяется как мера изменения кинетической энергии:
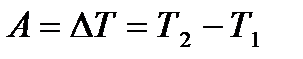 .
.
Динамика вращательного движен ия.
Основное уравнение динамики вращательного движения:
 ,
,
где 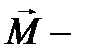 результирующий вектор моментов внешних сил, действующих на тело, относительно оси вращения;
результирующий вектор моментов внешних сил, действующих на тело, относительно оси вращения;  вектор углового ускорения;
вектор углового ускорения; 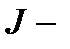 момент инерции системы относительно оси.
момент инерции системы относительно оси.
Моменты инерции некоторых тел массой  относительно оси вращения, проходящей через центр масс:
относительно оси вращения, проходящей через центр масс:
а) материальной точки: 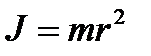 ,
,
где  расстояние от материальной точки до оси;
расстояние от материальной точки до оси;
б) стержня длиной  относительно оси перпендикулярной стержню:
относительно оси перпендикулярной стержню:
 ;
;
в) обруча или тонкостенного цилиндра радиуса R относительно оси, совпадающей с осью цилиндра:
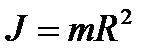 .
.
г) однородного (сплошного) диска (цилиндра) радиуса 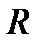 относительно оси, совпадающей с осью диска:
относительно оси, совпадающей с осью диска:
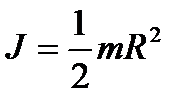 ;
;
д) пустотелого цилиндра радиусами 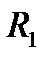 и
и 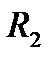 с осью вращения, совпадающей с осью цилиндра:
с осью вращения, совпадающей с осью цилиндра:
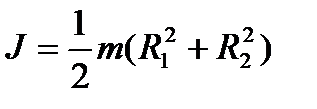 ;
;
е) шара с осью вращения, проходящей через его центр:
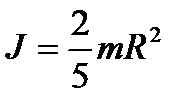 .
.
Теорема Штейнера: момент инерции 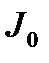 тела относительно произвольной оси равен сумме момента инерции
тела относительно произвольной оси равен сумме момента инерции  этого тела относительно параллельной оси, проходящей через центр масс, и произведения массы m на квадрат расстояния а между этими осями
этого тела относительно параллельной оси, проходящей через центр масс, и произведения массы m на квадрат расстояния а между этими осями
 ,
,
Момент импульса материальной точки массой  , имеющей скорость
, имеющей скорость 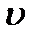 и находящуюся на расстоянии
и находящуюся на расстоянии 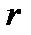 от оси вращения:
от оси вращения:
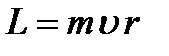 .
.
Момент импульса 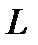 тела, вращающегося относительно неподвижной оси с угловой скоростью
тела, вращающегося относительно неподвижной оси с угловой скоростью 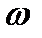 :
:
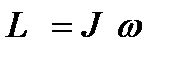 .
.
Закон сохранения момента импульса систем тел, вращающихся вокруг неподвижной оси:

 .
.
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:
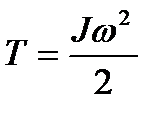 , или
, или  .
.
Кинетическая энергия катящегося тела:
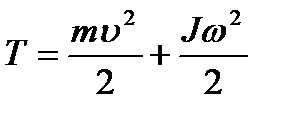 .
.
Молекулярная физика и термодинамика
Количество вещества смеси газов:
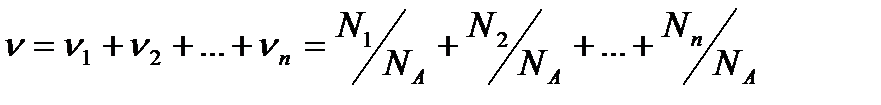 ,
,
или
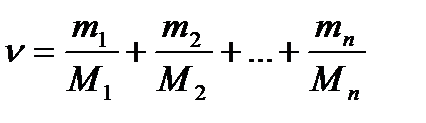 ,
,
где  соответственно – количество вещества, число молекул, масса, молярная масса
соответственно – количество вещества, число молекул, масса, молярная масса 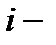 того компонента смеси.
того компонента смеси.
Уравнение Менделеева - Клапейрона (уравнение состояния идеального газа):
 ,
,
где  масса газа,
масса газа, 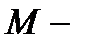 молярная масса газа,
молярная масса газа, 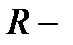 молярная газовая постоянная (
молярная газовая постоянная (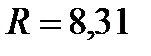 Дж/моль К),
Дж/моль К), 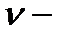 количество вещества (число молей),
количество вещества (число молей), 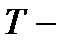 термодинамическая температура.
термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева–Клапейрона для изопроцессов:
а) закон Бойля–Мариотта (изотермический процесс:  ):
):
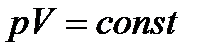 , или для двух состояний газа
, или для двух состояний газа 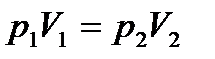 ;
;
б) закон Гей-Люссака (изобарический процесс:  ):
):
 , или для двух состояний
, или для двух состояний  ;
;
в) закон Шарля (изохорический процесс:  ):
):
 , или для двух состояний
, или для двух состояний 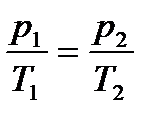 ;
;
г) объединенный газовый закон ( ):
):
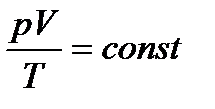 , или
, или 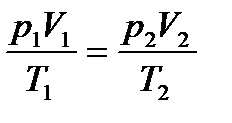 ,
,
где  давление, объем и температура газа в начальном состоянии;
давление, объем и температура газа в начальном состоянии; 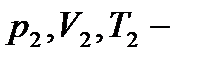 те же величины в конечном состоянии.
те же величины в конечном состоянии.
Закон Дальтона, определяющий давления смеси газов:
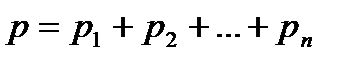 ,
,
где 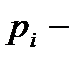 парциальные давления компонентов смеси;
парциальные давления компонентов смеси; 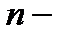 число компонентов смеси.
число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы он только один находился в сосуде, занятом смесью.
Молярная масса смеси газов:
M= 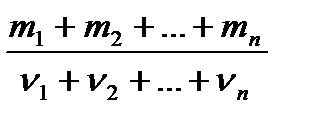 ,
,
где  масса
масса 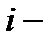 того компонента смеси;
того компонента смеси; 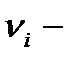 количество вещества
количество вещества 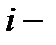 того компонента смеси;
того компонента смеси;  число компонентов смеси.
число компонентов смеси.
Массовая доля 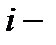 того компонента смеси газа (в долях единицы или процентах):
того компонента смеси газа (в долях единицы или процентах):
 ,
,
где  масса смеси.
масса смеси.
Концентрация молекул:
 ,
,
где  число молекул вещества, содержащихся в системе;
число молекул вещества, содержащихся в системе; 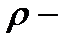 плотность вещества;
плотность вещества; 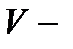 объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
объем системы. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.
Основное уравнение кинетической теории газов:
 ,
,
где  постоянная Больцмана.
постоянная Больцмана.
Средняя кинетическая энергия поступательного движения молекулы:
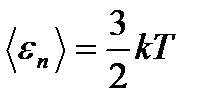 ,
,
Средняя полная кинетическая энергия молекулы:
 ,
,
где 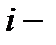 число степеней свободы молекулы.
число степеней свободы молекулы.
Скорости молекул:
 средняя квадратичная;
средняя квадратичная;
 средняя арифметическая;
средняя арифметическая;
 наиболее вероятная,
наиболее вероятная,
где  масса одной молекулы.
масса одной молекулы.
Теплоемкость C определяется количеством тепла Q, которое надо подвести к системе, чтобы увеличить ее температуру на 1 К
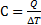 .
.
Теплоемкость – функция процесса. Она зависит от того, как нагревался газ: при постоянном объеме или при постоянном давлении.
Удельные теплоемкости газа при постоянном объеме 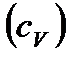 и постоянном давлении
и постоянном давлении  , имеющего
, имеющего  степеней свободы:
степеней свободы:

 ,
,  .
.
Связь между молярной и удельной теплоемкостями:
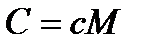 .
.
Уравнение Майера: 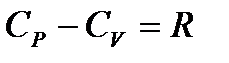 .
.
Внутренняя энергия идеального газа:
 .
.
Первое начало термодинамики: теплота, подведенная к системе, идет на изменение ее внутренней энергии и на совершение работы против внешних сил
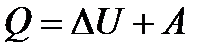 ,
,
где 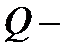 теплота, сообщенная системе (газу);
теплота, сообщенная системе (газу); 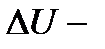 изменение внутренней энергии системы;
изменение внутренней энергии системы;  работа, совершенная системой против внешних сил.
работа, совершенная системой против внешних сил.
Работа расширения газа:
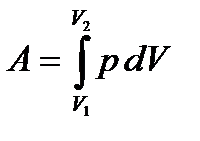 в общем случае;
в общем случае;
 при изобарном процессе;
при изобарном процессе;
 при изотермическом процессе;
при изотермическом процессе;
 при адиабатном процессе, где
при адиабатном процессе, где  показатель адиабаты.
показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
 .
.
Контрольная работа № 1.