ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Измерить какую-либо величину - значит сравнить ее с однородной величиной, принятой за единицу измерения.
Различают прямые измерения и косвенные.
Прямыми называются измерения, цель которых состоит в определении измеряемой величины непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах.
Косвенными называются измерения, при которых искомая величина определяется по результатам прямых измерений других величин, связанных с этой величиной определенной функциональной зависимостью.
Измерения любых величин не могут быть абсолютно точными по разным причинам. Поэтому результаты измерений дают не истинное, а приближенное значение измеряемой величины. Погрешности или ошибки, возникающие при измерениях, делятся на группы: систематические, случайные и промахи.
| Таблица 1 | ||
| Вид погрешностей | Возможные источники | Способы устранения |
| Систематические - погрешности, которые остаются постоянными. | Неточность метода измерения | Переход к более совершенному методу измерения Регулировка прибора Введение поправок к его шкале Повысить качество разработки теории опыта |
| Недостаточно полный учет факторов, влияющих на измеряемую величину Измерительная аппаратура Несовершенство теории опыта | ||
| Случайные - это погрешности, появление которых невозможно предупредить. | Ограниченность чувствительности прибора | Увеличить число измерений, при разработке результатов использовать статистические закономерности |
| Субъективные возможности экспериментатора (слух, зрение, опыт) | ||
| Изменение условий измерения | ||
| Промахи - грубые ошибки, искажающие результат измерения. | Нарушение нормальной работы измерительной аппаратуры | Выполнить повторные измерения, отбросив ошибочные данные |
| Неправильные действия экспериментатора |
В зависимости от того, с какой точностью требуется произвести измерения, используют технические или лабораторные методы.
При использовании технических методов надо произвести одно измерение. В этом случае точность измерения определяется погрешностью прибора.
Результатом измерения служит запись в виде: N=No± D N
где: No - отсчет по прибору;
D N - абсолютная погрешность измерения.
Абсолютная погрешность технического измерения равна абсолютной погрешности прибора, которая определяется исходя из класса точности прибора.
Класс точности прибора характеризует приведенная погрешность прибора eПР, которая равна отношению абсолютной D N погрешности к предельному значению NПР измеряемой величины (т.е. к ее максимальному значению по шкале прибора), выраженному в процентах:
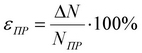
| (1) |
Приведенная погрешность прибора является по существу относительной погрешностью. По приведенной погрешности приборы делятся на:
1) технические - класса точности 1; 1,5; 2,5; 4;
2) лабораторные - класса точности 0,1; 0,2; 0,5.
Класс точности прибора указан на шкале прибора
Абсолютная погрешность, которую дает прибор, определяется из выражения (1):

|
где eПР - класс точности прибора;
NПР - предельное значение измеряемой величины по шкале прибора.
Если на шкале класс точности не обозначен, то абсолютная погрешность прибора принимается равной половине цены деления наименьшего значения шкалы прибора.
Погрешности приборов не зависят от числа измерений, они зависят от конструкции прибора. Для более точных измерений либо подбирают приборы более высокого класса точности, либо используют лабораторные методы измерений.
При лабораторных методах измерение производят n раз и получают n приближенных значений: N 1, N 2, N 3... N n.
Среднее арифметическое найденных значений принимается за наиболее достоверное значение измеряемой величины

|
Абсолютная разность между средним значением и значением отдельного измерения называется абсолютной погрешностью этого измерения:

|
Средней абсолютной погрешностью n измерений называется среднее значение абсолютных погрешностей:
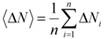
|
Истинное значение измеряемой величины будет:

| (2) |
Знаки «+» и «-» в выражении (2) означают, что погрешность может быть допущена как в сторону увеличения от действительного значения измеряемой величины, так и в сторону уменьшения.
Относительная погрешность представляет собой отношение средней абсолютной погрешности D N к среднему значению измеряемой величины < N > и выражается обычно в процентах:

|
ОЦЕНКА ПОГРЕШНОСТИ ПРИ КОСВЕННЫХ ИЗМЕРЕНИЯХ
Косвенным называется измерение данной величины a через непосредственное измерение величин X, Y, Z..., функционально связанных с первой.
Результат косвенного измерения величины a зависит от точности измерений величин X, Y, Z... и от вида функциональной связи.
В таблице 2 приведены значения абсолютной и относительной погрешностей для различного вида функциональных связей величины a, измеренной косвенно, с величинами X, Y и Z, которые измерены непосредственно.
| Таблица 2 | ||
| Вид функции | Абсолютная погрешность | Относительная погрешность |
| a=x+y+z | D a= D x+ D y+ D z | e = (D x+ D y+ D z) / (x+y+z) |
| a=x-y | D a= D x+ D y | e = (D x/x) / (D y/y) |
| a=xy | D a=xDy+yDx | e = (D x/x) + (D y/y) |
| a=xyz | D a=xy D z+xz D y+yz D x | e = (D x/x) + (D y/y) + (D z/z) |
| a=xn | D a=nxn -1D x | e =nDx/x |
| a=x1/n | D a= (1 /n) x (1 /n)-1D x | e = D x/(nx) |
| a=x/y | D a= (x D y+y D x) /y 2 | e = (D x/x) + (D y/y) |
| a= sin x | D a= D x cos x | e = D x ctg x |
| a= cos x | D a= D x sin x | e = D x tg x |
| a= tg x | D a= D x (cos2 x) | e = 2D x /sin2 x |
| a= ctg x | D a= D x (sin2 x) | e = 2D x /sin2 x |