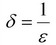При многократных измерениях физической величины N в одинаковых условиях возникают случайные погрешности - ошибки, которые вызываются большим числом неподдающихся учету случайных причин. Случайные погрешности подчиняются законам теории вероятностей.
В основе теории ошибок, применяющей методы теории вероятностей лежат 2 положения:
- случайные погрешности одинаковой величины, но разного знака равновероятны, т.е. встречаются одинаково часто;
- чем больше абсолютная величина погрешности, тем она менее вероятна, т.е. встречается значительно реже, чем малые по абсолютной величине погрешности.
Из этих положений следует, что истинное значение измеряемой величины при многократных измерениях приблизительно равно среднеарифметическому значению из этого числа измерений
При наличии случайных погрешностей появление в процессе измерения любого значения Ni является случайным событием. Существует некоторая вероятность того, что это значение N, появится в интервале [ N -D N; N+ D N ]
Пусть у - случайная ошибка измерения величины N:
Эта ошибка является непрерывной случайной величиной, которая подчиняется закону нормального распределения Гаусса:
где σ 2 - постоянная величина, называемая дисперсией распределения.
Дисперсия характеризует разброс случайных 
величин y, так как является параметром кривой распределения (рис.1). При большой дисперсии кривая расплывается, максимум становится выраженным менее ярко, более вероятны большие отклонения.
При большом числе измерений n → ∞ дисперсия σ оказывается приблизительно равной среднеквадратичной погрешности отдельного измерения:
Таким образом, чем меньше значение σ, тем точнее проведено измерение. При обработке результатов измерений в качестве предельной абсолютной погрешности отдельного измерения обычно берут величину 3 σ. Измерение считается промахом, если его абсолютная погрешность больше 3 σ.
Доверительным интервалом называют интервал [ N -D N; N+ D N ], в котором содержится истинное значение N измеряемой величины.
Обычно в лабораторных работах при небольшом числе измерений выбирается достаточная надежность 0,95.
За стандартный интервал принимается [± SX ], где
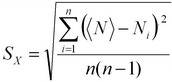
Существует специальная таблица коэффициентов Стьюдента, с помощью которых можно установить, во сколько раз следует увеличить стандартный интервал [± SX ] для того, чтобы при определенном числе измерений получить заданную надежность а (таблица 3).
Для оценки погрешности результата многократных прямых измерений существует несколько способов. Наиболее распространенным является способ, основанный на методике Стьюдента, который включает следующие действия:
1. Производят n измерений и записывают их результаты в таблицу.
2. Вычисляют среднее значение измеряемой величины по формуле:
3. Определяют среднюю квадратичную ошибку серии измерений, т.е. доверительный интервал:
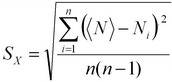
4. По таблице 3 в зависимости от заданной надежности α и числа измерений n находят коэффициент Стьюдента t (α, n).
5. Абсолютную погрешность результата серии измерений, т.е. полуширину доверительного интервала, определяют по формуле:
6. Окончательный результат записывают в виде:
Это означает, что истинное значение измеряемой величины находится в доверительном интервале [ N -D N; N+ D N ] с надежностью α.
7. Для оценки точности измерений вычисляют относительную погрешность:
Величина, обратная относительной погрешности называется точностью
