Получение формулы интеграла Мора
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим 
и 
, соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки (
) в точке K.
Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой 
(рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
Внутренние усилия, возникающие во вспомогательной балке, обозначим 
и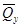 
.
Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда 
.
При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, (не учитывать второе слагаемое).
Тогда, учитывая, что , окончательно получим формулу интеграла Мора: 
.
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.
Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (
), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент 
(рис. 15.6, в).
порядок вычисления перемещений методом Мора:
· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;
· вычисляем интеграл Мора для всей балки по соответствующим участкам;
· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
Вычисление интеграла Мора пример
Пусть для шарнирно опертой балки постоянной изгибной жесткости 
, длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета (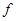
) и угол поворота на левой опоре (
).
определение прогиба с помощью интеграла Мора
В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу 
(рис. 15.7, б).
Записываем выражения для изгибающих моментов для каждого из двух участков (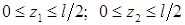
) заданной и вспомогательной балок:
.
.
Вычисляем интеграл Мора. Учитывая симметрию балки, получим:
.