СТАТИСТИКА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению расчетно-графического задания
по дисциплине: "Статистика. Часть 1"
для студентов всех специальностей дневной формы обучения
Севастополь
УДК 311(075.8)
Статистика: Методические указания по выполнению расчетно-графического задания дисциплине: "Статистика. Часть 1" для студентов всех специальностей дневной формы обучения /Сост. О.С.Доценко - Севастополь: Изд-во СевНТУ, 2005.- 21с.
Методические указания разработаны в соответствии с учебным планом и типовой программой дисциплины "Статистика" и содержат общие требования к выполнению расчетно-графического задания по дисциплине «Статистика. Часть 1», методические рекомендации по его выполнению, исходные данные по вариантам, контрольный пример и библиографический список.
Методические указания предназначены для студентов всех специальностей дневной формы обучения факультета «Экономика и менеджмент».
Методические указания рассмотрены и утверждены на заседании кафедры "Учет и аудит" СевНТУ (протокол № 1 от 29.08.05 г.).
Допущено методическим центром СевНТУ в качестве методических указаний
Рецензенты:
Кашо Т.Н.,ст. преподаватель каф. УиА;
Потанина М.В., ст. преподаватель каф. МЭМ
Содержание
Введение 4
1. Теоретическая часть………………………………………………………… 5
2. Контрольный пример…………………………………………………...…...11
3. Общие требования к выполнению расчетно-графического задания…….17
4. Контрольные вопросы……………………………………………………....18
Библиографический список………………………………………………........19
Приложение А. Исходные данные по вариантам……………………………20
|
|
ВВЕДЕНИЕ
В соответствии с учебной программой студентам дневного отделения необходимо выполнить расчетно- графическое задание по дисциплине «Статистика. Часть 1», цель которого - изучение простейших статистических методов обработки экономической информации, позволяющих получить навыки в решении определенных задач согласно требованиям.
Данные методические указания значительно упростят процесс выполнения этой работы, т.к. в них в качестве образца рассматривается контрольный пример, который ориентирует студентов на подготовку по темам: «Сводка и группировка статистических данных», «Ряды распределения», «Средние величины», «Показатели вариации».
Составляя настоящие методические указания, автор надеется на активную самостоятельную работу студентов по выполнению расчетно-графического задания. Для повышения эффективности самостоятельной работы в методических указаниях приведен теоретический материал по данным темам, подробные выкладки всех расчетных формул, требования к оформлению расчетно-графического задания, контрольные вопросы, перечень необходимой литературы.
Перед выполнением расчетно-графического задания требуется внимательное изучение настоящих методических указаний.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Для изучения предмета статистики разработаны и применяются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, группировок, обобщающих показателей, динамических рядов, индексный метод и др.). Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации. Комплексность (системность) использования статистических методов обусловлена сложностью процесса экономико- статистического исследования, состоящего из трех основных стадий: первая- сбор первичной статистической информации, где применяется метод массового статистического наблюдения; вторая - статистическая сводка и обработка первичной информации методом статистических группировок; третья- обобщение и интерпретация статистической информации, при изучении которой широкое применение имеют табличный и графический методы.
|
|
Статистические данные, обладающие некоторыми общими свойствами, характеризующие какое-либо массовое явление принятые к обработке, называются статистической совокупностью.
В расчетно – графическом задании студентам необходимо исследовать предложенную совокупность, представив данные в компактном, обозримом виде, применив метод группировок с равными интервалами, на основе которого рассчитываются и сравниваются сводные показатели по группам, анализируются причины различия между группами, изучаются взаимосвязи между признаками и закономерности развития.
Исследование статистической совокупности проводится по следующим этапам:
1-построение интервального вариационного ряда;
2-расчет числовых характеристик интервального вариационного ряда;
3-графическое изображение интервального вариационного ряда (гистограмма, полигон, кумулята);
4-экономическая интерпретация результатов статистической обработки данных.
|
|
1 этап-построение интервального вариационного ряда
Имеющиеся в распоряжении исследователя исходные данные располагают в виде ранжированного дискретного вариационного ряда (т.е. ряда распределения, построенного по количественному признаку, в котором варианты (значения признаков) – целые числа). Он представляет собой таблицу, в которой показатели располагаются в порядке возрастания (или убывания) значений и называется первичным рядом распределения. Далее, используя метод равных группировок, переходят от дискретного вариационного ряда к интервальному вариационному ряду распределения (ряду распределения, построенному по количественному признаку, в котором варианты даны в виде интервалов и могут принимать в этих интервалах любые значения).Число групп или интервалов (n) определяется по формуле американского ученого Стерджесса (стандартизированный подход):
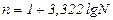, (1.1)
где n -число групп,
N- количество единиц всей совокупности.
Для группировок с равными интервалами размер интервала (i) определяется по формуле:
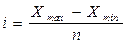, (1.2)
где Xmax – наибольшее значение варьирующего признака;
Xmin - наименьшее значение варьирующего признака.
Если в результате деления получается дробное число, округление производят в большую сторону (это делается для того, чтобы максимальное значение совокупности Xmax попало в последний интервал).
Прибавляя к наименьшему значению признака найденное значение интервала, получаем верхнюю границу первой группы; прибавляя далее величину интервала к верхней границе первой группы, получаем верхнюю границу второй группы и т.д., пока наибольшее значение признака не окажется либо равным, либо несколько меньше значения верхней границы последней группы. Определив частоты (количество вариантов, попавших в каждую группу), получим интервальный вариационный ряд. В случае совпадения варианта со значением границы интервала (т.е. в случае неопределенности отнесения значения признака к тому или иному интервалу), используют принцип единообразия: левое число интервала включает в себя обозначенное значение, а правое – не включает, т.е. данный вариант переходит в следующий интервал.
2 этап-расчет числовых характеристик интервального вариационного ряда.
Для правильного представления о характере распределения, студентам необходимо рассчитать следующие числовые характеристики интервального вариационного ряда:
1. Частости (w) по всем группам.
2. Абсолютную (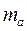
) и относительную (
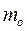) плотности распределения по
всем группам.
3. Среднее значение признака (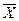
).
4. Медиану Me.
5. Моду Mo.
6. Общую дисперсию 
, межгрупповую дисперсию 
,
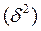внутригрупповую дисперсию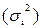 
.
7. Среднее квадратическое отклонение (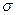
).
8. Коэффициент вариации (V).
9. Эмпирический коэффициент детерминации(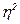
).
10.Эмпирическое корреляционное отношение (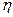
).
Дадим определение этих понятий и приведем формулы расчета данных показателей.
Частость ( w) -частота, выраженная в долях единиц или в процентах к итогу. (Сумма частостей равна 1 или 100%):
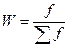, (1.3)
где f - частота.
Сумма всех частот равна численности всей совокупности.
Абсолютная плотность распределения (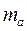) - частота, отнесенная к ширине интервала:
= 
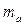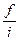. (1.4)
Относительная плотность распределения (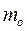) - частость, отнесенная к ширине интервала:
= 
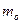. (1.5)
Расчет абсолютной и относительной плотности распределения обычно производится для вариационного ряда с неравными интервалами. Эти показатели используют для перегруппировки данных с целью получения сопоставимых интервалов и дальнейшего их анализа.
Средней величиной (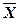
) называют статистический показатель, который дает обобщенную характеристику варьирующего признака единиц однородной совокупности. Под качественной однородностью единиц совокупности понимается сходство единиц (объектов, явлений) по каким-либо существенным признакам, но различающихся по каким- либо другим признакам.
При нахождения средней величины в интервальном ряду распределения, истинные значения признака заменяются центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал. Вычисления производят по формуле средней арифметической взвешенной:
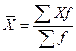, (1.6)
где Х -центральные значения интервалов.
Медиана - это вариант, находящийся в середине ранжированного вариационного ряда.
В интервальном вариационном ряду распределения медиана определяется после предварительного нахождения медианного интервала, т.е. интервала, накопленная частота которого (кумулятивная частота) равна или впервые превышает полусумму всех частот ряда по формуле:
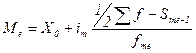, (1.7)
где Х0 – начальное значение интервала, содержащего медиану;
im - величина медианного интервала;
- сумма частот ряда;
Sme-1 –накопленная частота интервала, предшествующего медианному;
fmе – частота медианного интервала.
Мода - наиболее часто встречающийся вариант дискретного ряда распределения, т.е. вариант, имеющий наибольшую частоту.
В интервальном ряду распределения приблизительной модой считают центральный вариант так называемого модального интервала, т.е. интервала, имеющего наибольшую частоту или частость. В этом случае мода определяется так:
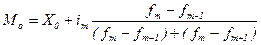, (1.8)
где Х0 –нижняя граница модального интервала;
im - величина модального интервала;
fm - частота модального интервала;
fm-1 – частота интервала, предшествующего модальному;
fm+1 – частота интервала, следующего за модальным.
Общая дисперсия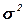 
измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию, и вычисляется по формуле:
. (1.9)
Межгрупповая дисперсия 
- характеризует систематическую вариацию результативного признака, обусловленную влиянием признака- фактора, положенного в основание группировки.
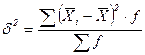, (1.10)
где 
- групповые средние;
- общая средняя,
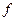-численность единиц в i-той группе.
Внутригрупповая дисперсия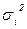 
-дисперсия в пределах каждой группы, которая отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки:
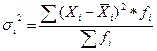, (1.11)
где 
-частота варианта 
,
-варианты внутри групп.
На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:
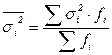, (1.12)
где - численность единиц в i-той группе.
Согласно правилу сложения дисперсий:
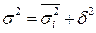. (1.13)
Использование центральных значений интервалов для вычисления общей средней 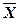заданного распределения приводит к систематической погрешности при расчете общей и межгрупповой дисперсий. В силу этого равенство между значениями 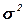, определяемыми по формулам (1.9) и (1.13) будет приблизительным. Поэтому в расчетно-графическом задании студентам необходимо вычислять общую дисперсию, используя только формулы (1.10-1.13).
При расчете дисперсии не указываются единицы измерения.
Среднее квадратическое отклонение (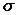
) - это обобщающая характеристика размеров вариации признака в совокупности, оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения и выражается в тех же единицах, что и варианты:
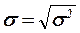. (1.14)
Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина
Коэффициент вариации ( V) - выраженное в процентах отношение среднего квадратического отклонения к средней:
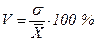. (1.15)
Коэффициент вариации используют для сравнительной оценки вариации различных признаков в одной совокупности; для сравнений колеблемости одного и того же признака в нескольких совокупностях; для характеристики однородности совокупности.
Если коэффициент вариации меньше 33 %, то это значит, что совокупность количественно однородна, а средняя для нее типична.
Эмпирический коэффициент детерминации(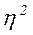
) - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
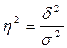. (1.16)
При отсутствии связи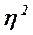 
=0, а при функциональной связи 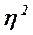=1.
Эмпирическое корреляционное отношение (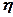
)- (показатель Пирсона)- показывает тесноту связи между группировочным и результативным признаками.
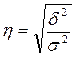. (1.17)
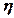принимает значения от 0 до 1.
Если связь отсутствует, то 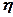=0, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет.
Если связь функциональная, то корреляционной отношение будет равно единице. В этом случае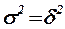 
, т.е внутригрупповой вариации не будет.
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками (см. таблицу 1.1).
Таблица 1.1- Сила связи в зависимости от значения показателя Пирсона(соотношения Чэддока)
| Значения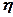
| Сила связи |
| 0,1-0,3 | слабая |
| 0,3-0,5 | умеренная |
| 0,5-0,7 | заметная |
| 0,7-0,9 | тесная |
| 0,9-0,99 | весьма тесная |
3-этап графическое изображение интервального вариационного ряда.
Графические методы в статистике являются способом наглядного изображения результатов статистической сводки и обработки массового материала. На этом этапе студентам необходимо проанализировать полученный ряд распределения, построив гистограмму, полигон и кумуляту.
Гистограмма распределения применяется чаще всего для изображения интервальных рядов. Для ее построения по оси абсцисс откладываются интервалы признака, а по оси ординат - численности единиц совокупности. На отрезках, изображающих интервалы, строят прямоугольники, площади которых пропорциональны численностям единиц.
Полигон строят в основном для изображения дискретных рядов. При его построении на оси абсцисс откладываются значения варьирующего признака, а на оси ординат - абсолютные или относительные численности единиц совокупности (частоты или частости). При построении полигона для интервального ряда переходят к дискретному ряду, заменяя интервалы центральными (серединными) значениями варьирующего признака.
При построении кумуляты значения варьирующего признака откладываются на оси абсцисс, а на оси ординат помещаются накопленные итоги частот или частостей. При построении кумуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней – накопленная частота данного интервала; нижней границе второго интервала соответствует накопленная частота первого интервала, а верхней- накопленная частота второго интервала и т.д.
КОНТРОЛЬНЫЙ ПРИМЕР
Задание
Имеются данные о размере заработной платы рабочих комплексной бригады (см. таблицу 2.1). Исследовать исходные данные, применив метод группировок с равными интервалами. Произвести расчет основных характеристик полученного ряда распределения. Объяснить полученные результаты. Построить гистограмму, полигон и кумуляту распределения. Найти моду и медиану графическим способом.
Таблица 2.1-Данные о размере заработной платы 30 рабочих комплексной бригады, ден.ед.
Этапы обработки данных
1. Построение интервального вариационного ряда.
Исходные данные располагают в виде первичного ранжированного дискретного вариационного ряда (см. таблицу 2.2).
Таблица 2.2- Первичный ранжированный дискретный вариационный ряд
Используя метод равных группировок (интервалов), переходят от дискретного вариационного ряда к интервальному, определив количество групп (интервалов) по формуле Стерджесса (1.1):
.
Из формулы (1.2)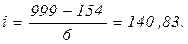 
После разбивки диапазона значений варьирующего признака на интервалы определяется количество данных, попавших в каждый из них.
Для дискретного ряда, приведенного в таблице 2.2, интервальный вариационный ряд представлен в таблице 2.3 (см. 1 и 4 столбцы).
Таблица 2.3 –Группировка работников по заработной плате
| Группы работников по з/п | Значение заработной платы, ден.ед,
( )
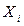| Середина интервала, ден.ед. (Х) | Количество рабочих, чел (f) | Х*f |
| 154,00-294,83 | 154, 201, 214, | 224,415 | 673,245 | |
| 294,83-435,66 | 302, 320, 320, 324, 325, 329, 357 | 365,245 | 2556,715 | |
| 435,66-576,49 | 478, 517, 548, 558 | 506,075 | 2024,300 | |
| 576,49-717,32 | 605, 615, 658, 658, 698 | 646,905 | 3234,525 | |
| 717,32-858,15 | 745, 754, 754 | 787,735 | 2363,205 | |
| 858,15-999,00 | 865, 896, 875, 878, 950, 968, 985, 999, | 928,575 | 7428,600 | |
| итого | Х | Х | 18280,590 |
2. Расчет числовых характеристик интервального вариационного ряда.
Используя формулы (1.3-1.5), рассчитывают частости и плотности распределений по группам. Результаты заносят в дополнительную таблицу 2.4 (см. 5, 6, 7 столбцы).
Таблица 2.4 (дополнительная) – Группировка работников по заработной плате
| Группы работников по з/п | Середина интервала, ден.ед. (Х) | Количество рабочих, чел. (f) | Накоплен- ная частота, чел. (S) | Час- тость,% (w) | Плотность абсолют-ная,
( )
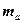| Плотность относитель-ная,
( )
|
| 154,00-294,83 | 224,415 | 10,0 | 0,0213 | 0,00071 | ||
| 294,83-435,66 | 365,245 | 23,3 | 0,0497 | 0,00166 | ||
| 435,66-576,49 | 506,075 | 13,3 | 0,0284 | 0,00095 | ||
| 576,49-717,32 | 646,905 | 16,7 | 0,0355 | 0,00118 | ||
| 717,32-858,15 | 787,735 | 10,0 | 0,0213 | 0,00071 | ||
| 858,15-999,00 | 928,575 | 26,7 | 0,0568 | 0,00189 | ||
| итого | Х | Х | 100,0 | Х | Х |
Среднюю заработную плату рассчитывают по формуле (1.6), с использованием промежуточных расчетов в таблице 2.3 (см. 5 столбец):
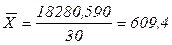(ден.ед.).
Моду и медиану для интервального вариационного ряда рассчитывают по формулам (1.7-1.8), определив предварительно модальный и медианный интервалы. Модальный интервал-(858,15-999,00), т.к. частота этого интервала (f =8) максимальная. Медианный интервал-(576,49-717,32), т.к. накопленная частота этого интервала впервые превышает полусумму всех частот ряда распределения (S=19,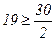 
).
Тогда:
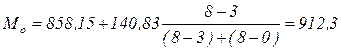(ден.ед).
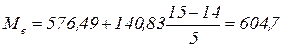(ден.ед).
Межгрупповую дисперсию найдем табличным способом (см. таблицу 2.5),
воспользовавшись формулой (1.10).
Таблица 2.5-Расчетные значения для вычисления межгрупповой дисперсии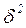 
| Группы |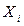
| Х |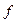 
|
| 
| 
| 
|
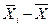
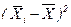
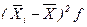
| 154,00-294,83 | 154, 201, 214 | 224,415 | 189,67 | -419,73 | 176173,3 | 528519,9 | |
| 294,83-435,66 | 302, 320, 320, 324, 325, 329, 357 | 365,245 | 325,29 | -284,11 | 80718,5 | 565029,5 | |
| 435,66-576,49 | 478, 517, 548, 558 | 506,075 | 525,25 | -84,15 | 7081,2 | 28324,8 | |
| 576,49-717,32 | 605, 615, 658, 658, 698 | 646,905 | 646,80 | 37,40 | 1398,8 | 6994,0 | |
| 717,32-858,15 | 745, 754, 754 | 787,735 | 751,00 | 141,60 | 20050,6 | 60151,8 | |
| 858,15-999,00 | 865, 896, 875, 878, 950, 968, 985, 999, | 928,575 | 927,00 | 317,60 | 100869,8 | 806958,4 | |
| итого | Х | Х | Х | Х | Х | 1995978,4 |
.
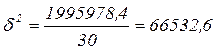Для расчета внутригрупповых дисперсий по группам воспользуемся формулой (1.11):
,
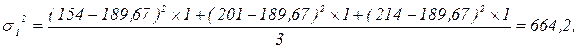
аналогично рассчитываем: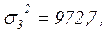 
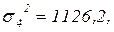
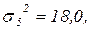
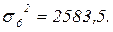
Вычислим среднюю из внутригрупповых дисперсий, используя формулу (1.12):
.
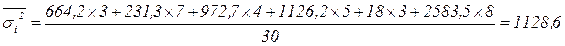По правилу сложения дисперсий (см. формулу 1.13):
.
Используя формулы (1.14-1.15), найдем коэффициент вариации:
.
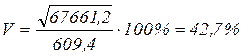Долю вариации результативного признака под влиянием факторного вычислим с помощью эмпирического коэффициента детерминации (см. формулу 1.16):
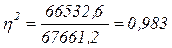(или 98,3 %).
Теснота связи между группировочным и результативным признаками (показатель Пирсона) (см. формулу 1.17):
.
   |
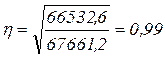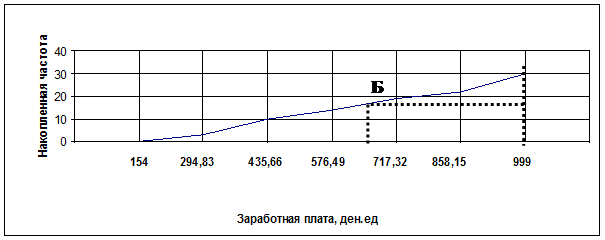
3 Графическое изображение интервального вариационного ряда.
а)
 |  | ||
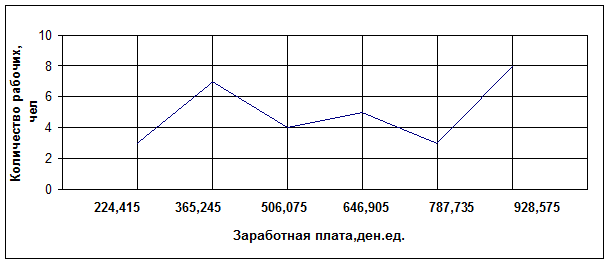б)
в)
Рисунок 3.1- Распределение заработной платы по числу рабочих бригады:
а) гистограмма,
б) полигон,
в) кумулята
Абсцисса точки А (см. рисунок 3 (а)) является модой распределения. Абсцисса точки Б (см. рисунок 3 (в))- медиана распределения.
4. Экономическая интерпретация результатов статистической обработки данных.
Таким образом, исследовав информацию о заработной плате у рабочих комплексной бригады с помощью простейших статистических методов, можно сделать следующие выводы по полученным числовым характеристикам:
1) Разброс заработной платы достаточно значителен (т.е. разница между максимальным и минимальным значениями совокупности): от 154 (ден.ед.) до 999 (ден.ед.). Очевидно, что это связано с различием в квалификации рабочих комплексной бригады.
2) Размер средней заработной платы одного рабочего, являющийся обобщенной характеристикой заработных плат каждого рабочего в совокупности, равен 609,4 (ден.ед.).
3) Приблизительное значение медианы 604,7 (ден.ед) получилось ниже (604,7<609,4) этого значения. Это говорит о том, что половина всех сотрудников работают с заработной платой чуть ниже средней.
4) Наиболее часто встречающаяся заработная плата, определенная с помощью моды, приблизительно равна 912,3 ден. ед.
5) Коэффициент вариации больше 33 % (42,7 %), поэтому совокупность количественно неоднородная, а величина средней заработной платы на одного рабочего нетипичная.
6) Общая дисперсия, отражающая суммарное влияние всех возможных факторов (стаж работы, квалификация, характер работы, болезни и т.д.) на общую вариацию средней зарплаты всех рабочих бригады равна 67661,2.
7) Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификации, и равна 66532,6.
8) Внутригрупповые дисперсии показывают вариации заработной платы в каждой группе, вызванные всеми возможными факторами, кроме различий в квалификации. Средняя из внутригрупповых дисперсий равна 1128,6.
9) Эмпирический коэффициент детерминации равен 98,3 %. Это означает, что на 98,3 % вариация в совокупности обусловлена различиями в квалификации (а, следовательно, и в заработной плате) у рабочих и на 1,7 %- влиянием прочих факторов.
10) Эмпирическое корреляционное отношение равно 0,99. Это значит, что сила связи между квалификацией (группировочным признаком) и заработной платой (результативным признаком) весьма тесная.
Т.к. исследование совокупности проводилось с использованием метода равных группировок, то такие характеристики как абсолютная и относительная плотности распределения рассчитываются лишь как основные характеристики интервального вариационного ряда распределения без дальнейшего их применения.
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКОГО ЗАДАНИЯ
Расчетно-графическое задание должно быть оформлено на листах формата А-4 с указанием на титульном листе названия кафедры, темы работы; группы, фамилии и инициалов выполнившего работу; фамилии, инициалов и должности принявшего работу. Студент выполняет задачу с исходными данными по своему варианту (см. приложение А). Номер варианта выбирается по списку из журнала преподавателя.
Отчет должен содержать:
1. Цель работы.
2. Исходные данные (см. приложение А).
3. Порядок выполнения расчетов:
а) построение интервального вариационного ряда;
б) расчет числовых характеристик вариационного ряда:
· накопленных частот по группам,
· частостей по группам,
· абсолютной плотности распределения по группам,
· относительной плотности распределения по группам
· средней арифметической,
· моды,
· медианы,
· внутригрупповых, межгрупповой и общей (по правилу сложения) дисперсий,
· коэффициента вариации,
· эмпирического коэффициента детерминации,
· эмпирического корреляционного отношения,
в) графики гистограммы, полигона и кумуляты.
4. Экономическую интерпретацию результатов статистической обработки данных.
Необходимые расчеты должны быть оформлены в таблицах (см. пункт 2-контрольный пример) с соблюдением правила их построения: каждая таблица оформляется заголовком и итоговой строкой, соблюдаются одинаковые приближения в расчетах по показателям, все клетки таблицы должны быть заполнены.
При вычислении статистических показателей необходимо указывать их единицы измерения (если они есть). Расчеты межгрупповой, всех внутригрупповых, средней из внутригрупповых дисперсий должны быть приведены полностью без сокращений.
Графики необходимо оформлять как рисунки с указанием названий и единиц измерений осей координат.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дать определение статистической совокупности.
2. Качественно однородная совокупность. Примеры.
3. Сущность группировок. Их виды.
4. Понятие ряда распределения. Его основные элементы.
5. Виды рядов распределения.
6. Способы графического представления рядов распределения.
7. Относительная и абсолютная плотности распределения. Необходимость их расчета.
8. Средняя величина. Ее виды.
9. Понятие моды. Определение моды в дискретном и интервальном рядах распределения.
10. Понятие медианы. Определение медианы в дискретном и интервальном рядах распределения.
11. Вариация признака. Основные показатели вариации.
12. Количественно однородная совокупность.
13. Сущность дисперсии. Характеристика общей, межгрупповой и внутригрупповой дисперсий.
14. Правило сложения дисперсий.
15. Эмпирический коэффициент детерминации.
16. Эмпирическое корреляционное отношение.