U – критерий Манна – Уитни.

Критерий предназначен для оценки различий между двумя выборками по уровню какого-либо количественно измеренного признака, при распределении вариант отличном от нормального. Более того, он позволяет выявлять различия между малыми выборками (когда n₁, n₂³3 или n₁=2, n₂³5). Этот метод определяет насколько слабо перекрещиваются (совпадают) значения между двумя выборками. Чем меньше перекрещивающихся значений, тем более вероятно, что различия достоверны.

Чем меньше U_эмп тем более вероятно, что различия достоверны.

Нулевая гипотеза: уровень признака в выборке 2 не ниже уровня признака в выборке 1.

Прежде чем проводить оценку критерием U необходимо провести ранжирование.

ОПРЕДЕЛЕНИЕ: Ранжирование – распределение вариант внутри вариационного ряда от меньших величин к большим.

Правила ранжирования:

1. Меньшему значению начисляется меньший ранг, как правило, это 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений (если n=10, то наибольшее значение получит ранг 10).

2. Если несколько значений равны, им начисляется ранг, представляющийсобой среднее значение из тех рангов, которые они получили бы, если бы не были равны:

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле: , где N- общее количество ранжируемых значений. Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. Прежде чем продолжить работу, необходимо найти ошибку и устранить ее.

Пример.

Проранжируем следующий ряд.

Варианты	Ранг
	2,5           2,5	Ранг 11 равен 1. Варианта 12 встречается дважды, ему начисляется ранг, представляющийсобой среднее значение из тех рангов, которые они получили бы, если бы не были равны: . Следовательно значению 12 соответствует ранг 2,5. Значению 13 соответствует ранг 4. Соответственно, значениям 14,15, 16 присваиваются ранги 5, 6, 7.

По формуле проверим правильность ранжирования.

. Определим сумму рангов: 1+2,5+2,5+4+5+6+7=28.

Общая сумма рангов совпадает с расчетной. Следовательно мы правильно проранжировали.

Схема подсчета критерия Манна-Уитни:

1. Создать таблицу. (1 столбец – одна сравниваемая группа, 2 столбец – вторая).
2. Проранжировать значения вариант в обоих столбцах (как если бы работали с одной большой выборкой).
3. Подсчитать сумму рангов для первого и второго столбцов отдельно. Проверить, совпадает ли общая сумма рангов с расчетной.
4. Определить большую из двух ранговых сумм.
5. Определить значение U_эмп по формуле: 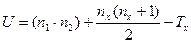, где n₁- количество вариант в выборке 1; n₂- количество вариант в выборке 2; Т_х – большая из ранговых сумм; n_x – количество вариант в группе с большей суммой рангов.
6. Определить критические значения U_кр по таблице. Если U_эмп >U_кр, нулевая гипотеза принимается. Если U_эмп ≤U_кр, нулевая гипотеза отвергается.

Чем меньше значения U, тем достоверность различий выше и тем больше уверенности в отклонении нулевой гипотезы.

3 пример.

При заболеваниях сетчатки повышается проницаемость ее сосудов. Исследователи измерили проницаемость сосудов сетчатки у здоровых и у больных с ее поражением. Полученные результаты приведены в таблице.

Проверить, подтверждают ли эти данные гипотезу о различии в проницаемости сосудов сетчатки.

Нулевая гипотеза: проницаемость сосудов сетчатки при заболеваниях сетчатки у больных не больше, чем у здоровых, (нет статистического различия между двумя выборками).

Альтернативная гипотеза: проницаемость сосудов сетчатки при заболеваниях сетчатки у больных больше, чем у здоровых, (есть статистическое различие между двумя выборками).

Здоровые	больные
проницаемость сосудов сетчатки	Порядковый номер	Ранг	проницаемость сосудов сетчатки	Порядковый номер	Ранг
0,5			1,2		6,5
0,7		2,5	1,4
0,7		2,5	1,6
1,0		4,5	1,7
1,0		4,5	1,7
1,2		6,5	1,8
1,4			2,2		18,5
1,4			2,3
1,6			2,4
1,6			6,4
1,7
2,2		18,5	23,6

,

Формула расчета критерия имеет вид:

.

.

В нашем случае , следовательно, нулевая гипотеза отвергается и можно сделать вывод о достоверности различия проницаемости сосудов сетчатки у здоровых и у больных с ее поражением.