Линейную функцию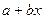 
ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значениям используем метод наименьших квадратов.
 |
 |
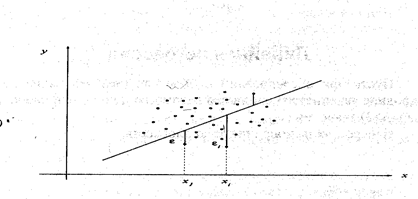
Рис.4. Пояснение к оценке коэффициентов методом наименьших квадратов
Обозначим: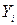 
- значение, вычисленное по уравнению 
- измеренное значение,
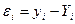- разность между измеренными и вычисленными по уравнению значениям,
.
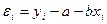В методе наименьших квадратов требуется, чтобы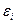 
, разность между измеренными и вычисленными по уравнению значениям 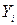, была минимальной. Следовательно, находимо подобрать коэффициенты а и 
так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:
.
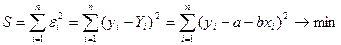Это условие достигается если параметры а и будут вычислены по формулам:
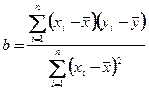(2)
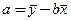(3)
называют коэффициентом регрессии;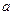 
называют свободным членом уравнения регрессии.
Полученная прямая является оценкой для теоретической линии регрессии. Имеем
.
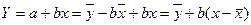Итак,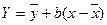 
является уравнением линейной регрессии.
Регрессия может быть прямой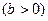 
и обратной 
.
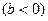ОПРЕДЕЛЕНИЕ: Обратная регрессия означает, что при росте одного параметра, значения другого параметра уменьшаются.
ОПРЕДЕЛЕНИЕ: Прямая регрессия означает, что при росте одного параметра, значения другого параметра тоже увеличиваются.
Пример.Заданному уровню потребления пресной воды на санитарно – бытовые нужды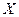 
в л/чел. сутки в n населенных пунктах соответствует множество значений уровня общей заболеваемости 
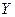в %. При этом отмечается, что с ростом 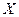наблюдается уменьшение 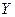. Это – обратная, отрицательная корреляционная связь. (Рис. 5)
Пример 2.Возрастание уровня инфекционной заболеваемости 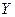в % при увеличении плотности рабочих мест в производственном помещении 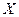, чел. – является примером прямой, положительной корреляционной связи. (Рис. 6)
 |
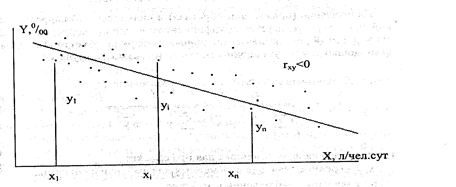Рис. 5. Поле наблюдений
при обратной корреляционной
связи между фактором 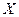и параметром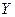
 |
Рис. 6. Поле наблюдений
при прямой корреляционной
связи между фактором и параметром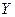
Проверка гипотезы о значимости коэффициента регрессии.
Не всегда можно утверждать, что предполагаемая линейная зависимость действительно имет место.
Построив модель, описывающую изменения величин, необходимо определить верна ли она.
В регрессионном анализе проверяют гипотезы о значимости свободного члена а и о значимости коэффициента регрессии .
1. Определяем гипотезы H0 и H1:
H0: =0 (между величинами нет линейной зависимости),
H1: ≠0 (между величинами есть линейная зависимость)
2. Зададим уровень значимости α.
3. Статистика критерия.
, где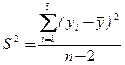 
4. Критические точки и критическая область. Статистика F имеет распределение Фишера с 1 и (n-2) степенями свободы. Fα,1,n-2
5. Если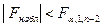 
, то H0 отвергается, т.е. можно сделать вывод, что линейная зависимость значима.
Если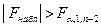 
, то у нас нет оснований отвергать H0, т.е. можно сделать вывод, что линейная зависимость – незначима или что данные нельзя описать моделью линейной регрессии.
Корреляционный анализ.
Для достаточно полного описания особенностей корреляционной зависимости между величинами недостаточно определить форму этой зависимости и в случае линейной зависимости описать ее вид по величине коэффициента регрессии. Необходимо так же оценить тесноту связи.
Корреляционный анализ экспериментальных данных для двух случайных величин заключает в себе следующие основные приемы:
1. Вычисление выборочных коэффициентов корреляции.
2. Составление корреляционной таблицы.
3. Проверка статистической гипотезы значимости связи.
Линейная корреляция
ОПРЕДЕЛЕНИЕ: Корреляционная зависимость между случайными величинами Х и 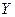называется линейной корреляцией, если обе функции регресси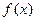и 
и 
являются линейными. В этом случае обе линии регрессии являются прямыми; они называются прямыми регрессии.