Параболический цилиндр (ПЦ) возбуждается линейным облучателем, располагающемся вдоль фокальной линии зеркала FF´ (рис. 5) и имеющем длину, приблизительно равную длине образующей цилиндра dг, причем dг >> λ.
Линейный облучатель конечных размеров на небольших расстояниях от себя создает цилиндрическую волну, имеющую две основные зоны:
1) ближнюю, находящуюся в непосредственной близости от облучателя;
2) квазидальнюю, расположенную на расстояниях r, которые удовлетворяют неравенству λ < r < dг2/λ; квазидальняя зона является областью, в пределах которой волна, создаваемая линейным облучателем, является цилиндрической.
Рис. 3. Параболический цилиндр
Для нормальной работы зеркала необходимо, чтобы оно находилось в зоне действия цилиндрической волны, создаваемой облучателем, т.е. в квазидальней зоне. Это условие равносильно выполнению следующих неравенств: dг >> λ; f >> λ; ρ0 < dг2/λ.
Исходными данными для расчета цилиндропараболической антенны являются: ширина диаграммы направленности в горизонтальной плоскости 2j0Р/2, в вертикальной плоскости 2q0Р/2, длина волны l, мощность излучения РS.
В качестве облучателя применяется линейный облучатель, формирующий цилиндрический фронт волны (рис. 6).
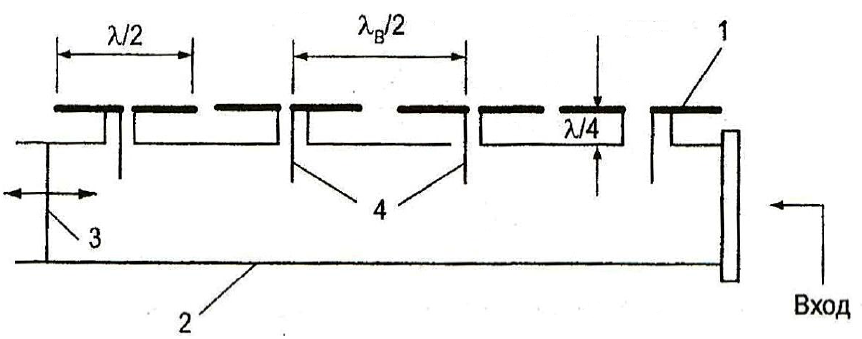
Рис. 4. Линейный облучатель
В сантиметровом диапазоне облучатель с вибраторами 1 возбуждают волноводом 2. Короткозамыкатель 3, установленный в конце секции волновода, необходим для настройки облучателя. Штыри 4 являются приемными антеннами и служат для отбора мощности и передачи ее на входы вибраторов.
По заданной длине волны определяются ориентировочные размеры прямоугольного волновода:
| a' = λ/1,4; b’ = (0,3..0,5)а' | (3.1) |
a' = λ/1,4 = 4,5/1,4 = 3,2 см
b’ = (0,3..0,5)а' = 1,6 см
По найденным значениям подбираем прямоугольный волновод МЭК-70 с размерами a = 34,85 мм; b = 15,799 мм и проверяем его на допустимую мощность:
| (3.2) |
Рпред = 3,485∙1,5799∙455,16 = 2506 кВт
Рассчитываем количество вибраторов в ряду:
| (3.3) |
n = 102∙0,76/8 = 10
Ток пучности вибратора
| (3.4) |
In = (2∙50000/32)1/2 = 55,9 А.
По величине критического напряжения Екр = 30 кВ/см у поверхности вибратора определяется радиус вибратора:
| (3.5) |
Таким образом принимаем: r = 0,3 см.
Волновое сопротивление вибратора:
| (3.6) |
W = 120∙(ln4,775 – 0,578) = 118,2 Ом
Определяем укорочение вибраторов:
| (3.7) |
Dl = 4,5∙6,6/(3,14∙118,2∙10) = 0,183 мкм
Диаграмма направленности в плоскости Н рассчитывается по формуле
| (3.8) |

Рис. 5. Диаграмма направленности в плоскости Н
По диаграмме направленности облучателя находится амплитудное распределение тангенциальной составляющей напряженности электрического поля в раскрыве антенны:
| (3.9) |

Рис. 6. График Е(j)
По графику Е(j) определяется угол раскрыва зеркала 2y0, при котором плотность потока мощности составляет 0,1..0,2 от максимума, что соответствует значению 0,316..0,447 по напряженности (от значения Е(0) в направлении максимума излучения.
Определяется размер зеркала в плоскости Н.
| (3.10) |
LH = 68∙4,5/2 = 152 см
Определяется фокусное расстояние параболического цилиндра
| (3.11) |
f = 152∙ctg(0,65)/4 = 49,8 см
Определяется форма сечения параболического отражателя
| (3.12) |

Рис. 7. Форма сечения отражателя
Определяется длина параболического цилиндра:
| (3.13) |
LЕ = 10∙5,9/2 = 29,5 см
Рассчитывается коэффициент направленного действия антенны:
| (3.14) |
где n = 0,6 – КИП антенны
D = 4∙p∙152∙29,5∙0,5/4,52 = 1390
Рассчитывается диаграмма направленности антенны в плоскости Е, проходящей через фокальную линию:
| (3.15) |
где

Рис. 8. Диаграмма направленности антенны в плоскости Е
В плоскости Н, перпендикулярной фокальной линии, диаграмма направленности определяется по формуле:
| (3.16) |

Рис. 9. Диаграмма направленности антенны в плоскости Н
Рассчитывается коэффициент бегущей волны в питающем фидере:
| (3.17) |
где Г - коэффициент отражения, равный
Г = 3∙4,5/(4∙p∙49,8) = 0,021
КБВ = 0,959