Дискретные статистические ряды

Дискретный статистический ряд – это совокупность различных вариант 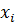и соответствующих им частот . Дискретный статистический ряд записывается в виде таблицы

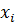
Характеристика положения

Выборочная средняя – это среднее арифметическое значение вариант статистического ряда. Вычисляется по формуле:

Мода – наиболее часто встречающаяся в ряду распреде­ления варианта, то есть варианта с наибольшей частотой..

Медиана – это серединная варианта, центральный член вариационного ряда. В статистике медиана приходится на тот член вариационного ряда, который «рассекает» совокупность на равные части. Если вариант в ряду четное количество, то медиана равна полусумме двух средних вариант.

Пример:

1. В распределении 12, 14, 16, 18, 20, 22, 24, 26, 28 медианой будет центральная варианта, , т.к. по обе стороны от нее отстоит по 4 варианты.

2. Для ряда с четным числом членов 6 8 10 12 14 16 18 20 медианой будет полусумма его центральных членов ).

Характеристика рассеяния

Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения.

или

Среднеквадратическое отклонение - корень квадратный из дисперсии:

Коэффициент вариации представляет процентное отношение среднеквадратического отклонения к среднему арифметическому.

Этот коэффициент позволяет оценивать вариабельность (разброс) признака в нормированных границах. Если его значение не превышает 10%, то можно говорить о сла­бом разбросе. Если коэффициент вариации находится в преде­лах 10–20%, разброс средний, если превышает 20%, то разброс вариант считают большим.

Вариационный размах равен разности между максимальным и минимальным значением показателя.

Задача 1. Дана выборка количества бракованных изделий продукции некоторого станка за последние 20 дней: . Требуется:

1) Составить вариационный и статистический ряды.

2) Построить полигон частот и кумулятивную кривую.

3) Найти эмпирическую функцию распределения.

4) Найти характеристики: среднее, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, вариационный размах.

Решение

1. Вариационный ряд: .

Статистический ряд:

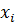
. Действительно, .

Найдем относительные и накопленные частоты. Результаты занесем в таблицу.

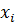
2. Полигон частот

Кумулята частот

3. Мода –

Медиана –

Выборочная средняя –

Выборочная дисперсия –

Среднее квадратическое отклонение –

Коэффициент вариации –

. Разброс большой.

Вариационный размах – .

Эмпирическая функция распределения

Эмпирической функцией распределения называется функция, определяемая следующим образом где – число вариант, меньших . Эмпирическая функция распределения служит хорошим приближением для неизвестной функции распределения при больших .

Эмпирическая функция распределения представляет собой разрывную ступенчатую функцию.

Найдем эмпирическую функцию распределения для приведенного выше примера:

;

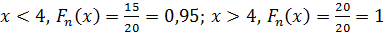Аналитически её можно записать следующим образом: