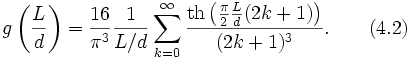Качественное объяснение эффекта

Содержание

 

Введение

Магниторезистивный эффект

Качественное объяснение эффекта

Тензор проводимости

Отрицательное магнетосопротивление

Вывод

Литература

Введение

 

В 2004 группа исследователей из Университета Айовы обнаружила необычный магнитный эффект, проявляемый пленками органических полупроводников. При приложении слабого магнитного поля к пленке ее электрическое сопротивление понижалось примерно на 10%. Эта необычная чувствительность к магнитным полям, известная как магниторезистивность, ранее проявлялась только для ферромагнитных материалов, как, например, железа. Причина наблюдаемого явления тогда, три года назад, не была выяснена.

 

 

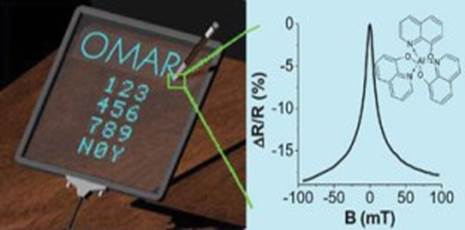
Сейчас исследователи сделали шаг вперед к пониманию проявления эффекта. Изучение пленок многочисленных органических полупроводников позволило определить, что уменьшение проводимости под действием магнитного поля происходит только при совместном присутствии в органических материалах тяжелых атомов переходных металлов (платина или иридий) и водорода.

На атомном уровне электрические и магнитные свойства атомов сильно связаны. Тяжелые атомы и водород совместно оказывают легкое влияние на энергетическое распределение электронов в пленке, в результате чего и проявляется магниторезистивность.

Маркус Вольгенаннт (Markus Wohlgenannt), возглавляющий исследование, отмечает, что результаты научных поисков уже сейчас могут быть использованы на практике, в органических светодиодных дисплеях, позволяющих сенсорный ввод информации с помощью магнитного стило.

Главное преимущество технологии, предлагаемой американскими исследователями в сравнении с существующими – понижение стоимости оборудования за счет изготовления дисплеев и магнитных ручек к ним из одного и того же материала.

 

Магниторезистивный эффект

 

Магниторезистивный эффект (магнетосопротивление) — изменение электрического сопротивления материала в магнитном поле. Впервые эффект был обнаружен в 1856 Уильямом Томсоном. В общем случае можно говорить о любом изменении тока через образец при том же приложенном напряжении и изменении магнитного поля. Все вещества в той или иной мере обладают магнетосопротивление. Для сверхпроводников, способных без сопротивления проводить электрический ток, существует критическое магнитное поле, которое разрушает этот эффект и вещество переходит в нормальное состояние, в котором наблюдается сопротивление. В нормальных металлах эффект магнетосопротивления выражен слабее. В полупроводниках относительное изменение сопротивления может быть в 100—10 000 раз больше, чем в металлах, и может достигать сотен тысяч процентов.

Магнетосопротивление вещества зависит и от ориентации образца относительно магнитного поля. Это связано с тем, что магнитное поле не изменяет проекцию скорости частиц на направление магнитного поля, но благодаря силе Лоренца закручивает траектории в плоскости перпендикулярной магнитному полю. Это объясняет, почему поперечное поле действует сильнее продольного. Здесь речь пойдёт в основном о поперечном магнетосопротивлении двумерных систем, когда магнитное поле ориентировано перпендикулярно к плоскости движения частиц.

На основе магниторезистивного эффекта создают датчики магнитного поля.

 

Качественное объяснение эффекта

 

Качественно понять это явление можно, если рассмотреть траектории положительно заряженных частиц (например, дырок) в магнитном поле. Пусть через образец проходит ток j вдоль оси X. Частицы обладают тепловой скоростью или если дырочный газ вырожден, то средняя скорость частиц равна фермиевской скорости (скорости частиц на уровне Ферми), которые должны быть много больше скорости их направленного движения (дрейфа). Без магнитного поля носители заряда движутся прямолинейно между двумя столкновениями.

Во внешнем магнитном поле B (перпендикулярного току) траектория будет представлять собой в неограниченном образце участок циклоиды длиной l (длина свободного пробега), и за время свободного пробега (время между двумя столкновениями) вдоль поля E частица пройдет путь меньший, чем l, а именно

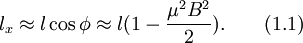
Поскольку за время свободного пробега τ частица проходит меньший путь вдоль поля E, то это равносильно уменьшению дрейфовой скорости, или подвижности, а тем самым и проводимости дырочного газа, то есть сопротивление должно возрастать. Разницу между сопротивлением при конечном магнитном поле и сопротивлением в отсутствие магнитного поля принято называть магнетосопротивлением.

Также удобно рассматривать не изменение полного сопротивления, а локальную характеристику проводника — удельное сопротивление в магнитном поле ρ(B) и без магнитного поля ρ (0). При учете статистического разброса времен (и длин) свободного пробега, получим

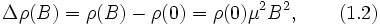
где μ — подвижность заряженных частиц, а магнитное поле предполагается малым 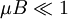. Это приводит к положительному магнетосопротивлению. В трёхмерных ограниченных образцах на боковых гранях возникает разность потенциалов, благодаря эффекту Холла в результате чего носители заряда движутся прямолинейно, поэтому магнетосопротивление с этой точки зрения должно отсутствовать. На самом деле оно имеет место и в этом случае, поскольку холлово поле компенсирует действие магнитного поля лишь в среднем, как если бы все носители заряда двигались с одной и той же (дрейфовой) скоростью. Однако скорости электронов могут быть различны, поэтому на частицы, движущиеся со скоростями, большими средней скорости, сильнее действует магнитное поле, чем холлово. Наоборот, более медленные частицы отклоняются под действием превалирующего холлова поля. В результате разброса частиц по скоростям уменьшается вклад в проводимость быстрых и медленных носителей заряда, что приводит к увеличению сопротивления, но в значительно меньшей степени, чем в неограниченном образце.

Тензор проводимости

 

Выражение (2.11) существенно упрощается если рассматривать двумерный дырочный газ (в плоскости XY) помещённый в поперечное магнитное поле. То есть магнитное поле направлено по оси Z

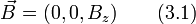
и магнитное поле и электрическое ортогональны между собой

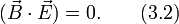
Тогда выражение (2.11) записанное в матричной форме примет вид

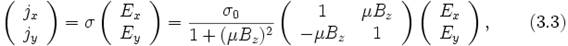
где тензор σ называют тензором проводимости двумерного дырочного газа в магнитном поле.

Если рассмотреть достаточно длинный образец прямоугольной формы, такой, что линии тока вдали от контактов параллельны боковым сторонам образца, то в этой системе отсутствует ток j_y. Можно записать связь между компонентами электрического поля (E_y называют холловским полем)

которая приводит к выражению для тока j_x

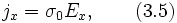
не зависящему от магнитного поля, то есть к отсутствию магнетосопротивления.

Обратная матрица к матрице проводимости называется тензором сопротивлений

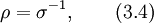
и в общем случае для обращения нужно использовать формулы

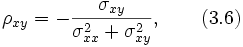
где вместо компонент тензора проводимости следует использовать компоненты в уравнении (3.3).

Для двумерного электронного газа используются формулы (3.3), где изменён знак на противоположный перед подвижностью в тензоре проводимости (или просто транспонированная матрица проводимости).

Геометрическое магнетосопротивление

 

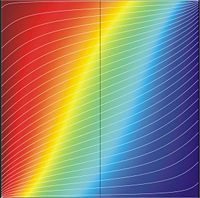
Рис. 1. Распределение потенциала (красный цвет соответствует максимуму, а синий — минимуму) в однородном квадратном образце с двумерным дырочным газом в поперечном магнитном поле (μB=1). Белыми линиями показаны искривлённые в магнитном поле линии тока.

 

Рис. 2. Распределение потенциала в однородном прямоугольном образце с двумерным дырочным газом в поперечном магнитном поле (μB=1). Белыми линиями показаны линии тока, которые в середине образца практически параллельны боковым сторонам.

 

Если рассмотреть прямоугольный образец (длиной L и шириной d) с двумерным электронным газом (магнитное поле направлено перпендикулярно плоскости образца), то в образце наблюдается магнитосопротивление связанное с перераспределением токов в магнитном поле:

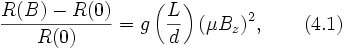
где