Лабораторная работа №11
ЦЕЛЬ РАБОТЫ: изучение затухающих электромагнитных колебаний в колебательном контуре и их характеристик.
ЛИТЕРАТУРА. 1. Телеснин Р.В., Яковлев В.Ф. Курс физики. Электричество. М.:”Просвещение”,1970, §§121,173-179. 2. Калашников С.Г. Электричество. М.: ”Наука”, 1977, §§89,91,99-102. 3. Савельев И.В. Курс общей физики. Кн.2. Электричество и магнетизм. М.:”Наука”, 1998, Гл.13.
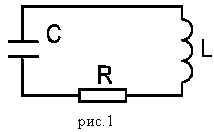КРАТКАЯ ТЕОРИЯ: Замкнутая цепь, состоящая из индуктивности и емкости, образует колебательный контур. Реальный колебательный контур обладает активным сопротивлением, характеризующим потери энергии в катушке индуктивности и соединительных проводах (рис.1).
Если зарядить конденсатор и замкнуть цепь, то в контуре возникнет электрический ток, мгновенное значение которого описывается законом Ома:
 ,
| (1) |
где: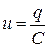 
- напряжение на обкладках конденсатора, 
- э.д.с. самоиндукции. Учитывая, что сила тока связана с изменением заряда конденсатора соотношением 
, получим:
| (2) |
Вводя подстановки:
 и 
| (3) |
Перепишем (2) в виде:
 ,
| (4) |
При условии 
решение уравнения (4) может быть записано в форме:
 ,
| (5) |
где:  ,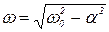
| (6) |
есть циклическая частота свободных колебания контура, a - коэффициент затухания, w о - циклическая частота собственных колебаний (при отсутствии затухания). За период затухающих колебаний принимают временной интервал между двумя ближайшими значениями u =0 и при этом 
имеют одинаковый знак.
График затухающих колебаний представлен на рисунке 2. Амплитуда напряжения изменяется со временем по экспоненциальному закону:
 ,
| (7) |
где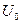 
- напряжение на конденсаторе при 
.Для характеристики колебаний служит логарифмический декремент затухания – натуральный логарифм отношения двух амплитуд (
и 
, рис. 2), отстоящих друг от друга по времени на один период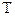 
:
 , 
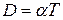
| (8) |
Из (6) следует, что при 
свободные колебания в контуре не возникают. В этом случае 
. Сопротивление 
называется критическим сопротивлением. Если 
³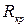 
, то разряд конденсатора носит апериодический характер (рис.3)
Для изучения электрических колебаний в данной работе используется осциллограф с малым временем послесвечения экрана. Колебания в контуре периодически возбуждаются короткими импульсами. Эпюры таких импульсов изображены на рисунке 4. Импульсы определенной амплитуды и длительности t овоспроизводятся периодически через время t (t -1- есть частота следования) генератором импульсов. Приборы типа Г5-I5 создают импульсы длительностью от 0,1 до10 мкс при частоте повторения порядка 
с-1.
ЭКСПЕРМЕНТАЛЬНАЯ ЧАСТЬ. Схема установки изображена на рис.5
На монтажной панели вмонтированы гнезда для включения конденсатора С, катушки индуктивности L, магазина резисторов Rм, генератора импульсов и осциллографа. Включая в контур различные L, С, изменяя сопротивление Rм, можно изучать влияние параметров контура на характеристики затухающих колебаний.
Элементы управления работой осциллографа (в дальнейшем – “ручки”) сгруппированы в блоки: “вход Y”,”синхронизация”, ”развертка”, ”калибровка”
Ручки “яркость”, “фокус” определяют качество линий изображения. Устойчивое изображение на экране достигается вращением “уровень” при положении переключателя синхронизации “внутр”. В этом случае колебания от различных импульсов (рис.4) “накладываются “ друг на друга.
Для измерения периода колебаний используется горизонтальная шкала сетки осциллографа. Расстоянию между двумя штрихами сетки (стороне клетки) соответствует определенное время – t0. Его значение (цена деления) определяется положением оцифрованной ручки “время/дел” (или “развертка”).
Перед измерениями следует проверка “нулевого” положение линии развертки сигнала. Для этого замыкают “вход Y” (переключатель – в положение “ ^ ”)исовмещают линию луча с осью Х сетки, вращением “ b ”. Далее переводят “вход Y” в режим работы с переменным напряжением: “~ ”.
Для вычисления периода колебаний Т определяют, скольким делениям N горизонтальной шкалы соответствует z полных колебаний:
.
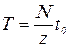Целесообразно “первый” переход напряжения через нуль совместить ручкой “« ” с ближайшей вертикальной линией сетки.
Декремент затухания вычисляют из отношения:
,
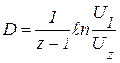где 
- амплитуда произвольного “первого” максимума, 
- амплитуда максимума с порядковым номером z. После проверки положения линии развертки можно нужный максимум ручкой “« ” совместить с осью Y сетки для и измерить амплитуду.
ЗАДАНИЕ.
1. Получить из (6) выражение для вычисления периода собственных колебаний контура (без затухания) 
по экспериментальным значениям Т и D для сравнения с 
на основе (3).
2. Ознакомиться с основными правилами пользования генератором импульсов и осциллографом.
3. Собрать схему согласно рис.5. Установить переключатели приборов в “начальные” положения, согласно приложению к установке.
4. Получить от преподавателя варианты комбинаций 
и 
для составления контуров. Записать их значения.
5. Для всех исследуемых контуров определить периоды колебаний и логарифмические декременты затухания. Вычислить периоды Т0Э, и Т0Т по формулам задания 1, a, и сопротивление контура R0= R.
6. Исследовать зависимость логарифмического декремента затухания от сопротивления контура (для одного из вариантов L,C). При расчете R следует к RМ прибавлять активное сопротивление катушки индуктивности (R0.). Значение R0 вычисляется в задании 5.
7. Пользуясь магазином резисторов, найти критическое сопротивление контура. Сравнить измеренное и рассчитанное значения.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какова цель данной работы?
2. Какими параметрами характеризуется затухающие колебания? Их физический смысл?
3. Какие приборы необходимы для выполнения задания?
4. Что понимают под периодом колебаний? Под периодом затухающих колебаний?
5. Какая зависимость изучаются экспериментально?
6. Какие величины определяются прямым методом?
7. Какие величины определяются косвенно?
8. Исходя из выражения (5), найти закон изменения силы тока в контуре.