Пример: используем ряд чисел из предыдущего примера.

Считаем, что сомнительным является значение, равное 126.

Вычисляем среднее арифметическое значение выборки без учета сомнительного значения измеряемой величины:

Ранее определили, что СКО равно 29,1. Тогда

, , 61,5 ≤ 87,3

Следовательно, сомнительное значение оставляем как равноправное в ряду наблюдений.

2. Критерий Романовского применяется, если число измерений n < 20.

При этом вычисляется отношение:

и сравнивается с критерием , выбранным по таблице.

Величины и вычисляют без учета экстремальных (вызывающих подозрение) значений .

Если то результат считается промахом и отбрасывается

Таблица - Значения критерия Романовского

q	n =4	n =6	n =8	n =10	n =12	n =15	n =20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Пример: На цементном заводе в процессе производства ежедневно в течение 45 дней брались пробы и определялось среднее сопротивление сжатию контрольных кубов (н/см² или кг/см²). Результаты наблюдения: 40, 33, 75, 18, 62, 33, 38, 69, 65, 100 (всего 10 измерений).

Считаем значение 18 – экстремальным и определяем среднее арифметическое без учета этого значения

Тогда СКО без учета экстремального значения

Отсюда

Сравнивается полученное значение с критерием , выбранным по таблице, приняв уровень значимости q = 0,01. Получим значение критерия Романовского, равное 2,62. Таким образом, получаем, что следовательно, результат = 18не считается промахом и не отбрасывается.

3. Критерий Шарлье - используется, если число наблюдений в ряду велико (n> 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину К_Шσ_x, будет n[1 - Ф(К_Ш)], где Ф(К_Ш) — значение нормированной функции Лапласа для X = К_Ш. Если сомнительным в ряду результатов наблюдений является один результат, то n[1-Ф(К_ш)] = 1. Отсюда Ф(К_Ш) = (n -1)/n.

Таблица – Значения критерия Шарлье

n
К_Ш	1,3	1,65	1,96	2,13	2,24	2,32	2,58

Пользуясь критерием Шарлье, отбрасывают результат, для значения которого в ряду из n наблюдений выполняется неравенство |х_i - х̅| > К_Шσ_.

Пример: используем ряд чисел, принятый при расчете критерия трех сигм.

Установлено, что СКО равно 29,1, среднее арифметическое – 64,5, а сомнительным определено значение – 126.

Тогда неравенство |х_i - х̅| > К_Шσ_. примет вид |126 – 64,5| < 29,1∙2,28, следовательно, сомнительный результат не отбрасывается, а остается в ряду чисел.

4. Критерий Диксона является достаточно универсальным в смысле числа наблюдений и применяется для выборки с небольшим количеством наблюдений. Практические вычисления проводят следующим образом:

1. Задаются критерием значимости q.

2. Ряд наблюдений записывают в вариационный ряд (например, возрастающий):

.

Сомнительным значением в данном случае должно быть значение с наибольшим порядковым номером, т.е. х_п.

3. Вычисляют критерий Диксона, который будет всегда положительным числом.:

4. Из таблицы находят критическое значение критерия Диксона Z_q (критическая область для критерия Диксона Р(К_Д > Z_q) = q).

Если 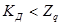сомнительное значение отбрасывают как промах.

Если сомнительное значение оставляют как равноправное в ряду наблюдений.

Таблица – Значения критерия Диксона

n	Z_q при q, равном
0,10	0,05	0,02	0,01
	0,68	0,76	0,85	0,89
	0,48	0,56	0,64	0,70
	0,40	0,47	0,54	0,59
	0,35	0,41	0,48	0,53
	0,29	0,35	0,41	0,45
	0,28	0,33	0,39	0,43
	0,26	0,31	0,37	0,41
	0,26	0,30	0,36	0,39
	0,22	0,26	0,31	0,34

Пример: используем ряд чисел из предыдущего примера.

Поиск по сайту