Лекция №7
Погрешности измерений. Доверительная вероятность и доверительный интервал. Грубые погрешности и методы их исключения.
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности, а сам интервал - доверительным интервалом.
Каждой доверительной вероятности соответствует свой доверительный интервал. В частности, доверительной вероятности 0,67 соответствует доверительный интервал от  до
до  . Однако это утверждение справедливо только при достаточно большом числе измерений (более 10), да и вероятность 0,67 не представляется достаточно надежной - примерно в каждой из трех серий измерений y может оказаться за пределами доверительного интервала. Для получения большей уверенности в том, что значение измеряемой величины лежат внутри доверительного интервала, обычно задаются доверительной вероятностью 0,95 - 0,99. Доверительный интервал для заданной доверительной вероятности
. Однако это утверждение справедливо только при достаточно большом числе измерений (более 10), да и вероятность 0,67 не представляется достаточно надежной - примерно в каждой из трех серий измерений y может оказаться за пределами доверительного интервала. Для получения большей уверенности в том, что значение измеряемой величины лежат внутри доверительного интервала, обычно задаются доверительной вероятностью 0,95 - 0,99. Доверительный интервал для заданной доверительной вероятности  с учетом влияния числа измерений n можно найти, умножив стандартное отклонение среднего арифметического
с учетом влияния числа измерений n можно найти, умножив стандартное отклонение среднего арифметического
 .
.
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента  для ряда значений
для ряда значений  и n приведены в таблице.
и n приведены в таблице.
Таблица - Коэффициенты Стьюдента 
| Число измерений n | Доверительная вероятность y | |||
| 0,67 | 0,90 | 0,95 | 0,99 | |
| 2,0 | 6,3 | 12,7 | 63,7 | |
| 1,3 | 2,4 | 3,2 | 5,8 | |
| 1,2 | 2,1 | 2,8 | 4,6 | |
| 1,2 | 2,0 | 2,6 | 4,0 | |
| 1,1 | 1,8 | 2,3 | 3,3 | |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие

Величину  мы будем называть случайной погрешностью величины y.
мы будем называть случайной погрешностью величины y.
Пример: см. лекцию №5 – ряд чисел.
Определим

При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Промахи(грубая погрешность) - грубые погрешности, связанные с ошибками оператора или неучтенными внешними воздействиями. Их обычно исключают из результатов измерений. Промахи, как правило, вызываются невнимательностью. Они могут возникать также вследствие неисправности прибора.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
- неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
- неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
- хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Методы обнаружения и исключения грубых погрешностей
Проверяемая гипотеза состоит в утверждении, что результат наблюдения  не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.
не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.
Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительномог иметь место в данной совокупности результатов измерений.Обычно проверяют наибольшее и наименьшее з начения результатовизмерений. Для проверки гипотез используются следующие критерии:
1. Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. Данный критерий надежен при числе измерений n > 20... 50.
По этому критерию считается, что результат маловероятен и его можно считать промахом, если:
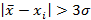
где  – среднее арифметическое отдельных результатов измерений:
– среднее арифметическое отдельных результатов измерений:

где n – число измерений;
 – результат i -го измерения;
– результат i -го измерения;
 – среднее квадратичное отклонение (СКО):
– среднее квадратичное отклонение (СКО):

Величины  и
и  вычисляют без учета экстремальных (вызывающих подозрение) значений
вычисляют без учета экстремальных (вызывающих подозрение) значений 
Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее либо наименьшее значение наблюдения измеряемой величины.
Вычисляют среднее арифметическое значение выборки без учета сомнительного значения измеряемой величины:

Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают с СКО.
Если  , то сомнительное значение отбрасывают, как промах.
, то сомнительное значение отбрасывают, как промах.
Если  , то сомнительное значение оставляют как равноправное в ряду наблюдений.
, то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов является самым популярным, достаточно надежным и удобным, так как при этом ни каких таблиц под рукой иметь нет необходимости.