1. 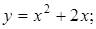
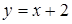 . 2.
. 2. 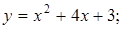
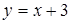 .
.
3. 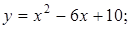
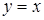 . 4.
. 4. 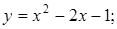
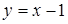 .
.
5. 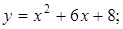
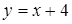 . 6.
. 6. 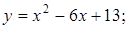
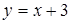 .
.
7. 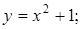
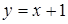 . 8.
. 8. 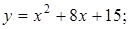
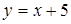 .
.
9. 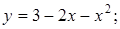
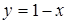 . 10.
. 10. 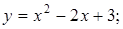
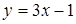 .
.
11. 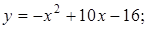
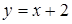 . 12.
. 12. 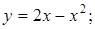
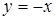 .
.
13. 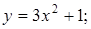
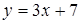 . 14.
. 14. 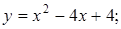
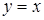 .
.
15. 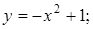
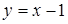 . 16.
. 16. 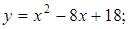
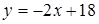 .
.
17. 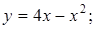
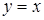 . 18.
. 18. 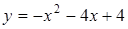 ;
; 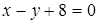 .
.
19. 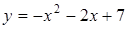 ;
; 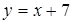 . 20.
. 20. 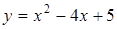 ;
; 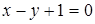 .
.
5. По методу наименьших квадратов найти прямую 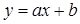 , которая наилучшим образом согласуется с опытными данными:
, которая наилучшим образом согласуется с опытными данными:
1. 2.
| x | x | –1 | ||||||||
| y | 4,1 | 2,8 | 2,1 | 1,0 | y | 3,9 | 3,2 | 1,9 | 1,0 |
3. 4.
| x | –3 | –2 | –1 | x | –2 | –1 | ||||
| y | 0,7 | 4,5 | 6,9 | 9,9 | y | 1,1 | 3,9 | 6,9 | 10,1 |
5. 6.
| x | x | |||||||||
| y | 0,9 | 4,1 | 7,1 | 9,9 | y | 1,3 | 3,5 | 7,1 | 10,1 |
7. 8.
| x | –1 | –2 | –3 | –4 | x | |||||
| y | 0,8 | 4,3 | 7,0 | 9,9 | y | 1,2 | 3,7 | 7,0 | 10,1 |
9. 10.
| x | x | –4 | –3 | –2 | –1 | |||||
| y | 0,9 | 4,2 | 6,9 | 10,0 | y | 1,1 | 3,8 | 7,1 | 10,0 |
11. 12.
| x | x | –1 | ||||||||
| y | 6,7 | 5,5 | 2,9 | 0,9 | y | 7,1 | 4,9 | 2,9 | 1,1 |
13. 14.
| x | x | –2 | –1 | |||||||
| y | 6,9 | 5,1 | 3,1 | 0,9 | y | 7,3 | 4,5 | 3,1 | 1,1 |
15. 16.
| x | -4 | -3 | -2 | -1 | x | |||||
| y | 6,8 | 5,3 | 3,0 | 0,9 | y | 7,2 | 4,7 | 3,0 | 1,1 |
17. 18.
| x | x | -3 | -2 | -1 | ||||||
| y | 1,1 | 2,8 | 5,1 | 9,0 | y | 7,1 | 4,8 | 3,1 | 1,0 |
19. 20.
| x | -2 | -1 | x | |||||||
| y | 0,9 | 3,2 | 4,9 | 9,0 | y | 1,2 | 2,7 | 9,1 |
6. Решить задачи:
1. В классе 19 мальчиков и 11 девочек. По списку выбирают двух дежурных. Какова вероятность того, что ими окажутся:
1. два мальчика;
2. девочка и мальчик;
3. хотя бы один мальчик.
2. Имеются 10 билетов в театр, из которых четыре на места первого ряда. Выбирают два билета. Какова вероятность того, что:
1. на первый ряд билетов не окажется;
2. достанется только один билет на первый ряд;
3. хотя бы один билет будет на первый ряд.
3. В ящике находятся 12 деталей, из них 8 стандартных. Рабочий берет одну за другой две детали. Найти вероятность того, что:
1. обе детали окажутся стандартными;
2. только одна деталь стандартная;
3. хотя бы одна деталь окажется стандартной.
4. Из пятидесяти дискет, имеющихся в продаже, четыре имеют скрытый дефект. Какова вероятность того, что две купленные дискеты:
1. качественные;
2. только одна с дефектом;
3. хотя бы одна дефектная.
5. Из букв слова “УРАВНЕНИЕ” наугад выбирают две буквы. Какова вероятность того, что:
1. эти буквы гласные;
2. одна гласная, а другая согласная;
3. обе буквы согласные.
6. В колоде 36 карт. Выбирают две карты. Какова вероятность того, что ими окажутся:
1. тузы;
2. хотя бы одна карта туз;
3. ни одного туза.
7. Из 11 машин на станции технического обслуживания 4 имеют неисправности в моторе, а другие имеют неисправности в ходовой части. Какова вероятность, что из первых двух машин взятых на ремонт:
1. обе имеют неисправности в моторе;
2. одна машина имеет неисправность в моторе;
3. хотя бы одна машина имеет неисправность в моторе.
8. В ящике 7 черных шаров и 13 белых. Вынимают два шара. Найти вероятность того, что:
1. оба шара черные;
2. оба шара разных цветов;
3. оба белые.
9. В лотерее разыгрывается 100 билетов, из которых 5 выигрышных. Некто покупает два билета. Найти вероятность того, что эти билеты окажутся:
1. без выигрыша;
2. хотя бы один билет выиграет;
3. только один выиграет.
10. В коробке находится 6 новых и 2 израсходованные батарейки от карманного фонарика. Какова вероятность того, что две вынутые на удачу батарейки окажутся:
1. новыми;
2. только одна новая;
3. ни одной новой.
11. На тепловой станции 15 сменных инженеров, из них 5 женщин. В смену занято два инженера. Найти вероятность того, что:
1. ими окажутся женщины;
2. хотя бы одна женщина;
3. только одна женщина.
12. В стаде 40 коров, из которых 26 имеют среднесуточный удой более 10кг. Выбирают двух животных. Какова вероятность, что:
1. обе коровы имеют удой более 10кг;
2. только одна корова имеет удой более 10кг;
3. ни одной с удоем более 10кг.
13. В коробке 8 карандашей, из них 3 сломанных. Какова вероятность, что среди двух вынутых карандашей:
1. два сломанных;
2. хотя бы один сломанный;
3. только один сломанный.
14. Первый рабочий за смену изготовил 120 изделий, а второй 140. Какова вероятность, что две детали, взятые со склада, изготовил:
1. первый рабочий;
2. второй рабочий;
3. только одна деталь изготовлена первым рабочим.
15. В первом ящике 10 шаров, из них 3 черных и 7 белых, во втором ящике 12 шаров, из них 4 черных и 8 белых. Из каждого ящика наугад вынимают по одному шару. Найти вероятность того, что эти шары:
1. будут черными;
2. только один черный;
3. хотя бы один черный.
16. В корзине 12 плодов, из низ 3 заражены болезнью в скрытой форме. Из корзины последовательно извлекаются 2 плода. Вычислить вероятность того, что:
1. они оба окажутся больными;
2. только один здоровый плод;
3. хотя бы один здоровый плод.
17. В группе из 30 учеников на контрольной работе 6 учеников получили оценку “отлично”, 10 учеников – “хорошо”, 9 учеников – “удовлетворительно”. Вычислить вероятность того, что два ученика вызванные к доске:
1. имеют неудовлетворительные оценки по контрольной работе;
2. хотя бы один имеет отличную оценку;
3. оба имеют удовлетворительную оценку.
18. В списке жильцов 52 фамилии, причем 37 из них начинаются с согласной буквы. Какова вероятность того, что из двух выбранных наудачу человек:
1. оба имеют фамилию, которая начинается с согласной буквы;
2. только один имеет фамилию, которая начинается с гласной буквы;
3. хотя бы один имеет фамилию, которая начинается с гласной буквы.
19. В партии семян, состоящей из 10 мешков, 4 мешка с нестандартными семенами. На проверку отбирают два мешка. Какова вероятность того, что:
1. эти мешки с нестандартными семенами;
2. только один мешок с нестандартными семенами;
3. оба мешка с семенами, удовлетворяющими стандарту.
20. В лесовоз загрузили 50 бревен хвойных пород и 10 бревен лиственных пород. При разгрузке, при открывании бортов, выпадают два бревна. Какова вероятность того, что:
1. оба выпавшие бревна хвойных пород;
2. хотя бы одно бревно хвойной породы;
3. только одно выпавшее бревно хвойной породы.
7. В задачах 361-380 задан закон распределения случайной величины 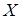 (в первой строке таблицы даны возможные значения величины
(в первой строке таблицы даны возможные значения величины 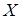 , а во второй строке указаны вероятности
, а во второй строке указаны вероятности 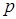 этих возможных значений).
этих возможных значений).
Найти: 1) Математическое ожидание  ;
;
2) Дисперсию 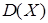 ;
;
3) Среднее квадратическое отклонение 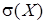
1. 2.
| Х | –6 | Х | –2 | |||||||
| р | 0,1 | 0,1 | 0,6 | 0,2 | р | 0,5 | 0,1 | 0,2 | 0,2 |
3. 4.
| Х | –2 | –1 | Х | –1 | ||||||
| р | 0,2 | 0,5 | 0,1 | 0,2 | р | 0,4 | 0,4 | 0,1 | 0,1 |
5. 6.
| Х | –5 | –4 | –2 | Х | –1 | |||||
| р | 0,1 | 0,5 | 0,2 | 0,2 | р | 0,2 | 0,5 | 0,1 | 0,2 |
7. 8.
| Х | –6 | –3 | Х | –8 | –6 | –1 | ||||
| р | 0,3 | 0,3 | 0,2 | 0,2 | р | 0,5 | 0,1 | 0,3 | 0,1 |
9. 10.
| Х | –4 | –2 | Х | –2 | ||||||
| р | 0,1 | 0,3 | 0,2 | 0,4 | р | 0,1 | 0,1 | 0,3 | 0,5 |
11. 12.
| Х | –7 | –2 | Х | –4 | –1 | |||||
| р | 0,1 | 0,3 | 0,2 | 0,4 | р | 0,1 | 0,6 | 0,2 | 0,1 |
13. 14.
| Х | –5 | –2 | Х | –3 | –1 | |||||
| р | 0,1 | 0,3 | 0,2 | 0,4 | р | 0,3 | 0,2 | 0,3 | 0,2 |
15. 16.
| Х | Х | –3 | ||||||||
| р | 0,1 | 0,2 | 0,2 | 0,5 | р | 0,1 | 0,6 | 0,2 | 0,1 |
17. 18.
| Х | –5 | Х | –3 | |||||||
| р | 0,2 | 0,3 | 0,1 | 0,4 | р | 0,1 | 0,7 | 0,1 | 0,1 |
19. 20.
| Х | Х | –3 | –1 | |||||||
| р | 0,4 | 0,3 | 0,2 | 0,1 | р | 0,2 | 0,1 | 0,2 | 0,5 |