Лекция №9
Обработка результатов измерений
Проверка нормальности распределения результатов наблюдений группы.
1. При числе результатов наблюдений n <50 нормальность их распределения проверяют при помощи составного критерия.
Критерий 1. Вычисляют отношение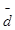 
,
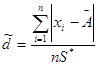где S* - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле
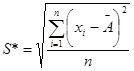
Результаты наблюдений группы можно считать распределенными нормально, если
,
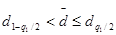где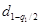 
и 
- квантили распределения, получаемые из таблицы по n, q 1/2 и (1 – q 1/2), причем q 1 - заранее выбранный уровень значимости критерия.
Таблица 1 - Статистика d
| n | q 1/2 100% | (1- q 1/2) 100% | ||
| 1 % | 5 % | 95 % | 99 % | |
| 0,9137 | 0,8884 | 0,7236 | 0,6829 | |
| 0,9001 | 0,8768 | 0,7304 | 0,6950 | |
| 0,8901 | 0,8686 | 0,7360 | 0,7040 | |
| 0,8826 | 0,8625 | 0,7404 | 0,7110 | |
| 0,8769 | 0,8578 | 0,7440 | 0,7167 | |
| 0,8722 | 0,8540 | 0,7470 | 0,7216 | |
| 0,8682 | 0,8508 | 0,7496 | 0,7256 | |
| 0,8648 | 0,8481 | 0,7518 | 0,7291 |
Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей 
превзошли значение zp/2 S, где S - оценка среднего квадратического отклонения, вычисляемая по формуле
,
где zp/2 - верхний квантиль распределения нормированной функции Лапласа, отвечающий вероятности Р/2.
Значения Р определяются из таблицы по выбранному уровню значимости q2 и числу результатов наблюдений n.
При уровне значимости, отличном от предусмотренных в таблице, значение Р находят путем линейной интерполяции.
В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q 1, а для критерия 2 - q 2, то результирующий уровень значимости составного критерия
q ≤ q 1 + q 2.
В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.
Таблица - Значения Р для вычисления
| n | m | q2· 100 % | ||
| 1 % | 2 % | 5 % | ||
| 0,98 | 0,98 | 0,96 | ||
| 11-14 | 0,99 | 0,98 | 0,97 | |
| 15-20 | 0,99 | 0,99 | 0,98 | |
| 21-22 | 0,98 | 0,97 | 0,96 | |
| 0,98 | 0,98 | 0,96 | ||
| 24-27 | 0,98 | 0,98 | 0,97 | |
| 28-32 | 0,99 | 0,98 | 0,97 | |
| 33-35 | 0,99 | 0,98 | 0,98 | |
| 36-49 | 0,99 | 0,99 | 0,98 |
2. Доверительные границы ε (без учета знака) случайной погрешности результата измерения находят по формуле
,
где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по таблице.
Таблица - Значение коэффициента t для случайной величины Y, имеющей распределение Стьюдента с n-1 степенями свободы
| n -1 | Р =0,95 | Р =0,99 | n -1 | Р =0,95 | Р =0,99 |
| 3,182 | 5,841 | 2,120 | 2,921 | ||
| 2,776 | 4,604 | 2,101 | 2,878 | ||
| 2,571 | 4,032 | 2,086 | 2,845 | ||
| 2,447 | 3,707 | 2,074 | 2,819 | ||
| 2,365 | 3,499 | 2,064 | 2,797 | ||
| 2,306 | 3,355 | 2,056 | 2,779 | ||
| 2,262 | 3,250 | 2,048 | 2,763 | ||
| 2,228 | 3,169 | 2,043 | 2,750 | ||
| 2,179 | 3,055 | ∞ | 1,960 | 2,576 | |
| 2,145 | 2,977 |
9.1.1. Форма записи результатов измерений:
1. При симметричной доверительной погрешности результаты измерений представляют в форме
,
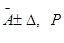где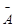 
- результат измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.
2. При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей результаты измерений представляют в форме
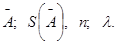
Суммирование погрешностей. Округление и представление результата.
Суммирование погрешностей. В теории вероятностей показывается, что в тех случаях, когда погрешности вызываются несколькими независимыми друг от друга случайными причинами, то складываются не сами погрешности, а их квадраты. Поэтому полная абсолютная погрешность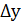 
измеряемой величины через ее случайную 
и приборную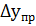 
погрешности выражается формулой
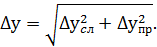
Здесь предполагается, что погрешностям и 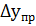соответствуют приблизительно одинаковые доверительные вероятности. Такую же доверительную вероятность будет иметь и .
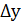Из формулы следует, что в случае, когда одна из погрешностей или 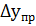даже в небольшое число раз меньше другой, то ее вклад в полнуюпогрешность оказывается незначительным.
Относительная погрешность. Кроме абсолютной погрешности результат также характеризуется еще и относительной погрешностью, т.е. отношением 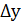к среднему арифметическому значению 
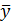. Относительная погрешность 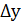/ 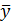выражается в виде десятичной дроби или в процентах и показывает качество измерения. Если при измерениях получена относительная погрешность более 10%, то говорят, что произведено не измерение, а лишь оценка измеряемой величины. В лабораториях физического практикума относительная погрешность обычно составляет 1-10%.
Округление результата и погрешности начинают с абсолютной погрешности!!!
Число значащих цифр, которое оставляют в значении погрешности, вообще говоря, зависит от коэффициента надежности и числа измерений. Однако даже для очень точных измерений (например, астрономических), в которых точное значение погрешности важно, не оставляют более двух значащих цифр. Большее число цифр не имеет смысла, так как определение погрешности само имеет свою погрешность.
Чаще всего на практике сравнительно небольшой коэффициент надежности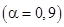 
и малое число измерений. Поэтому при округлении (с избытком) полной абсолютной погрешности оставляют одну значащую цифру.
Разряд значащей цифры абсолютной погрешности определяет разряд первой сомнительной цифры взначении результата. Следовательно, само значение результата нужно округлять (с поправкой) до той значащей цифры, разряд которой совпадает с разрядом значащей цифры погрешности. Сформулированное правило следует применять и в тех случаях, когда некоторые из цифр являются нулями.
Пример. Если при измерении массы тела получен результат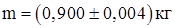 
, то писать нули в конце числа 0,900 необходимо. Запись 
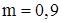означала бы, что о следующих значащих цифрах ничего неизвестно, в то время как измерения показали, что они равны нулю.
Результаты измерений и погрешности следует округлять по сложившимсяправилам:
1. Округление проводится только один раз при получении окончательных результатов. Все промежуточные результаты целесообразно представлять тем числом разрядов, которые удается получить.
2. Округление начинается с округления погрешности результата измерения.
3. Погрешность результата измерения округлятся до двух значащих цифр, если при движении слева направо первая значащая цифра округляемой погрешности меньше 3. Погрешность результата измерения округляется до одной значащей цифры, если при движении слева направо первая значащая цифра округляемой погрешности больше 3 или равна 3.
4. Результат измерения округляется так, чтобы он оканчивался цифрой того же разряда, что и значение погрешности. Если числовое значение результата измерения представляется десятичной дробью, оканчивающейся нулями, то нули отбрасываются только до того разряда, который соответствует разряду числового значения погрешности.
5. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры в числе не изменяют. Если эта цифра больше 5, то последнюю оставляемую цифру увеличивают на единицу. Лишние цифры в целых числах заменяют нулями, а в десятичных дробях отбрасывают.
Например, результат измерения U = 25,4587 мВ при погрешности результата Δ = ±0,0213 мВ. Округление начинается с погрешности. После округления погрешность Δ = ±0,021 мВ и результат измерения U = 25,459 мВ. Результат измерения с учетом погрешности запишется в виде U' = (25,459±0,021) мВ. Если погрешность (при том же результате измерения) Δ = ±6,25 мВ, то после округления Δ = ±6 мВ, U = 25 мВ и результат измерения с учетом погрешности U' = (25±6) мВ.
6. Если отбрасываемая цифра равна 5, а следующие за ней цифры отсутствуют или нули, то последнюю сохраняемую цифру числа не изменяют.
Если отбрасываемая цифра равна 5, а следующие за ней цифры отличны от нуля, то последнюю сохраняемую цифру числа увеличивают на единицу.
7. Примеры округления:
а) результат измерения А = 625,47; погрешность ΔА = ±7,24. После округления: ΔА = ±7; А = 625 и результат измерения с учетом погрешности А' = (625±7);
б) результат измерения В = 1055,53; погрешность ΔВ = ±5,29. После округления: ΔВ = ±5; В = 1056 и результат измерения с учетом погрешности В' = (1056±5);