Понятие корреляции
Рассмотрим два показателя Х и Y. Предположим, что они зависимы, то есть изменение одного из них влечет за собой изменение другого.
Функциональная связь – связь, при которой, каждому значению одного показателя соответствует одно значение другого показателя.
Однако на практике чаще встречаются связи иного вида.
Корреляционная связь (статистическая, стохастическая или вероятностная) - связь, при которой каждому значению одного показателя соответствует несколько значений другого показателя. При этом, зная значение Х, нельзя точно определить Y, так как на Y кроме Х влияет еще множество неучтенных факторов. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, стоимость одного экземпляра книги от тиража, выработки рабочего за смену от его квалификации и т.д.
Виды корреляционной связи.
По направлению связи:
Положительная (прямая) – с увеличением (уменьшением) одного признака в основном увеличивается (уменьшается) значения другого.
Отрицательная (обратная) – с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого.
Относительно своей аналитической формы:
Линейная – между признаками в среднем проявляются линейные соотношения.
Нелинейная – выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
С точки зрения взаимодействующих факторов.
Парная – характеризуется связь 2 признаков.
Множественная – изучаются более чем 2 переменные.
Также подразделяется на сильную и слабую.
Характер корреляционной зависимости изучается в регрессионном анализе, а сила корреляционной связи – в корреляционном анализе (от лат. сorrelation - взаимоотношение, взаимодействие).
Методы выявления наличия корреляционной связи
Изучение корреляционных зависимостей производится табличным, графическим и аналитическим способом.
1. При табличном изучении корреляционных связей зависимость между показателями Х и Y задается двумерной таблицей, называемой корреляционной решеткой.
2. При графическом способе на координатную плоскость наносятся точки, расположение которых соответствует значениям показателей Х и Y.
Возможны случаи:

Если точки на графике расположены равномерно в виде окружности или овала и разброс точек велик (а), то корреляция между признаками отсутствует.
Если корреляционное поле имеет вид эллипса со сгущением точек вокруг его продольной оси, то между признаками имеется связь. По тому, как располагается условная диагональ – ось сгущения, можно судить о знаке корреляции. На рис. в) Положительная корреляция, а на г) отрицательная. Если точки располагаются вдоль прямой, то это отражает наличие функциональной связи.
Расположение точек в корреляционной решетке не всегда бывает таким правильным. Нахождение одной или нескольких точек в стороне от основного массива может резко изменить предполагаемое значение коэффициента корреляции. Поэтому для более точного определения степени связи необходим аналитический метод.
3. Аналитический метод основан на расчете коэффициента корреляции.
Коэффициент парной корреляции Пирсона  .
.
Он вычисляется для выборок, распределенных по закону, близкому к нормальному. Для расчета используют формулу:
 =
=  ,
,
где
 =
=  (x1+x2+…+xn),
(x1+x2+…+xn),  =
=  (y 1 +y 2 +…+yn),
(y 1 +y 2 +…+yn),
 =
=  (x 12 +x 22 +…+xn 2 ),
(x 12 +x 22 +…+xn 2 ), 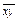 =
=  (x 1 y 1 +x 2 y 2 +…+xnyn).
(x 1 y 1 +x 2 y 2 +…+xnyn).
 =
=  (y 12 +y 22 +…+yn 2).
(y 12 +y 22 +…+yn 2).
Коэффициент ранговой корреляции Спирмена  .
.
Используется если условие нормальности распределения выборочных данных не выполняется. Ранговую корреляцию используют также в ситуации, когда показатели нельзя измерить численно, но можно проранжировать, расположив по возрастанию качества. Кроме того, корреляцию Спирмена часто используют в случае, когда объемы выборок велики, т.к. в вычислительном плане расчет коэффициента Спирмена намного менее трудоемок, чем Пирсона.
Для его вычисления каждому элементу  выборки показателя Х присваивается ранг – порядковый номер этого элемента в вариационном ряду (выборке, записанной по возрастанию значений элементов). Если несколько соседних элементов вариационного ряда равны по величине, то их ранг равен среднеарифметическому их порядковых номеров.
выборки показателя Х присваивается ранг – порядковый номер этого элемента в вариационном ряду (выборке, записанной по возрастанию значений элементов). Если несколько соседних элементов вариационного ряда равны по величине, то их ранг равен среднеарифметическому их порядковых номеров.
Пусть  - ранг элемента
- ранг элемента  ,
,
 - ранги элементов
- ранги элементов  второй выборки показателя Y. Тогда, коэффициент корреляции Спирмена вычисляется по формуле:
второй выборки показателя Y. Тогда, коэффициент корреляции Спирмена вычисляется по формуле:
rs =  .
.
Коэффициент корреляции r (как Пирсона, так и Спирмена) обладает следующими свойствами:
1. Коэффициент корреляции изменяется в пределах  .
.
2. Модуль коэффициента корреляции характеризует силу статистической связи, чем больше  , тем сильнее связь, в частности если
, тем сильнее связь, в частности если  , то связь функциональная, если r близок к нулю, то связь слабая или отсутствует.
, то связь функциональная, если r близок к нулю, то связь слабая или отсутствует.
 - очень слабая;
- очень слабая;  - слабая;
- слабая;  - средняя;
- средняя;
 - сильная;
- сильная;  - очень сильная.
- очень сильная.
3. Знак коэффициента корреляции характеризует направление статистической связи, если  , то с ростом Х показатель Y также растет, если
, то с ростом Х показатель Y также растет, если  , то с ростом Х показатель Y убывает.
, то с ростом Х показатель Y убывает.
4. Величина  называется коэффициентом детерминации, его можно интерпретировать как среднюю долю влияния показателя Х на Y.
называется коэффициентом детерминации, его можно интерпретировать как среднюю долю влияния показателя Х на Y.
Задача. Изучается зависимость продаж товара у (млн.руб.) от затрат на рекламу этого товара х (тыс.руб.).Для решения этой задачи были получены данные наблюдений, приведенные в таблице. Необходимо:
1) Найти коэффициент парной корреляции Пирсона.
2) Найти коэффициент ранговой корреляции Спирмена.
| Значения фактора xi | ||||||||||
| Значения фактора yi |
Решение
1) Находим коэффициент парной корреляции Пирсона:
 =
=  (37+48+39+19+28+33+24+43+41+32) = 34,4;
(37+48+39+19+28+33+24+43+41+32) = 34,4;
 =
=  (32+39+27+21+21+36+26+34+30+34) = 30;
(32+39+27+21+21+36+26+34+30+34) = 30;
 =
=  (372+482+392+192+282+332+242+432+412+322) = 1255,8;
(372+482+392+192+282+332+242+432+412+322) = 1255,8;
 =
=  (322+392+272+212+212+362+262+342+302+342) = 934;
(322+392+272+212+212+362+262+342+302+342) = 934;
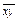 =
=  (37
(37  +48
+48  +39
+39  +19
+19  +28
+28  +33
+33  +24
+24  +43
+43  + +41
+ +41  +32
+32  ) = 1068,8;
) = 1068,8;
rxy =  = 0,742.
= 0,742.
Значит, связь положительная и сильная.
2) Находим коэффициент ранговой корреляции Спирмена. Для этого вычисляем ранги элементов обоих выборок:
| Значение фактора xi | ||||||||||
Ранг фактора 
| ||||||||||
| Значение фактора yi | ||||||||||
Ранг фактора 
| 1,5 | 1,5 | 7,5 | 7,5 |
По формуле (4) вычисляем коэффициент корреляции:
 = 0+0+32+0,52+1,52+42+12+1,52+32+3,52 = 52;
= 0+0+32+0,52+1,52+42+12+1,52+32+3,52 = 52;
rs =  = 0,685.
= 0,685.
Коэффициент корреляции Спирмена также достаточно высок, что подтверждаем предположение о том, что между данными показателями существует достаточно сильная положительная зависимость.
Уравнение регрессии. Коэффициент регрессии
Регрессионный анализ выражает зависимость между переменными величинами как зависимость между аргументом x и функцией y. Задача регрессионного анализа состоит в нахождении зависимости вида  .
.