Круговая диаграмма неразветвленной цепи.

Теоретическая часть

Для расчета синусоидальных величин (токов, напряжений, ЭДС), т.е. для выполнения алгебраических операций над ними, переходят в комплексную расчетную область. Сущность метода состоит в том, что синусоидальные токи, напряжения, ЭДС изображаются комплексными числами, что позволяет рассчитывать цепи синусоидального тока с использованием алгебраических уравнений аналогично цепям постоянного тока. Комплексные числа , , 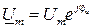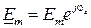называют комплексными амплитудами соответственно синусоидального тока, напряжения и ЭДС, а комплексные числа 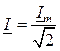, , 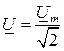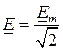– комплексными действующими значениями тока, напряжения и ЭДС. Введенные комплексы 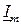, , 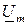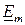(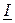, , 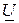) однозначно описывают переменные 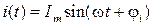, , 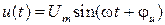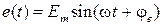(существует взаимно-однозначное соответствие). Каждому комплексу 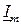, , 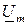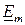(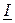, , 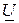) соответствует мгновенное значение соответственно синусоидального тока, напряжения и ЭДС: амплитуда равна длине (модулю) комплексной амплитуды, которая в раз больше длины (модуля) комплекса действующего значения, а начальная фазы равна углу комплексной амплитуды и комплекса действующего значения. Введение вместо синусоидальных функций времени i (t), u (t), e (t) комплексов 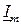, , 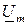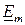(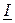, , 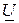) позволяет записать компонентные уравнения элементов цепи в комплексной форме (таблица 5.1).

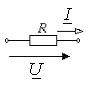
Компонентные уравнения резистивного, емкостного и индуктивного элементов в комплексной области описываются алгебраическим уравнением:

,

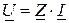где 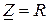для резистивного элемента, 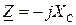– для емкостного элемента, 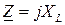– для индуктивного элемента. Уравнение представляет собой запись закона Ома в комплексной форме для резистивного, емкостного и индуктивного элементов.

Таблица 5.1

Элемент	Временная область	Комплексная область
изображение	уравнение	изображение	уравнение
резистивный
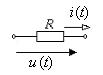
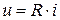
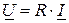
емкостной
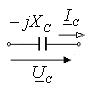
индуктивный
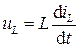
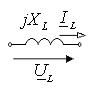
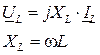
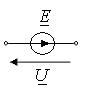
источник ЭДС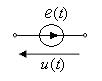
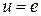
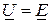
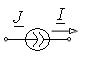
источник тока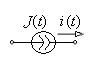

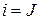
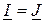
Для расчета составляют комплексную схему замещения цепи и математическое описание всех ее элементов в комплексной области. Используя уравнения Кирхгофа в комплексной форме 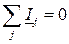и 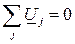(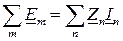), можно получить полное математическое описание цепи в комплексной форме. Цепь в этой области описывается чисто алгебраическими уравнениями. Решив эти уравнения, т.е. определив комплексы всех токов и напряжений цепи, от последних переходят к мгновенным значениям (соответствующим синусоидальным функциям токов и напряжений). Представление синусоидальных токов, напряжений и ЭДС комплексными числами позволяет изображать их на комплексной плоскости в виде векторов, отображая действия, производимые над этими числами в процессе расчета цепей, в виде построений соответствующих векторных диаграмм. Удобной иллюстрацией расчета является векторная диаграмма токов (ВДТ) и топографическая диаграмма напряжений (ТДН), отражающая соотношения между комплексами токов и напряжений на любом участке цепи и позволяющая находить графическим путем напряжение между любыми точками электрической цепи без дополнительного расчета.

Для участка цепи с комплексным напряжением 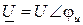и комплексным током вводят понятие комплексной мощности: 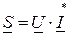, где 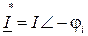комплексно-сопряженный вектор комплексного тока. Модуль комплексной мощности равен полной мощности S, активная и реактивная мощности , , .

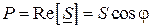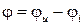Измерение действующего значения тока, напряжения в цепи синусоидального тока проводится амперметром и вольтметром электродинамической или электромагнитной системы. Активная мощность измеряется ваттметром. Ваттметр имеет две цепи (обмотки) – токовую (последовательная неподвижная обмотка) и по напряжению (параллельная подвижная обмотка). Показание ваттметра рассчитывается по формуле 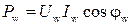, где U _w, I _w – действующие значения напряжения и тока ваттметра, а φ_w – угол сдвига фаз между ними, считая одинаковыми положительными направлениями комплексов напряжения и тока относительно зажимов, отмеченных * или • (как правило, от отмеченных зажимов к неотмеченным) (рис. 5.1).

Баланс мощностей генераторов и приемников электромагнитной энергии:

, , .

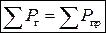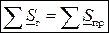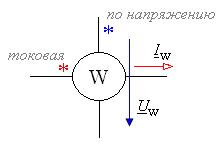
Рис. 5.1. Разметка прибора

При исследовании режимов электрических цепей наряду с аналитическими методами используют графический метод – построение геометрических мест концов вектора тока или напряжения при изменении параметров элементов электрических цепей. Эти геометрические места, называемые диаграммами (годографами) могут иметь сложную форму. В простейших случаях получают прямые линии или дуги окружностей, которые называют соответственно линейными и круговыми диаграммами. Линейная и круговая диаграмма имеют место, если при изменении параметра элемента ветви, угол сдвига между током и напряжением на этой ветви не меняется. Уравнение для некоторого комплекса (вектора) 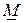, годографом которого является дуга окружности, в общем случае имеет вид 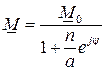. При этом только действительное число 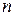является переменным, а , действительное число а и угол 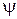остаются неизменными. 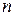В теории доказывается, что годографом комплекса при изменении в широком диапазоне является дуга окружности.

В работе при проведении эксперимента для построения круговой диаграммы комплекса входного тока пассивного двухполюсника напряжение на входе пассивного двухполюсника поддерживается неизменным, а в широком диапазоне (от "нуля" до "бесконечности") меняется параметр элемента пассивного двухполюсника. При построении годографа на комплексной плоскости, как правило, принимают комплекс входного напряжения 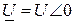, а вещественная ось располагается вертикально.

Круговая диаграмма неразветвленной цепи.

Пусть неразветвленная цепь состоит из последовательно соединенных элементов: один с неизменяющимися параметрами, другой может менять параметры в широком диапазоне. К примеру, первый элемент – резистивный с сопротивлением R, второй элемент –индуктивный L. Цепь подключена к источнику синусоидального напряжения. При изменении частоты 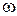входного напряжения от нуля до бесконечности меняется реактивное сопротивление w L (обозначено на схеме стрелкой). Действующее значение напряжения на входе при этом поддерживается неизменным.

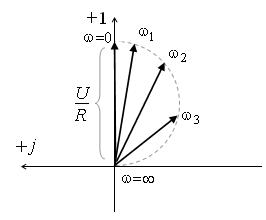
а) б)

Рис. 5.2. Неразветвленная цепь с изменяющимся параметром (а) и круговая диаграмма неразветвленной цепи (б)

Комплекс тока рассчитывается по формуле . Если U =const, то при изменении 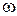и неизменности R и L выражение удовлетворяет условию круговой диаграммы.

Модуль комплекса входного тока зависит от частоты 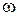: 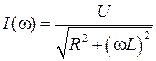. При 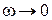ток максимален и совпадает по фазе с приложенным напряжением: 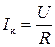, при частоте 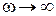ток равен нулю. Во всех остальных случаях характер цепи активно-индуктивный, т.е. комплекс тока отстает от комплекса напряжения на угол , при 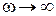ψ=90°. Годограф представляет собой половину дуги окружности радиусом 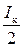, расположенной в четвертой четверти (рис. 5.2). При изменении индуктивности L от нуля до бесконечности и неизменности R и 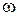выражение для комплекса тока также удовлетворяет условию круговой диаграммы. Круговая диаграмма будет аналогична круговой диаграмме на рис. 5.2. При изменении сопротивления R и неизменности L и комплекс тока рассчитывается по формуле 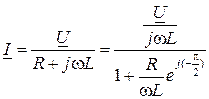, выражение также удовлетворяет условию круговой диаграммы. При R = 0 комплекс тока короткого замыкания расположен по мнимой оси 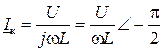, при R =∞ ток равен нулю (рис. 5.3).

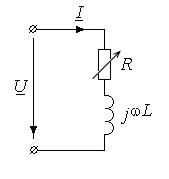
а) б)

Рис. 5.3. Неразветвленная цепь с изменяющимся параметром (а) и круговая диаграмма неразветвленной цепи (б)