Определение.
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных.
Определение.
Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.
Определение.
Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.
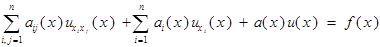 (1)
(1)
Пусть выбран любой  , где
, где  , и его норма:
, и его норма:
 - дифференциальный оператор.
- дифференциальный оператор.
 - запись линейного диф. уравнения с помощью диф. оператора. (2)
- запись линейного диф. уравнения с помощью диф. оператора. (2)
Определение.
Открытое, связное множество 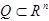 называется областью.
называется областью.
По умолчанию будем считать область ограниченной.
Через 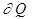 или
или  будем обозначать границу области.
будем обозначать границу области.
Определение.
 - (n-1)-мерное многообразие S в
- (n-1)-мерное многообразие S в 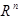 принадлежит классу
принадлежит классу 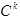 (
(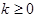 ), если
), если
для  и
и  такие, что:
такие, что:
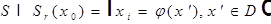 , где
, где 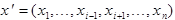
 однозначно проектируется на плоскость
однозначно проектируется на плоскость  , при этом:
, при этом:
D - проекция данного множества на плоскость  ,
,  - k раз непрерывно дифференцируема в D по всем переменным.
- k раз непрерывно дифференцируема в D по всем переменным.

Можно разбить поверхность на части, в каждой части можно одну координату выразить через другие непрерывно дифференцируемой функцией.
 - множество k раз непрерывно дифференцируемых функций в Q.
- множество k раз непрерывно дифференцируемых функций в Q.
 - множество k раз непрерывно дифференцируемых функций в
- множество k раз непрерывно дифференцируемых функций в 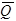 .
.
 , аналогично
, аналогично  .
.
 - множество финитных k раз непрерывно дифференцируемых функций.
- множество финитных k раз непрерывно дифференцируемых функций.
Аналогично:  .
.
§ 2. Классификация линейных уравнений в частных производных второго порядка.
 .
.
 - матрица квадратичной формы.
- матрица квадратичной формы.
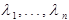 - n вещественных собственных значений матрицы A
- n вещественных собственных значений матрицы A
 - количество положительных собственных значений.
- количество положительных собственных значений.
|
|
 - количество отрицательных собственных значений.
- количество отрицательных собственных значений.
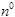 - количество нулевых собственных значений с учетом кратности.
- количество нулевых собственных значений с учетом кратности.
1.Если  = n или
= n или  = n, то это эллиптическое уравнение.
= n, то это эллиптическое уравнение.
Ex: Уравнение Пуассона
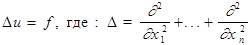 .
.
2.Если  = n - 1,
= n - 1,  = 1, или
= 1, или  = 1,
= 1,  = n - 1, то уравнение гиперболическое.
= n - 1, то уравнение гиперболическое.
Ex:  - волновое уравнение.
- волновое уравнение.
Для уравнения Лапласа:
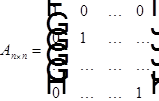
Для волнового уравнения:

3.Если  , а
, а 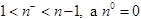 , то ультрагиперболическое уравнение.
, то ультрагиперболическое уравнение.
Ex: 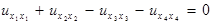 .
.
4.Если  , то параболическое уравнение.
, то параболическое уравнение.
Ex:  , и - уравнение теплопроводности.
, и - уравнение теплопроводности.
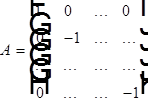
Определение.
Каноническим видом линейного дифференциального уравнения в частных производных называется такой вид, когда матрица A является диагональной.
Приведение к каноническому виду.
1) y=y(x), то:

Уравнение (1) в новой системе координат:
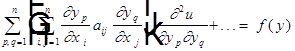 (1')
(1')
Матрица Якоби:
 .
.
В результате:

|
Ex:
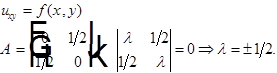
гиперболическое уравнение.
 - канонический вид волнового уравнения.
- канонический вид волнового уравнения.
Замечание: тип уравнения может быть различный в различных точках.
§ 3.Постановка начальных и краевых задач для уравнений в частных производных.
Задача Коши для волнового уравнения:


Уравнение теплопроводности


Уравнение Пуассона

Определение.
Если малые изменения правой части уравнения приводят к большим изменениям в решении, то задача считается некорректной.
 (6)
(6)
 (7.1)
(7.1)
 (7.2)
(7.2)
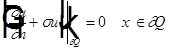 (7.3)
(7.3)
(6)(7.1) - первая краевая задача, задача Дирихле.
(6)(7.2) - вторая краевая задача, задача Неймана.
(6)(7.3) - третья краевая задача.
Волновое уравнение.
 (8)
(8)

 (9)
(9)
 (10)
(10)
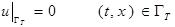 (11.1)
(11.1)
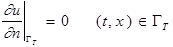 (11.2)
(11.2)
 (11.3)
(11.3)
(8) (9) (10) (11.1) - смешанные
(11.2) задачи
(11.3) (краевые задачи)
 - единичный вектор внешней нормали к поверхности.
- единичный вектор внешней нормали к поверхности.
На 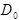 задаются начальные условия.
задаются начальные условия.
|
|
На боковой поверхности - краевые задачи.
Параболическое уравнение.
 (12)
(12)
 (13)
(13)
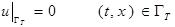 (14.1)
(14.1)
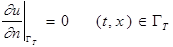 (14.2)
(14.2)
 (14.3)
(14.3)
(12) (13) (14.1) - первая, вторая и третья смешанные задачи
(14.2) для уравнения
(14.3) теплопроводности.
(14.1) - на границе задана температура;
(14.2) - задан тепловой поток;
(14.3) - задан теплообмен с окружающей средой.
§ 4. Решение смешанных задач для волнового уравнения методом Фурье (разделением переменных).
Первая смешанная задача.
 (1)
(1)
 (2)
(2)
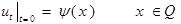 (3)
(3)
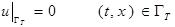 (4)
(4)
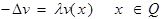 (5)
(5)
 (6)
(6)
Собственные значения (5) - (6) вещественны, имеют конечную кратность.

 - изолир.
- изолир. 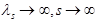 .
.
 - ортонормированный базис в
- ортонормированный базис в 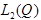 .
.
В симметричной матрице собственные вектора, соответствующие разным собственным значениям, попарно ортогональны.
Пусть функции 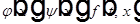 - разложены по базису
- разложены по базису 
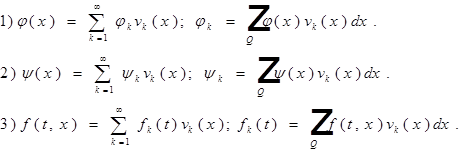
тогда и u(t,x) можно разложить по базису  :
: 
Почленно дифференцируем ряд 2 раза:

 (7)
(7)
Путём разложения решения в ряды по собственным функциям задачи алгебраизуем задачу, получаем счётное число обыкновенных дифференциальных уравнений.
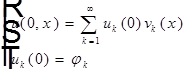 (8)
(8)
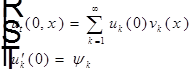 (9)
(9)
(7) (8) (9) - задача.
Решим однородное уравнение для (7):

- общее решение однородного уравнения (7)

 (10)
(10)
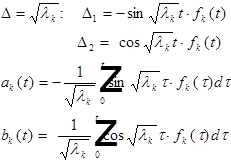
В результате:  - частное решение неоднородного уравнения (7).
- частное решение неоднородного уравнения (7).
 - общее решение уравнения (7).
- общее решение уравнения (7).
Подставим (8) и (9) в решение:
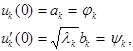
т.е. 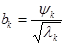 .
.
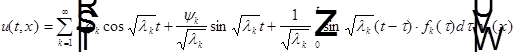
|
Замечание: не обоснована сходимость рядов.
§ 5.Решение смешанных задач уравнения теплопроводности методом Фурье (разделения переменных).
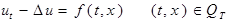 (1)
(1)
 (2)
(2)
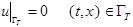 (3)
(3)
 (4)
(4)
 (5)
(5)
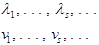 - собственные векторы и собственные значения.
- собственные векторы и собственные значения.

 (6)
(6)
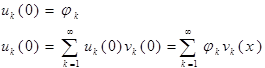
 - общее решение однородного уравнения (6)
- общее решение однородного уравнения (6)
 - частное решение неоднородного уравнения (6)
- частное решение неоднородного уравнения (6)

 - общее решение уравнения (6).
- общее решение уравнения (6).
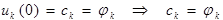

|
Рассмотрим функцию:
|
|

 - бесконечно дифференцируема при
- бесконечно дифференцируема при  .
.
Если 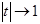 из
из  , то:
, то:
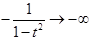
 , и при
, и при  функция склеивается как бесконечно гладкая.
функция склеивается как бесконечно гладкая.
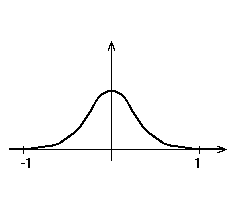
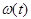 -финитная:
-финитная: 
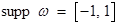 - замыкание множества, где
- замыкание множества, где  отлична от 0.
отлична от 0.
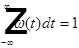 .
.
Введём  - функция n переменных.
- функция n переменных.
Свойства  :
:
1)  - бесконечно дифференцируемая, финитная:
- бесконечно дифференцируемая, финитная:
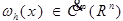 .
.
2) 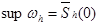 - замкнутый шар радиуса h с центром в O.
- замкнутый шар радиуса h с центром в O.
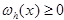 .
.
3) 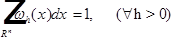
Доказательство.
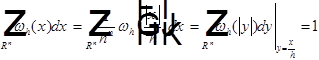 , С находится из условия
, С находится из условия  .
.
4) 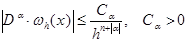 .
.
Обозначим: 


Интеграл по x бесконечно дифференцируем.

Если 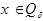 , то:
, то: 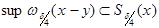
Носитель функции принадлежит области интегрирования, и:  .
.
Если  , то
, то 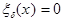 :
: 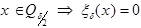 .
.
Свойства функции 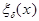 :
:


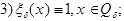
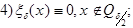
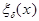 - срезающая функция.
- срезающая функция.
Пространство  .
.
Определение.
Пусть  . Назовём множество функций
. Назовём множество функций  , пространством
, пространством 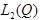 , если:
, если:
-  - измеримы в Q;
- измеримы в Q;
- 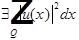 в смысле Лебега.
в смысле Лебега.
Вводится  . Выполняются все аксиомы скалярного произведения.
. Выполняются все аксиомы скалярного произведения.
Утверждение (без доказательства).
 - полное пространство.
- полное пространство.
Вводится  .
.
Свойства пространства  .
.
Теорема 1.
Множество финитных бесконечно дифференцируемых функций всюду плотно в пространстве 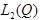 :
:
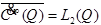 .
.
Доказательство.
Множество ступенчатых функций плотно в  .
.
Множество линейных комбинаций характеристических функций всюду плотно в 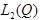 .
.
Доказать: любую характеристическую функцию измеримого множества можно сколь угодно точно аппроксимировать финитными функциями.
Любое измеримое множество сколь угодно точно может быть аппроксимировано открытыми областями.
Доказать: характеристическую функцию 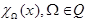 можно сколь угодно точно аппроксимировать финитными бесконечно гладкими функциями.
можно сколь угодно точно аппроксимировать финитными бесконечно гладкими функциями.
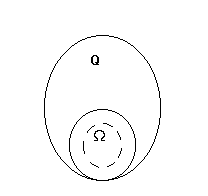

Рассмотрим 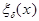 - финитная, бесконечно дифференцируема в
- финитная, бесконечно дифференцируема в 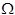 .
.

Значит,  .
.
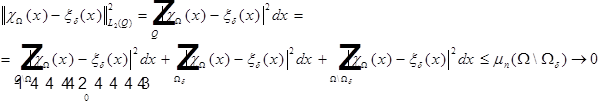
Аппроксимация получена.
Теорема 2.
Множество непрерывных функций всюду плотно в пространстве  .
.
Определение 2.
Пусть  и считается продолженной нулем вне Q
и считается продолженной нулем вне Q 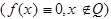 . Скажем:
. Скажем:
f - непрерывна в среднеквадратичном, если 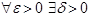 :
:
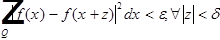 .
.

Теорема 3.
Любая функция из  непрерывна в среднеквадратичном.
непрерывна в среднеквадратичном.
Доказательство.
Пусть 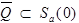 . Пусть
. Пусть 

Оценим:

При сдвиге supp сдвигается в пределах шара радиуса 2a.


Теорема доказана.
Определение 3.

 - бесконечно дифференцируема, финитна.
- бесконечно дифференцируема, финитна.

Свойства:

 - осреднение функции f.
- осреднение функции f.
Теорема 4.
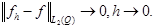
Любая функция из  сколь угодно точно аппроксимируема своими осреднениями - бесконечно дифференцируемыми, финитными в
сколь угодно точно аппроксимируема своими осреднениями - бесконечно дифференцируемыми, финитными в 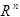 .
.
Доказательство.
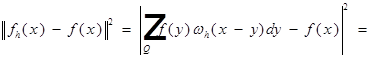
От Q к 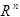 , от
, от 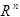 к
к 
При  .
.
Возьмем любые две функции:
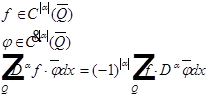
Определение.
 - множество функций, принадлежащих
- множество функций, принадлежащих  на любом компакте внутри области.
на любом компакте внутри области.

Определение 1.
Пусть 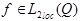
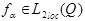 - обобщённая производная функции f, если
- обобщённая производная функции f, если  выполняется:
выполняется:
 (1)
(1)
Теорема 1.
Обобщённая производная определяется единственным образом.
Доказательство.
Предположим противное: 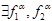 - обобщённые производные функции f.
- обобщённые производные функции f.
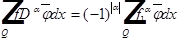 (2)
(2)
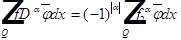 (3)
(3)
(2),(3) - тождество для 
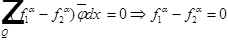 - что и требовалось доказать.
- что и требовалось доказать.
Теорема 2.
Обобщённые производные не зависят от порядка дифференцирования.
Доказательство - из интегрального тождества (1).
Примеры обобщённых производных.
Ex 1.

По определению:
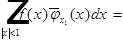
Пусть  и
и 
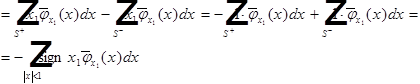

|
Ex 2.
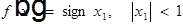
Покажем, что обобщённой производной не существует.
Пусть  , то:
, то:
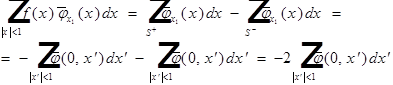
где 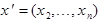
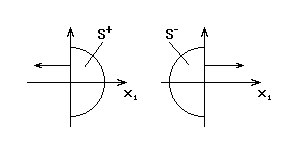
1) пусть  носитель в
носитель в  , то:
, то:
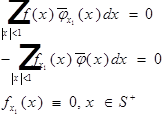
2) пусть 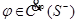 :
: 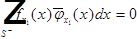 , значит:
, значит:

Вывод:  .
.

Вывод:  , не имеет обобщённой производной.
, не имеет обобщённой производной.
Теорема 3.
Пусть 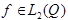 имеет обобщённую производную
имеет обобщённую производную 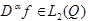 , то:
, то:
1.  (4)
(4)

если  .
.
2. Если к тому же 
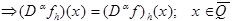 (6)
(6)
 (7)
(7)
Доказательство.
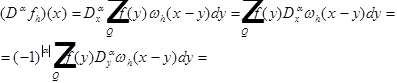
Выберем h так, чтобы 


Подсказка: если функция финитна, то её носитель - внутри области.
Если функцию умножить на срезающую, то ничего не изменится.
Теорема 4.

Утверждение.
Пусть  , то
, то 

Пусть  - открытый компакт, то
- открытый компакт, то  для
для 

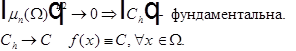
Теорема 5.
Пусть 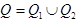 .
.  имеет обобщённые производные
имеет обобщённые производные  и
и 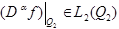 , то
, то
существует обобщённая производная  .
.
Пространство Соболева.
Определение.
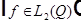 , такая, что
, такая, что  называется пространством Соболева порядка k.
называется пространством Соболева порядка k.

Обозначения: 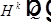 ,
, 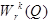 или
или  .
.
Введём  .
.
Утверждение.
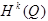 - гильбертово(унитарное, сепарабельное).
- гильбертово(унитарное, сепарабельное).
Теорема 1.
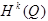 - полное пространство.
- полное пространство.
Доказательство.
 - фундаментальная в
- фундаментальная в 
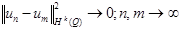
 .
.
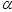 - мультииндекс
- мультииндекс
 - может быть равен 0.
- может быть равен 0.
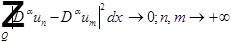
 в
в  .
.
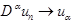 в
в  .
.
Интегральное тождество для  :
:
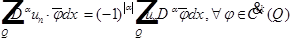
Из сильной сходимости следует слабая:
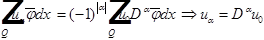

Вывод: пространство полное.
Свойства пространств Соболева.
1.  для
для  .
.
2.Если  , то
, то  .
.
3.Если  , то
, то  .
.
4.Если  , то
, то

если  , то
, то  .
.
5.  - невырожденное, k раз непрерывно дифференцируемое преобразование, отображающее
- невырожденное, k раз непрерывно дифференцируемое преобразование, отображающее 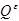 в
в 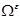 .
.
 и пусть
и пусть  .
.
Пусть 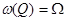 .
.
Пусть 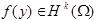 , то
, то 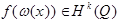 .
.
Утверждение.
Невырожденная, гладкая замена переменных сохраняет принадлежность функции пространству Соболева.
6.Обозначим  - куб со стороной 2 a с центром в начале координат.
- куб со стороной 2 a с центром в начале координат.
Множество бесконечно дифференцируемых функций замыкания куба является всюду плотным в 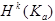 .
.
 .
.

Доказательство.
Раздвинем область, возьмём  и будем её аппроксимировать последовательностью бесконечно гладких функций.
и будем её аппроксимировать последовательностью бесконечно гладких функций.
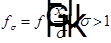 (определена в растянутом кубе)
(определена в растянутом кубе)

Оценим: 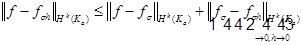

Выберем 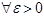 и рассмотрим
и рассмотрим 
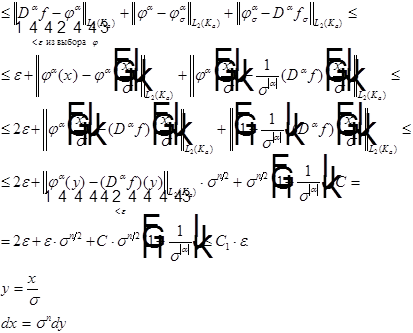
Разбиение единицы.
Теорема.
Пусть  - ограниченная область, пусть
- ограниченная область, пусть 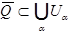 - покрытие замыкания Q,
- покрытие замыкания Q, 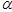 - может равняться бесконечности.
- может равняться бесконечности.
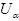 - открытые, тогда: существует конечный набор
- открытые, тогда: существует конечный набор 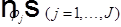 - финитные, бесконечно дифференцируемые в
- финитные, бесконечно дифференцируемые в 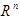 , неотрицательные функции, такие, что:
, неотрицательные функции, такие, что:

Используется для локализации свойства: U имеет свойство на 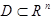 , расширяем D на
, расширяем D на  путём домножения на
путём домножения на 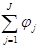 .
.
Доказательство.
Возьмём 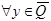 . Для
. Для 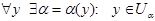 - y покрывается множеством
- y покрывается множеством 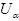 .
.
Для каждой выбранной y построим:
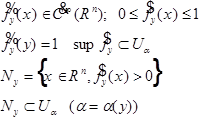
 покрывается
покрывается  . Из бесконечного покрытия выберем конечное подпокрытие:
. Из бесконечного покрытия выберем конечное подпокрытие:
 .
.
Обозначим: 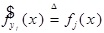 . Обозначим:
. Обозначим:  .
.
Определим:  :
:

Получили: 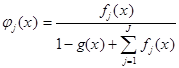 .
.
Если  , то
, то  ,
, 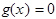 , и
, и  .
.
Знаменатель в 0 не обращается.
Построена
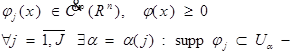 выполняется свойство 3.
выполняется свойство 3.
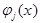 - выполняются свойства 1 и 2.
- выполняются свойства 1 и 2.
Теорема о разбиении единицы доказана.
Теорема о продолжении функции.
Частный случай - продолжение из прямоугольников.
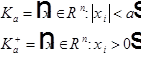
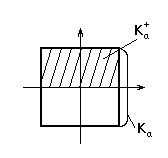
Продолжение функции из  в
в  .
.
Лемма 1.

 - продолжение функции f:
- продолжение функции f:
 и
и 
1.Определить функцию.
2.Проверить условие сливания: совпадание значений функции и её производных по  до k -го порядка.
до k -го порядка.
Доказательство.
Определим  (2)
(2)
Коэффициенты 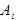 из условия:
из условия:
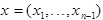
 (3)
(3)

Значит, функция непрерывна.
Теперь - доказательство совпадения производных.
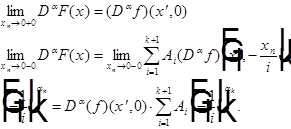
Выполняется одно уравнение из (3), и:
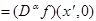 .
.
Значит: 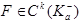 .
.
Неравенство (1) очевидно через определение нормы в  .
.
Замечание: из доказательства и свойства (6) пространств Соболева следует: можно перейти к  - пространству Соболева с выполнением этой теоремы, и (1) тоже справедливо.
- пространству Соболева с выполнением этой теоремы, и (1) тоже справедливо.
Замечание: в силу того, что множество бесконечно дифференцируемых функций в замыкании куба всюду плотно в пространстве  в этом кубе и в силу того, что протсранство Соболева инвариантно относительно невырожденной гладкой замены переменных.
в этом кубе и в силу того, что протсранство Соболева инвариантно относительно невырожденной гладкой замены переменных.
Лемма 2.

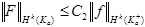 (4)
(4)
Теорема о продолжении функции.
Пусть 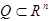 - ограниченная область, граница
- ограниченная область, граница 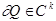 . Пусть
. Пусть 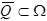 (
(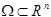 - область), тогда:
- область), тогда:
 - продолжение f, такая, что:
- продолжение f, такая, что:
1) 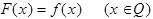
2) 
3)  (5)
(5)
Замечание.
Лемма 1 - рассмотрены кубики, в теореме: из Q на  и все свойства, как в лемме 1.
и все свойства, как в лемме 1.

Доказательство.

В окрестности каждой точки границы:  нарисуем шар
нарисуем шар  .
.
Пусть в O(z) граница задаётся уравнением  .
.
Введём новые переменные:
 - невырожденное преобразование координат.
- невырожденное преобразование координат.
Преобразование:  - внутри пространства Соболева.
- внутри пространства Соболева.
Во что перейдёт множество: 
Вырезали куб  .
.

Результат преобразования
Прообраз куба  - криволинейный кубик.
- криволинейный кубик.
Покроем границу кубиками Vi и выберем конечное подпокрытие.
(Tju)(y) = u(x(y)) (xVj) - переход от x к y,
переход от y к x: 
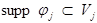
Введём: 
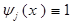 если
если 

 на носителях
на носителях  обратятся в 1.
обратятся в 1.
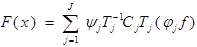
Свойства оператора продолжения:
1. F(x) - ограниченный оператор;
2. Т.к.  - финитная, то F(x) - финитная на
- финитная, то F(x) - финитная на
Доказать: F(x)=f(x),если  .
.
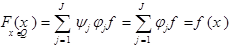
Замечание.
Теорема 1 остаётся справедливой для пространств  (следует из доказательства).
(следует из доказательства).
Теорема 2.
Пусть  - ограниченная область
- ограниченная область
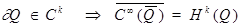 ,
, 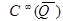 - всюду плотно в
- всюду плотно в  .
.
Доказательство.
Рассмотрим произвольную функцию  .
.
 - ограниченная.
- ограниченная.
F -продолжение f. Так как F - финитная в, то 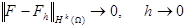
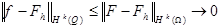
Сепарабельность пространств Соболева.
Теорема.
Пусть  - ограниченная область,
- ограниченная область,  , тогда:
, тогда:
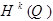 - сепарабельное.
- сепарабельное.
Построениe счётного всюду плотного множества.
Доказательство.
Рассмотрим  ; продолжение функции f:
; продолжение функции f:  .
.
Аппроксимируем функцию F. Множество финитных, бесконечно дифференцируемых функций (в силу свойств осреднений) всюду плотно в пространстве финитных функций  .
.
Очевидно:  .
.
Где коэффициенты: 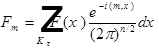 .
.
Пусть H - сепарабельное гильбертово пространство.
Определение.
Функции 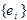 образуют ортонормированную систему, если
образуют ортонормированную систему, если  , и
, и  .
.
Утверждение.
В каждом сепарабельном гильбертовом пространстве существует ортонормированный базис, т.е. такая система 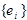 ,что
,что  .
.
Разложение по этому базису единственно, и: 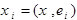 .
.
Равенство Парсеваля.
 .
.
Пространство  - сепарабельное гильбертово пространство с ортонормированным базисом: можно взять систему экспонент (нормированную).
- сепарабельное гильбертово пространство с ортонормированным базисом: можно взять систему экспонент (нормированную).
Разложение в сходящийся ряд:

Определим вид коэффициентов Фурье:
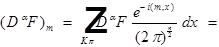
проинтегрируем по частям и получим:
 , где
, где 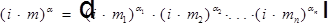
Получаем: 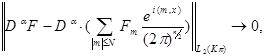 и следовательно:
и следовательно: