Графическое изображение распределения давления покоящейся жидкости по какой-либо поверхности называется эпюрой гидростатического давления (рис. 2.8). Закон распределения давления в покоящейся жидкости определяется основным уравнением гидростатического давления
.
Из уравнения видно, что давление p является линейной функцией глубины h погружения точки под уровнем свободной поверхности (po=const; g=const). Значит давление p=f(h) изменяется с глубиной по закону прямой линии. Указанное свойство гидростатического давления позволяет весьма просто строить эпюру давления.
Построим эпюру гидростатического давления для простейшего случая – избыточного давления жидкости на плоскую прямоугольную стенку (рис. 2.8).
Избыточное давление в каждой точке стенки определяется выражением pизб=gh и равно:
pизб=0 – на свободной поверхности при h =0;
pизб=gH – у дна при h=H.
Суммарное давление жидкости на всю поверхность равно площади эпюры давления, умноженной на ширину b данной прямоугольной поверхности:
Положение центра давления определяется положением центра тяжести эпюры, через который пройдет сила P суммарного давления. Необходимо провести через центр тяжести эпюры перпендикуляр к поверхности, точка пересечения его с поверхностью будет центром давления.
Эпюры дают возможность наглядно представить нагрузку от жидкости на ту или иную поверхность и широко используются при решении практических задач. Способ определения величины суммарного давления жидкости на основе эпюры давления называется графоаналитическим.
Способы выражения гидростатического давления.
Величина гидростатического давления (полного или избыточного) может быть выражена тремя способами:
|
|
- в единицах силы, действующей на единицу площади, например,
;
- в атмосферах; в гидравлике используется техническая атмосфера, равная
;
давление, выраженное в атмосферах, обозначают ата (абсолютное давление), ати (избыточное давление) и атв (вакуумметрическое давление);
- высотой столба жидкости, м.
Для уяснения последнего, практически важного, способа выражения давления преобразуем основное уравнение гидростатического давления
поделив его на g. Получим:
.
В этом уравнении все члены имеют размерность длины и выражают высоту столба жидкости, соответствующую тому или иному давлению. Действительно
.
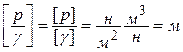Величина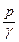 
называется пьезометрической высотой, соответствующей давлению p.
Закон Архимеда
Закон Архимеда - это закон, согласно которому на всякое тело, погруженное в жидкость (или газ), действует со стороны этой жидкости (газа) поддерживающая сила, равная весу вытесненной телом жидкости (газа), направленная вверх и приложенная к центру тяжести вытесненного объёма (рис. 2.12).
(2.19)
где V – объем погруженного тела.
Рис. 2.12. Поддерживающая сила
Сила F называется поддерживающей силой; ее также называют также архимедовой, или силой водоизмещения, или гидростатической подъёмной силой.
Если вес тела P меньше поддерживающей силы F, тело всплывает на поверхность жидкости до тех пор, пока вес вытесненной погруженной частью тела жидкости не станет равным поддерживающей силе. Если вес тела больше поддерживающей силы, тело тонет; если же вес тела равен поддерживающей силе, тело плавает внутри жидкости.
|
|
Плавание тел
Плавание тел – это состояние равновесия твёрдого тела, частично или полностью погруженного в жидкость (или газ). Основная задача теории плавания тел - определение положений равновесия тела, погруженного в жидкость, выяснение условий устойчивости равновесия. Простейшие условия плавания тел указывает закон Архимеда.
Для однородного тела, плавающего на поверхности, справедливо соотношение
где: V - объем плавающего тела; ρ m - плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления d) - центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.14).
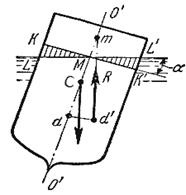
Рис. 2.14. Поперечный профиль судна
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC=h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
|
|
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h <0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести C и, чем больше метацентрическая высота h, тем больше будет остойчивость судна.