Электромагнитные механизмы
Основные сведения и классификация
Составной частью многих электрических аппаратов являются электромагнитные системы, выполненные обычно в виде электромагнитных механизмов или устройств.
Электромагнитный механизм – это электромагнитная система, подвижная часть которой совершает полезную работу при перемещении. Причем это перемещение происходит вследствие изменения или перераспределения магнитного потока (электромагниты, электромагнитные муфты и др.).
Электромагнитным устройством называют электромагнитную систему, в обмотках которой при изменении и распределении магнитного потока изменяется величина тока и напряжения (силовые измерительные трансформаторы, дроссели, магнитные усилители и др.).
Следовательно, электромагнитные механизмы предназначены для преобразования магнитной энергии в механическую.
Электромагнитные механизмы классифицируются следующим образом:
· по способу действия – удерживающие, притягивающие;
· по тепловому режиму работы – механизмы длительного, кратковременного и повторно-кратковременного режима;
· по току – постоянного и переменного тока;
· по конструкции магнитопровода – с замкнутым магнитопроводом, с разомкнутым магнитопроводом;
· по способу включения катушки – с параллельной катушкой, с последовательной катушкой.
К электромагнитным механизмам предъявляются следующие требования. Катушка электромагнита должна: обеспечивать включение электромагнитного механизма в худших условиях (нагретом состоянии и при пониженном напряжении); не перегреваться во всех режимах; быть минимальной по размеру и технологичной; механически прочной; иметь соответствующий класс изоляции согласно условиям эксплуатации.
|
|
При расчете электромагнита должны быть определены: сопротивление, число витков и диаметр провода.
Основные части и конструкции
электромагнитных механизмов
Основными элементами электромагнитной системы являются одна или несколько обмоток и магнитная цепь.
В трансформаторах одна обмотка служит для создания магнитного потока, который пересекает другую обмотку и индуктирует в ней э.д.с. В магнитных усилителях изменение тока в обмотке 1 приводит к изменению сопротивления обмотки 2 и, как следствие, величины тока в обмотке 2. В электромагнитных устройствах магнитная цепь 3 обычно не имеет воздушного зазора и выполняется либо в виде тороида, либо имеет специальную форму в результате набора из отдельных пластин
В электромагнитных механизмах магнитная цепь имеет подвижную часть (якорь 1). При перемещении якорь совершает полезную работу и притягивается к сердечнику 2. Ярмо 3 – не-подвижная часть магнитной цепи, соединяющая сердечник и якорь или несколько сердечников; d – расстояние между якорем и сердечником, называется рабочим воздушным зазором.
Создаваемый обмоткой полный магнитный поток состоит из: потока Ф – рабочий магнитный поток, который проходит вдоль всей магнитной цепи лишь частично и замыкается по воздуху через расположенные поблизости детали конструкции; потока Фs – поток рассеяния, который с увеличением воздушного зазора и повышением насыщения магнитной цепи увеличивается; потока Ф d – главный рабочий поток, который проходит через рабочий воздушный зазор d (именно этот поток обусловливает возникновение механических сил, вызывающих перемещение якоря).
|
|
По конструкции катушка может быть каркасная или бескаркасная, наматываться на съемный шаблон.
Сердечник и ярмо электромагнита, образующие магнитопровод, выполняются из магнитомягких материалов с узкой петлей гистерезиса и высокой магнитной проницаемостью (m).
Одна из основных задач проектирования электромагнитов – определение электромагнитной (тяговой) силы, которую электромагнит должен развить при определенном воздушном зазоре между якорем и сердечником магнитопровода.
При подключении катушки электромагнита к источнику напряжения в ней возникает переходной процесс, описываемый уравнением
,
где i – ток в катушке; R – омическое сопротивление катушки;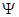 
– потокосцепление.
Умножив каждый член уравнения (6) на idt, получим выражение энергетического баланса электромагнита за время dt
Левая часть уравнения представляет собой энергию, получаемую из сети за время dt; первый член правой части – потерю энергии в омическом сопротивлении катушки; второй член правой части – приращение энергии магнитного поля в электромагните (т.е. энергию, затрачиваемую на создание магнитного поля).
В общем случае зависимость Y = f (i)имеет нелинейный характер, причем при больших зазорах эта зависимость сравнительно пологая, а при малых зазорах – более крутая.
Энергия, запасенная в поле электромагнита в момент трогания якоря,
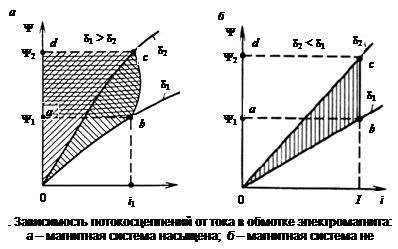
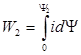
Энергия, запасенная в поле электромагнита, к концу движения якоря
|
|
Энергия, сообщенная электромагниту за время движения якоря (т.е. при уменьшении воздушного зазора от d1 до d2),
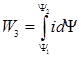
Следовательно, при уменьшении воздушного зазора от d1до d2магнитная энергия изменяется на величину
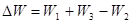Это изменение магнитной энергии равно механической работе, совершаемой движущимся якорем электромагнита: 
, где F – среднее значение тяговой силы на участке 
.
Из последнего выражения следует, что
. Таким образом, для определения тяговой силы электромагнита, исходя из энергетического баланса электромагнита, необходимо располагать зависимостями Y = f (i), построенными для различных положений якоря, и определить изменение магнитной энергии.
При отсутствии насыщения магнитной системы зависимость Y = f (i) практически прямолинейна При медленном перемещении якоря, когда ток I в катушке, достигнув установившегося значения, остается величиной постоянной, тяговая сила может быть определена по аналитической формуле. Из рис.9, б следует
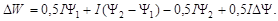
Тяговая сила в джоулях на сантиметр!
,
в килограммах
При равномерном распределении магнитного потока в воздушном зазоре для определения силы тяги при полностью притянутом якоре (или в предварительных расчетах) используется формула Максвелла. Сила тяги в килограммах электромагнита постоянного тока может быть определена из формулы Максвелла
F = 4,06×108 
,
где 
– индукция в воздушном зазоре, Вб/см2; S – поверхность полюса, взаимодействующая с магнитным потоком, см2.
Сила тяги электромагнитов переменного тока определяется их тех же методических предпосылок, но с учетом того, что магнитный поток периодически изменяется по величине и напряжению: 
. Тогда сила тяги
F = 4,06×108 
.Известно, что sin2w t = 
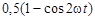, тогда F = (2,03×108 
.
Следовательно, сила тяги электромагнита переменного тока содержит две составляющие: постоянную 
и переменную 
. Переменная составляющая изменяется во времени по закону cos2w t и имеет амплитуду, равную постоянной составляющей.
Сила F имеет пульсирующий характер и дважды за период проходит через ноль. Среднее значение силы тяги за период равно ее постоянной составляющей: F ср = = 2,03×108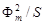 
.
Сравнивая выражения для силы тяги при постоянном и переменном токе, можно видеть, что среднее значение силы тяги при переменном токе равно силе тяги при постоянном токе.
Силу тяги электромагнита переменного тока можно определить на основе анализа его энергетического баланса. Последовательность рассмотрения аналогична, что и для магнитов постоянного тока, однако при допущении, что магнитная система не насыщена и зависимости Y = f (i)– линейны
При параллельном включении катушки электромагнита уменьшение воздушного зазора сопровождается уменьшением м.д.с. при условии постоянства потокосцепления. В этом случае изменение магнитной энергии определяется площадью треугольника Оbс:
Общее выражение для силы тяги
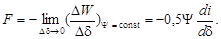Учтем, что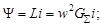 
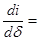
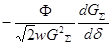, где G S – суммарная магнитная проницаемость всех воздушных зазоров; w – число витков катушки.
Тогда сила тяги в джоулях на сантиметр и килограммах соответственно
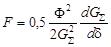и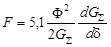 
. Если выразить магнитный поток через напряжение сети: 
, то для силы тяги запишем
