Примеры решения типовых задач

Пример 1 Расчет разветвленной цепи постоянного тока. Для схемы, приведенной на рисунке определить эквивалентное сопротивление.

Решение.

Задача относится к теме «Электрические цепи постоянного тока.

1. Разобьем цепь на участки с только последовательным или только параллельным соединением. Определим общее сопротивления участка с резисторами R₃ и R₄, которые соединены между собой последовательно, а с резистором R₅параллельно:

 

R₃₄=R₃+R₄=10+5=15 Ом

2. Заменим участок цепи с сопротивлениями R₃, R₄ и R₅ одним резистором R₃₄₅.

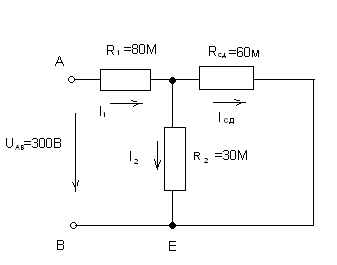
3. Резистор R₃₄₅ и R₂ включены параллельно:

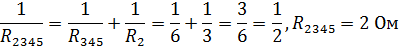
4. Заменим участок цепи с сопротивлениями R₃₄₅ и R₂ одним резистором R₂₃₄₅.

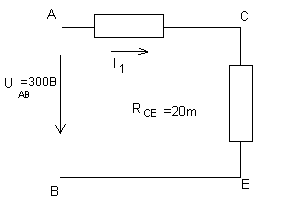
5.Находим общее сопротивление всей цепи. Резисторы R₁ и R₂₃₄₅ соединены последовательно:

 

R=R₁+R₂₃₄₅=8+2=10 Ом

Пример 2

Расчет неразветвленной цепи переменного тока.

В неразветвленной цепи переменного тока R₁=2Ом, R₂=4Ом, Х_L1=4Ом, Х_L2=6Ом, Х_С1=2Ом. Напряжение U=40B
Определить: полное сопротивление Z, ток I, коэффициент мощности cosφ, полную мощность S, активную мощность P, реактивную мощность Q. Построить в масштабе векторную диаграмму.

Решение:

1. Полное сопротивление цепи определяется по формуле:

,

где - суммарное активное сопротивление цепи. - сумма индуктивных и емкостных сопротивлений.

Тогда: .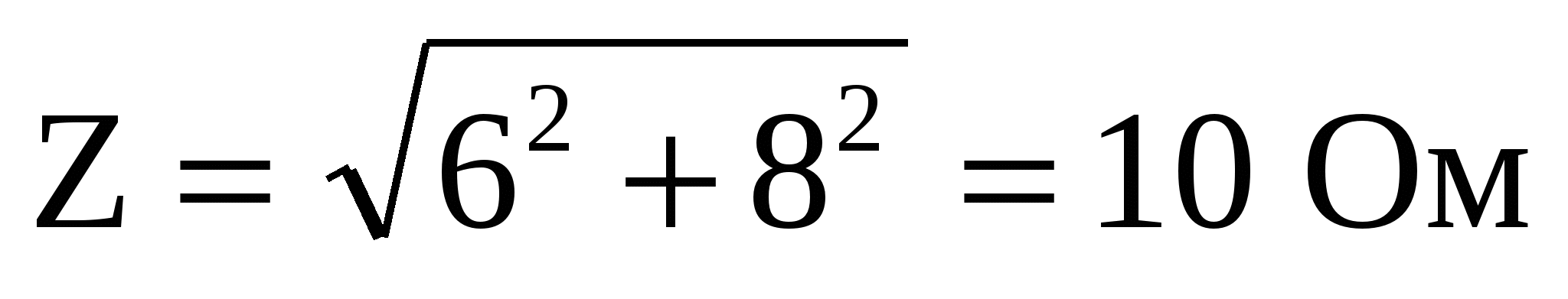

2. По закону Ома для цепи переменного тока находим ток в цепи:

3. Коэффициент мощности :

4. Определяем полную мощность:

5.Активная мощность:

6. Реактивная мощность:

7. Для построения векторной диаграммы определим падение напряжения на сопротивлениях:

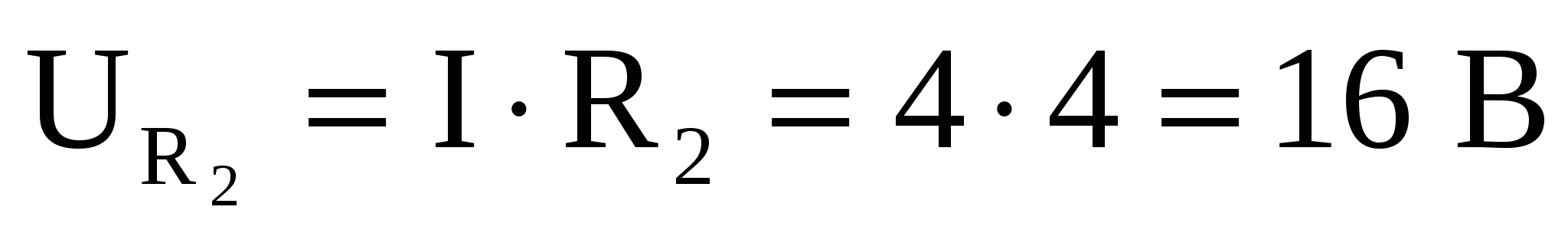
Для рассматриваемого примера задаемся масштабом:

по току:

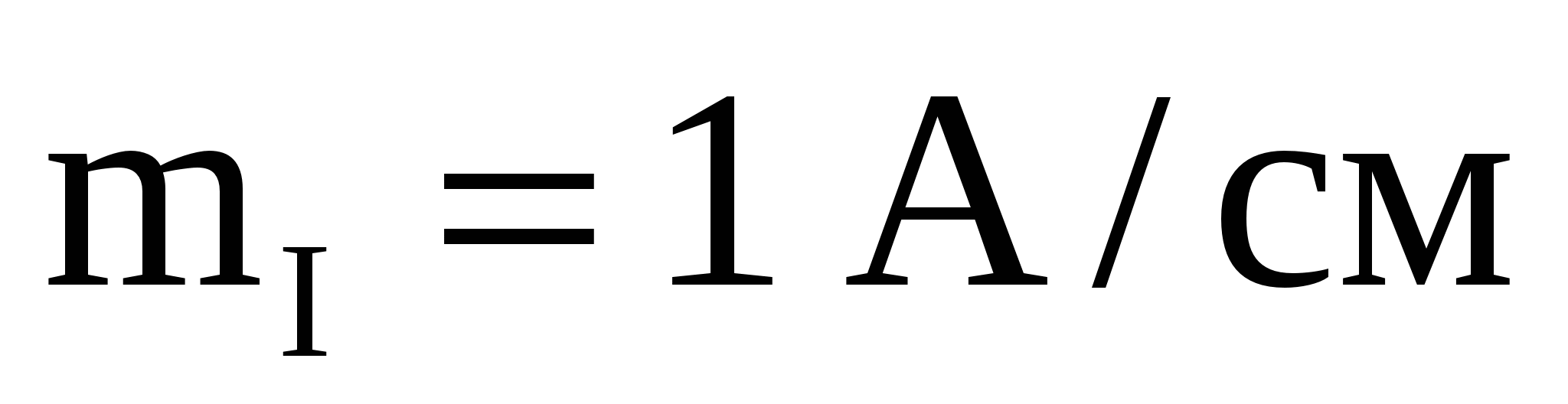
По напряжению:

Тогда длина вектора тока:

Длина векторов напряжений:

Поскольку ток является одинаковой величиной для всех сопротивлений, диаграмму строим относительно вектора тока.

1. Горизонтально в масштабе откладываем вектор тока;

2. Вдоль вектора тока откладываем векторы и ;

3. Под углом 90^о откладываем векторы напряжения и в сторону опережения вектора тока (вверх), т.к. положительное вращение векторов принято против часовой стрелки;

4. Под углом 90^о к вектору тока откладываем вниз вектор напряжения на емкостном сопротивлении.

5. Векторы , , , и 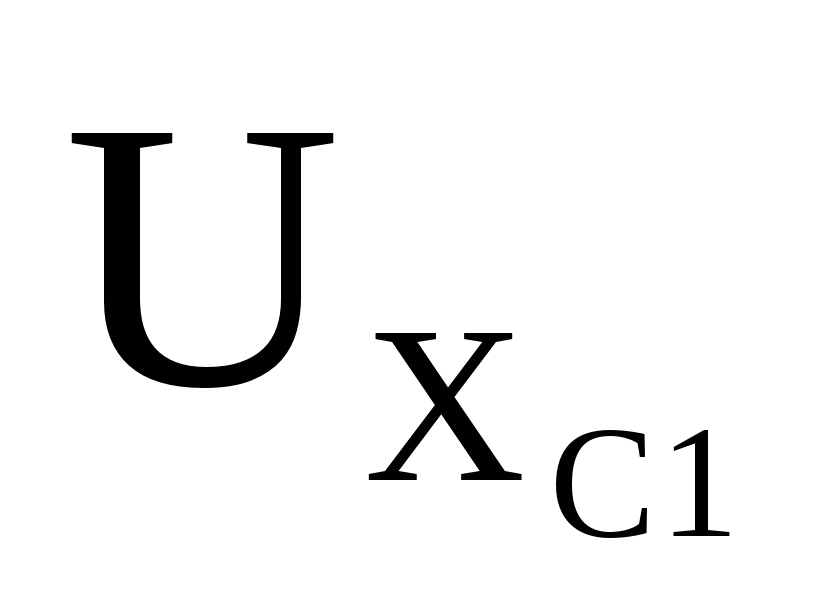, складываем по правилу сложения векторов, в результате чего получаем вектор приложенного напряжения:

6.

7. Угол φ между векторами общего напряжения и тока I называется углом сдвига фаз между током и напряжением.

8. По виду векторной диаграммы необходимо научится определять характер нагрузки. В нашем случае напряжение опережает ток: нагрузка имеет активно-индуктивный характер.

Пример 3
Расчет разветвленной цепи переменного тока

Катушка с активным сопротивлением R₁=4 Ом и индуктивным X_L1=3 Ом соединена параллельно с конденсатором, емкостное сопротивление которого X_c2=8 Ом и активным сопротивлением R₂=6 Ом. К цепи приложено напряжение U=60 В.

Определить:

1. Точки в ветвях и в неразветвленной части цепи;

2. Активные и реактивные мощности каждой ветви и всей цепи;

3. Полную мощность цепи;

4. Углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи.

Начертить в масштабе векторную диаграмму

.

Решение:

1. Определить токи в ветвях:

2. Углы сдвига фаз в ветвях:

По таблицам Брадиса находим φ₁=36^о50`, т.к. φ₁>0, то напряжение опережает ток;

;

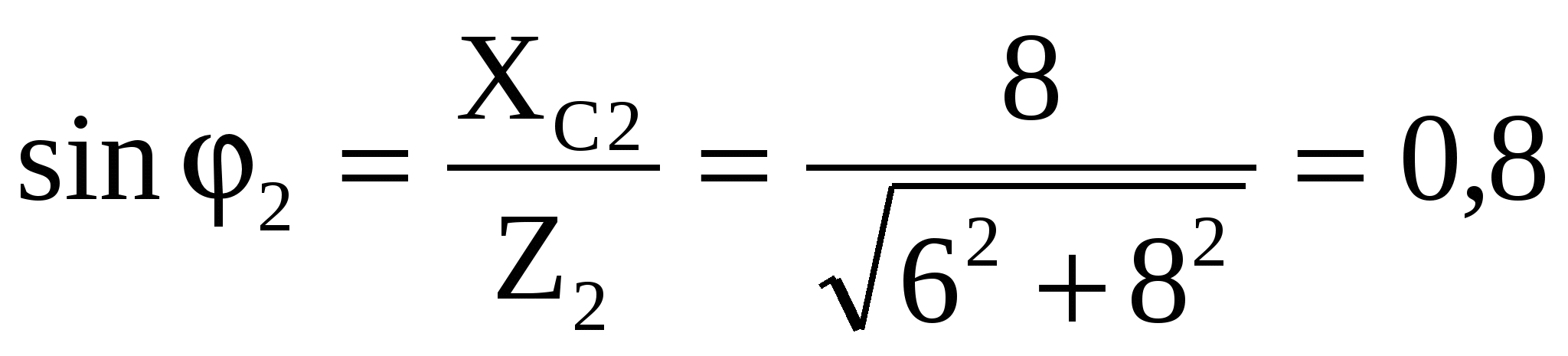φ₂=-53^о10`, т.е. напряжение отстает от тока, так как φ₂<0.

По таблицам Брадиса находим:

3. Определяем активные и реактивные составляющие токов в ветвях:

4. Определяем ток в неразветвленной части цепи

5. Определяем коэффициент мощности всей цепи:

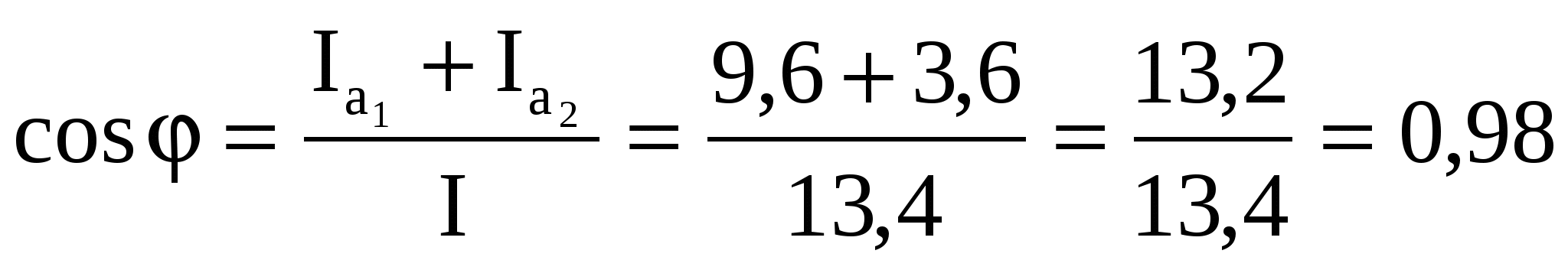
6. Определяем активные и реактивные мощности ветвей по всей цепи:

7. Определяем полную мощность всей цепи:

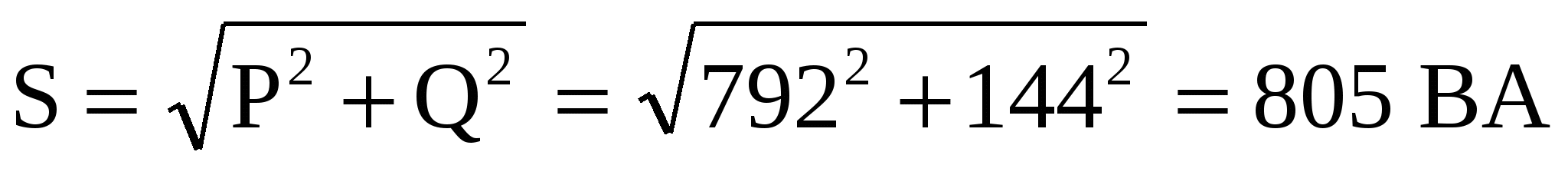
Ток в неразветвленной части цепи можно определить и таким образом:

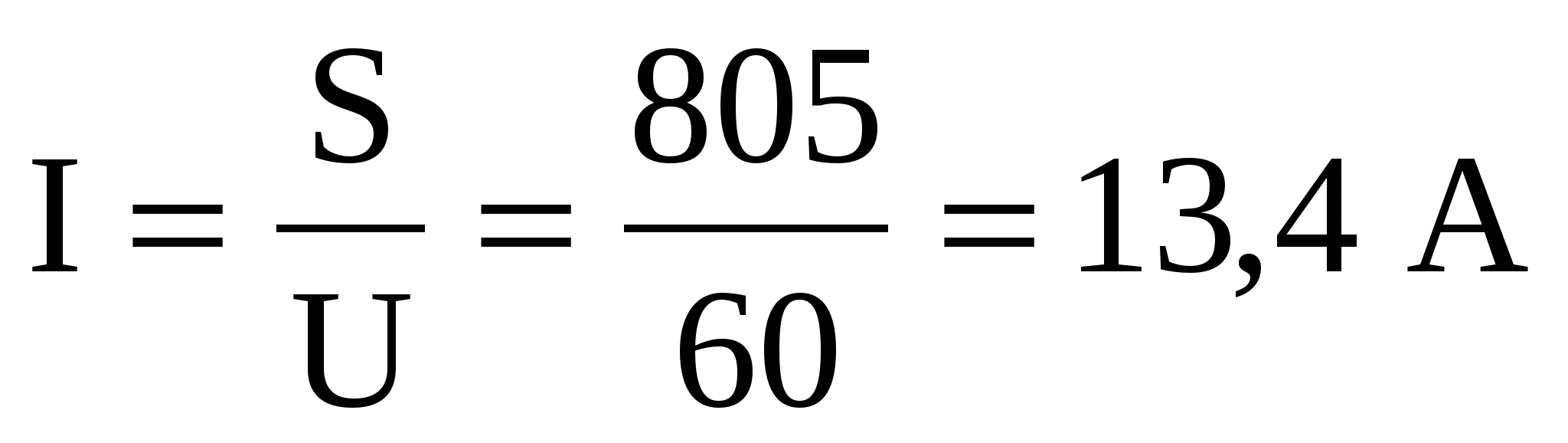
8. Для построения векторной диаграммы задаемся масштабом по току и напряжению:

1 см – 2 А

1 см – 5 В

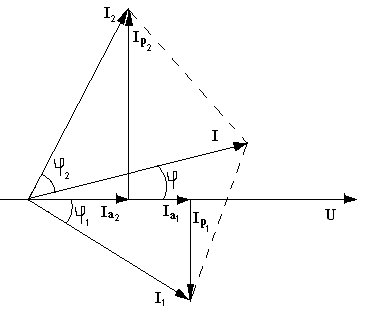
Построение начинаем с вектора напряжения U. Под углом φ₁ к нему (в сторону отставания) откладываем в масштабе тока вектора I₁, под углом φ₂ (в сторону опережения) – вектор тока I₂. Геометрическая сумма этих токов равна току в неразветвленной части цепи.

Пример 4
Расчет трехфазной цепи переменного тока.

В трёхфазную четырёхпроводную сеть включили звездой несимметричную нагрузку: в фазу А – активное сопротивление R_А = 11 Ом, в фазу B – ёмкостное сопротивление X_В = 10 Ом, в фазу C – активное сопротивление R_С = и индуктивное X_С= 6 Ом. Линейное напряжение сети U_Н = 380 В.
Определить фазные токи, активную, реактивную и полную мощности, потребляемые цепью, значения фазных углов, начертить в масштабе векторную диаграмму цепи и найти графический ток в нулевом проводе.

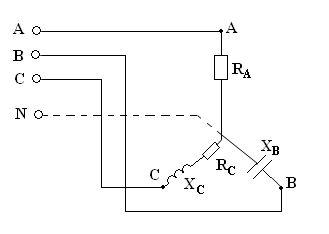
Решение.
1. Определяем фазные напяжения:

2. Находим фазные токи:

где

3. Определяем значения фазных углов:



4. Активные мощности в фазах:



Активная мощность всей цепи:

Реактивная мощность в фазах:



Реактивная мощность всей цепи:

Полная мощность всей цепи:

Для построения векторной диаграммы выбираем масштаб по току и по напряжению:
1 см – 10 А
1 см – 50 В
Построение начинаем с векторов фазных напряжений U_A, U_B, U_C располагая их под углом 120^о друг относительно друга.
Затем в принятом масштабе откладываем векторы разных токов.
Ток I_Aсовпадает с напряжением U_A.
Ток I_Bопережает напряжение U_B на угол 90^о
Ток I_C отстает от напряжения U_C на угол 36^о50`

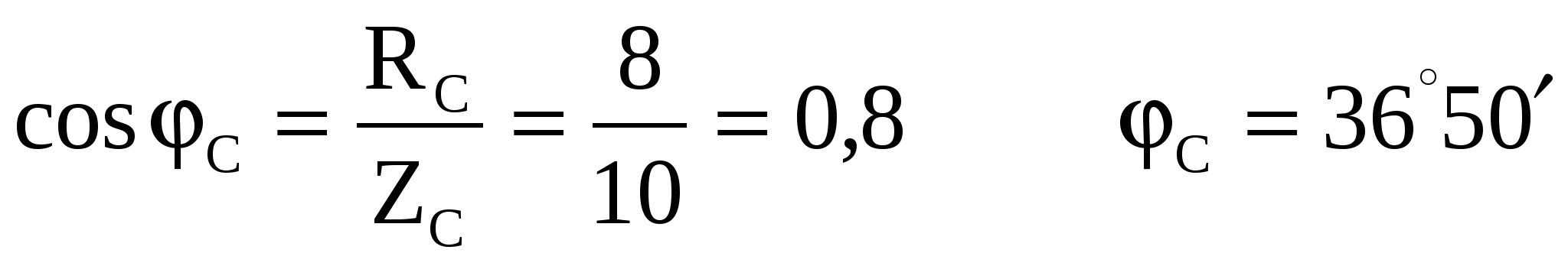
Ток в нулевом проводе равен геометрической сумме трех фазных токов

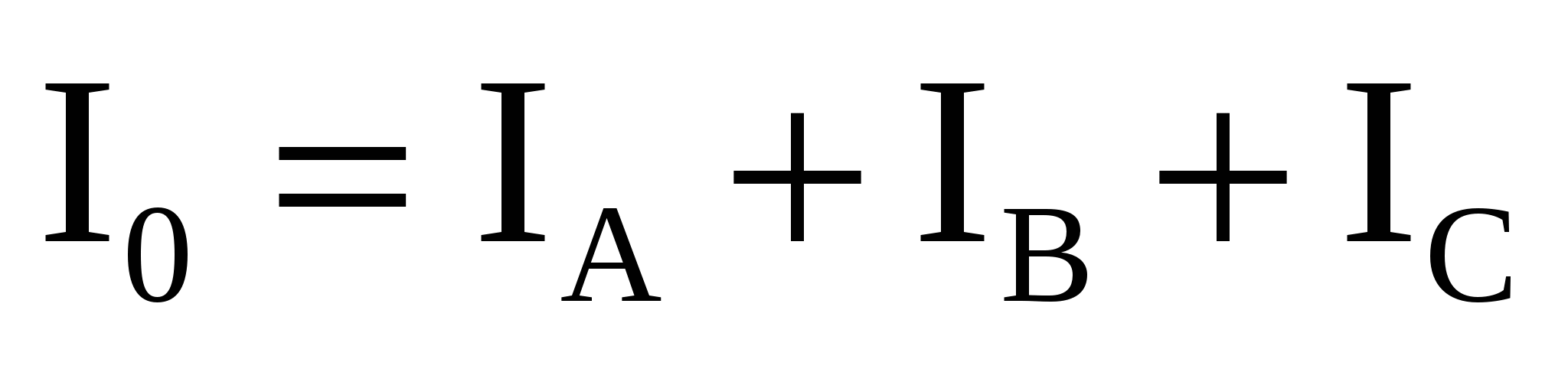
Измеряя длину вектора тока I₀, которая оказалась равной 4 см, находим ток: