4.1. Определение наблюдательности и управляемости объекта
cu1=ctrb(A1,B1)
cu1 =
Columns 1 through 8
0 0 0 0.0410 0.2268 0.0000 0.0472 0.0708
0.2268 0.0000 0.0472 0.0417 -0.1911 -0.0288 -0.0388 0.0086
-0.1911 -0.0288 -0.0388 0 0 0 0 0
Columns 9 through 12
-0.0301 -0.0288 -0.0053 0.0588
0.0474 0.0000 0.0099 0.0148
0 0 0 0
upr1=rank(cu1)
upr1 = 3
ak1=rank(A1)
ak1 = 2
cu2=obsv(A1,C1)
cu2 =
1.0000 0 0
0.7099 1.0000 0
0.7129 0.7099 1.0000
nab1=rank(cu2)
nab1 = 3
Т.к. upr1 не равен nab1 и ak1, то объект неуправляемый и не наблюдаемый.
cu1=ctrb(A2,B2)
cu1 =
Columns 1 through 8
-0.3135 -0.4384 -0.0264 0.0725 0.1172 0.1373 -0.0454 -0.3154
1.0350 1.4208 0.0319 -0.5277 -0.4372 -0.3580 0.0721 0.8865
-0.9390 -1.0598 0.0298 1.0026 0.5494 0.1133 0.0341 -0.6220
-0.3717 -1.1748 -0.0435 -0.4089 -0.1407 0.4189 -0.0979 -0.4135
0.9954 2.0077 -0.0021 -0.6763 -0.2487 -0.3584 0.0198 0.7510
-0.3201 -0.4583 0.0137 0.7675 0.1980 -0.0578 0.0300 -0.3273
-0.1973 -0.6106 -0.0033 -0.2359 -0.0286 0.1353 -0.0133 0.0361
0.1267 0.3525 -0.0002 0.0002 -0.0120 -0.0300 0.0002 0.0053
-0.0141 -0.0329 0.0001 0.0057 0.0024 -0.0010 0.0003 -0.0006
-0.0014 -0.0063 0.0000 0.0003 0.0002 0.0003 0.0000 -0.0000
>> upr1=rank(cu1)
upr1 = 8
ak1=rank(A2)
ak1 =10
cu2=obsv(A2,C2)
cu2 =
Columns 1 through 8
1.0000 0 0 0 0 0 0 0
2.9276 1.0000 0 0 0 0 0 0
6.9701 2.9276 1.0000 0 0 0 0 0
12.7809 6.9701 2.9276 1.0000 0 0 0 0
21.2817 12.7809 6.9701 2.9276 1.0000 0 0 0
31.7472 21.2817 12.7809 6.9701 2.9276 1.0000 0 0
44.6548 31.7472 21.2817 12.7809 6.9701 2.9276 1.0000 0
58.9152 44.6548 31.7472 21.2817 12.7809 6.9701 2.9276 1.0000
74.5873 58.9152 44.6548 31.7472 21.2817 12.7809 6.9701 2.9276
90.3578 74.5873 58.9152 44.6548 31.7472 21.2817 12.7809 6.9701
nab1=rank(cu2)
nab1 =10
Т.к. upr1 не равен ak1, а nab1= ak1 и, то объект неуправляемый и наблюдаемый.
4.2. Определение значений выхода и ошибки модели
e1=pe(z,th1)
e1 =0.0000
-0.0781
0.1632
0.8816
0.3781
-0.0241
0.1880
-1.4342
-0.3981
0.1787
-0.4620
0.9608
[ym1,fit1]=compare(z,th1)
ym1 = [60x1x0 iddata]
fit1 = 17.8913
e2=pe(z,th2)
e2 =
0.0007
0.0202
0.1495
0.0728
-0.7864
-0.6622
0.0645
0.0818
1.3347
-0.2330
-0.0435
2.3347
[ym1,fit1]=compare(z,th2)
ym1 = [60x1x0 iddata]
fit1 = -8.8126
plot(e2,'r') plot(e1,'g')
Рис. 21 – График выхода модели и стандартных отклонений
4.2. Построение графика выхода объекта и динамической модели
compare(z,th1)
compare(z,th2)
Рис. 22 – График выхода объекта и динамической ARMAX-модели
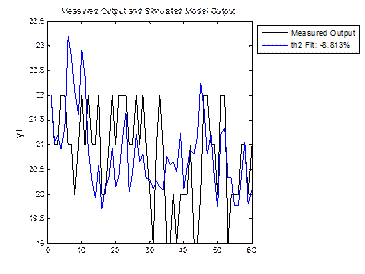
Рис. 23 – График выхода объекта и динамической BJ-модели
Приложение
Теоретические сведения
ЗАДАНИЕ 1. Анализ статистических характеристик объекта по данным пассивного эксперимента и выбор структуры модели.
Характеристики случайных процессов
При решении задач идентификации и диагностики зачастую приходится иметь дело с сигналами, представляющими собой случайные процессы. Возникает задача расчета статистических характеристик, причем в качестве исходной информации используются дискретные значения, снятые через определенный интервал дискретизации.
Основные статистические характеристики:
Математическое ожидание. Допустим, на определенном интервале времени получена выборка N значений процесса x 1, х 2, …, хN. Среднее значение, или математическое ожидание, находим по формуле
.
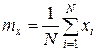Если известны частоты pj, с которыми в выборке присутствуют значения хj, то формула для расчета математического ожидания примет такой вид:
,
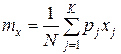где K – число групп чисел в выборке, которые отличаются друг от друга.
Дисперсия. С помощью дисперсии можно оценить разброс относительно среднего.
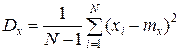или 
.
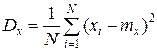Среднеквадратическое отклонение σ(СКО). СКО несет в себе ту же информацию, что и дисперсия, но измеряется в тех же единицах, что и исследуемый процесс.
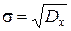или 
.
Коэффициент корреляции (или ковариации) rxy. Иногда используется термин «парный коэффициент корреляции». Он характеризует степень тесноты связи между переменными х и у:
.
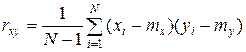Применяется также обозначение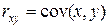 
. Эту характеристику нельзя применять для сравнительной оценки тесноты связи разных параметров, т. к. полученные значения будут зависеть от единиц измерения этих параметров, а они могут быть абсолютно различными.
Статистические функции в Matlab
mean(x) – вычисляет средние значения элементов столбцов, если х – вектор из n элементов, то вычисляется 
.
Функция median(X) – определяет срединные значения (медианы) элементов массива. В случае одномерного массива возвращает значение срединного элемента; в случае двумерного массива – это вектор-строка, содержащая значение срединных элементов каждого столбца. Таким образом, median(median(X)) – это срединный элемент (медиана) массива, что совпадает со значением median(X(:)).
std(x) – стандартное (среднеквадратичное) отклонение значений элементов столбцов, если х – вектор из n элементов, то вычисляется
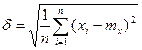
Команда plot служит для построения графиков функций в декартовой системе координат.
plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.
Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы служит функция hist, записываемая в следующем виде:
N=hist(Y) — возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y — матрица, то выдается массив данных о числе попаданий для каждого из ее столбцов.
R = corrcoef(X) функция предназначена для расчета матрицы парных коэффициентов корреляции R выборок представленных в виде матрицы Х. Наблюдения располагаются построчно в матрице Х, выборки - по столбцам.
1) Проверка стационарности данных по критерию серий
Критерий серий Вальда-Вольфовица представляет собой непараметрическую альтернативу t-критерию для независимых выборок. Данные имеют тот же вид, что и в t-критерии для независимых выборок. Данные должны содержать группирующую (независимую) переменную, принимающую, по крайней мере, два различных значения (кода), чтобы однозначно определить, к какой группе относится каждое наблюдение в файле данных.
Критерий предполагает, что рассматриваемые переменные являются непрерывными и измерены, по крайней мере, в порядковой шкале.
Критерий серий Вальда-Вольфовица проверяет гипотезу о том, что две независимые выборки извлечены из двух популяций, которые в чем-то существенно различаются между собой, иными словами, различаются не только средними, но также формой распределения. Нулевая гипотеза состоит в том, что обе выборки извлечены из одной и той же популяции, то есть данные однородны.
Рассмотрим алгоритм на основе критерия серий, который предусматривает построение на основании свойств исходного бинарного ряда 
наблюдений, принимающего значения только -1 или 1 по правилу:
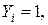если 
если 
где: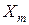 
– медиана исследуемого ряда.
Установлено, что если общее число серий (последовательностей только из подряд идущих 1 или –1)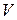 
удовлетворяет условию
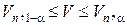
(где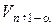 
, 
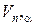- табулированные значения квантилей распределения при заданном критическом уровне значимости 
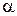и известном объеме наблюдений 
), то гипотеза о стационарности и независимости случайного процесса принимается. В противном случае принимается гипотеза о наличии тренда процесса.
Критерий Колмогорова
Критерий Колмогорова для простой гипотезы является наиболее простым критерием проверки гипотезы о виде закона распределения. Он связывает эмпирическую функцию распределения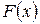 
непрерывной случайной величины 
.
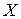Пусть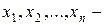 
конкретная выборка из распределения с неизвестной непрерывной функцией распределения 
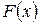и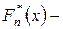 
эмпирическая функция распределения. Выдвигается простая гипотеза 
: 
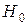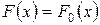(альтернативная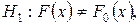 
).
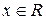Сущность критерия Колмагорова состоит в том, что вводят в рассмотрение функцию
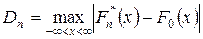
называемой статистикой Колмогорова, представляющей собой максимальное отклонение эмпирической функции распределения 
от гипотетической (т.е. соответствующей теоретической) функции распределения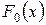 
.
Колмагоров доказал, что при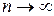 
закон распределения случайной величины 
независимо от вида распределения случайной величины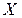 
стремится к закону распределения Колмагорова:
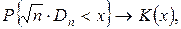
где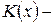 
функция распределения Колмагорова, для которой составлена таблица, ее можно использовать для расчетов уже при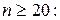 
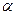
| 0.1 | 0.05 | 0.02 | 0.01 | 0.001 |
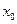
| 1.224 | 1.358 | 1.520 | 1.627 | 1.950 |
Найдем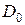 
такое, что 
.
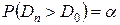Рассмотрим уравнение 
С помощью функции Колмогорова найдем корень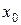 
этого уравнения. Тогда по теореме Колмогорова, 
, 
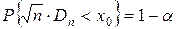, откуда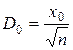 
Если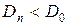 
, то гипотезу 
нет оснований отвергать; в противном случае – ее отвергают.
Оптимальный шаг квантования и длину реализации экспериментальных данных
Квантова́ние — разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование разбиение пространства возможных значений векторной величины на конечное число областей. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.
Однородное (линейное) квантование — разбиение диапазона значений на отрезки равной длины. Его можно представлять как деление исходного значения на постоянную величину (шаг квантования) и взятие целой части от частного: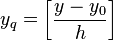 
.
Квантование по уровню — представление величины отсчётов цифровыми сигналами. Для квантования в двоичном коде диапазон напряжения сигнала от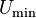 
до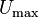 
делится на 
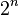интервалов. Величина получившегося интервала (шага квантования):
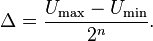
Задание 2. Определение параметров статической модели объекта по выбранной структуре. Анализ построенной модели статической модели
При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным.
Степенная регрессионная модель третьей степени для первого и третьего параметров имеет вид
ЗАДАНИЕ 3. Определение динамических моделей объекта
по данным пассивного эксперимента
Укажем, что множитель z-1=e-pt представляет собой оператор задержки, то есть z-1uk=uk-1, z-2uk=uk-2, и т. д.
Принимая во внимание данное обстоятельство и обозначая моменты дискретного времени тем же символом t, что и непрерывное время (в данном случае t = 0, 1, 2,…), приведем несколько распространенных моделей дискретных объектов для временной области, учитывающих действие шума наблюдения.
ARMAX-модель(AutoRegressive-Moving Average with eXternal input) – модель авторегрессии скользящего среднего):
A(z)y(t)= B(z)u(t-nk)+C(z)e(t),
где nk -величина задержки (запаздывания),
С(z)=1+с1z-1+ с2z-2+…+ сncz-nc
BJ – модель ( Box-Jenkins model) - модель авторегрессии-скользящего среднего, наиболее полно и компактно описывающая автокорреляционные свойства стационарного временного ряда
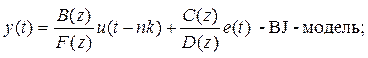
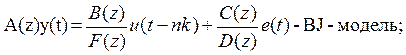
где A(z)=1+a1z-1+a2z-2+…+anaz-na
B(z)=b1+b2z-1+…+ bbn z-nb+1
С(z)=1+с1z-1+ с2z-2+…+ сncz-nc,
D(z)=1+d1z-1+d2z-2+…+dndz-nd,
F(z)=1+f1z-1+ f2z-2+…+ fnfz-nf.