Общие (агрегатные) индексы

Индивидуальные индексы

Способы построения индексов зависят от содержания изучаемых показателей, методологии расчета исходных статистических показателей, имеющихся в распоряжении исследователя статистических данных и целей исследования. По степени охвата статистической совокупности различают индексы индивидуальные и общие (сводные). Каждый индекс включает данные текущего (или отчетного) и базисного уровня.

Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности. Индивидуальный индекс – это результат сравнения двух показателей, относящихся к однородному объекту (например, цене какого – либо товара, объемам его реализации, количеству произведенной продукции в отчетном и базисном периодах т. д.)

Индивидуальные индексы обозначаются буквой I и снабжаются подстрочным знаком индексируемого показателя: так - индивидуальный индекс объема произведенной продукции отдельного вида или количества (объема) проданного товара данного вида, - индивидуальный индекс цен и т.д.

Индивидуальные индексы относятся к одному элементу (явлению) и не требуют суммирования данных. Они представляют собой относительные величины динамики, выполнения обязательств, сравнения. Выбор базы сравнения определяется целью исследования. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком – либо периоде, предшествующем отчетному. При этом возможны два способа расчета индексов – цепной и базисный. Цепные индексы получают сопоставлением текущих уровней с предшествующим, т. е. База сравнения непрерывно меняется. Базисные индексы получают сопоставлением с уровнем периода, принятого за базу сравнения. При территориальных сравнениях за базу принимают данные по какой – либо одной части территории (при региональных сопоставлениях внутри России) или по всей изучаемой территории в целом (международные сопоставления).

При цепном способе расчета за базу отношения принимается индексируемая величина соседнего прошлого периода. В этом случае база расчета в ряду постоянно меняется. При базисном способе расчета за базу принимается индексируемая величина какого – либо одного периода.

Индексы, рассчитанные цепным способом называются цепными, рассчитанные базисным способом – базисными.

Расчет индивидуальных индексов прост, их определяют вычислением отношения двух индексируемых величин.

Для получения индивидуального индекса цен надо цену единицы этого товара в отчетном периоде отнести к цене этого товара в базисном периоде:

где p₁ и p₀ - цена за единицу продукции в текущем и базисном периодах.

Этот индивидуальный индекс показывает, во сколько раз изменилась цена в отчетном периоде по отношению к периоду, с которым проводилось сравнение.

Индивидуальный индекс физического объема продукции рассчитывается по формуле

где q₁ и q₀ - количество продукции данного вида в натуральном выражении в текущем и базисном периодах.

Индивидуальные индексы других показателей строятся аналогично.

С аналитической точки зрения индивидуальные индексы характеризуют изменения индексируемой величины в текущем периоде по сравнению с базисным, т. е. во сколько раз она возросла (уменьшилась) или сколько процентов составляет ее рост (снижение). Значения индексов выражают в коэффициентах или процентах. Если из значения индекса, выраженного в процентах, вычесть 100%, т. е. i - 100, то полученная разность покажет на сколько процентов возросла (уменьшилась) индексируемая величина.

Правило для индивидуальных индексов:

Произведение цепных индексов дает базисный индекс.

Общие (агрегатные) индексы

Общие индексы выражают соотношения сложных социально – экономических явлений, состоящих либо из непосредственно несоизмеримых элементов, либо отдельных частей этих явлений. Общие индексы отражают изменение во всей совокупности элементов сложного явления. Если индексы

охватывают не все элементы, а лишь часть, то их называют групповыми, или субиндексами.

В зависимости от содержания и характера индексируемой величины различают:

· индексы количественных (объемных) показателей, которые характеризуются абсолютными величинами, например, индексы физического объема продукции, работ и услуг, грузооборота, товарооборота;

· индексы качественных показателей, уровень которых дается в форме средних или относительных величин, например, индексы цен, выработки, себестоимости единицы продукции, заработной платы;

Общий, или агрегатный, индекс состоит из:

· индексируемой величины, характер изменения которой определяется;

· соизмерителя, который называется весом.

Методика расчета общих индексов сложнее, чем индивидуальных, и различна в зависимости от характера индексируемых показателей, наличия исходных данных и целей исследования.

Любые общие индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных. Последние в свою очередь делятся на средние арифметические и средние гармонические. Агрегатные индексы качественных показателей могут быть рассчитаны как индексы переменного состава и индексы постоянного (фиксированного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, в индексах постоянного состава – на базе неизменной структуры явлений.

Агрегатный индекс является основной и наиболее распространенной формой индекса, его числитель и знаменатель представляют собой набор – «агрегат» (от латинского – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для целей соизмерения индексируемых величин.

Для исчисления общих индексов необходимо привести их составные части к сопоставимому виду. Например, для оценки изменения объема разнородной продукции в двух сравниваемых периодах надо принять одинаковые цены, а для оценки изменения уровня цен на группу товаров надо сопоставлять одинаковые объемы этих товаров.

Специфика индексного метода состоит в приведении элементов сложного явления (индексируемых величин и весов) к сопоставимому виду. Веса берутся одинаковыми в числителе и знаменателе индекса.

Типичным индексом количественных показателей является индексфизического объема продукции. Сложность при построении этого индекса заключается в том, что объемы разных видов продукции и товаров в натуральном выражении несоизмеримы и непосредственно суммироваться не могут. Нельзя, например, складывать килограммы хлеба с литрами молока, метрами ткани и парами обуви. Экономически бессмысленно непосредственно суммировать килограммы мяса и рыбы, так как полученный результат в прямом смысле не являлся бы «ни рыбой, ни мясом». Причиной несоизмеримости здесь является неоднородность – различие натуральной формы и свойств.

Коэффициенты соизмерения обеспечивают количественную сравнимость, позволяют учитывать «вес» продукта в реальном экономическом процессе. Поэтому их показатели-сомножители, связанные с индексируемыми величинами, принято называть весами индексов, а умножение на них – взвешиванием.

Умножая количество произведенной продукции на цены (которые, как правило, выступают в качестве соизмерителя неоднородной продукции), получаем стоимостное выражение продукции каждого вида, которое допускает суммирование.

Стоимость продукции представляет собой произведение количества продукции в натуральном выражении на цену единицы продукции.

Отношение стоимости продукции текущего периода в текущих ценах

к стоимости продукции базисного периода в базисных ценах представляет собой агрегатный индекс стоимости продукции или товарооборота.

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции.

Если из значения индекса стоимости вычесть 100%, то разность покажет на сколько процентов возросла (уменьшилась) стоимость продукции в отчетном периоде по сравнению с базисным.

С помощью агрегатных индексов можно рассчитать не только относительное изменение изучаемого явления, но и разложить абсолютный прирост результативного показателя.

Разность числителя и знаменателя формулы показывает на сколько денежных единиц (рублей) увеличилась (уменьшилась) стоимость продукции (товарооборота) в текущем периоде по сравнению с базисным.

Значение индекса стоимости продукции (товарооборота) зависит от двух факторов: изменения количества продукции (объемов) и цен.

Для того чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить в формуле влияние другого фактора, зафиксировав его как в числителе, так и в знаменателе на уровне одного и того же периода. Так, если продукцию сравниваемых периодов оценивать по одним и тем же, например, базисным ценах, то такой индекс отразит изменение только одного фактора – индексируемого показателя и будет представлять собой агрегатный индекс физического продукции:

где q₁ и q₀ - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p₀ - цена единицы продукции (отдельного вида) в базисном периоде.

Индекс физического объема продукции показывает, во сколько раз увеличился (уменьшился) физический объем продукции или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.

В числителе формулы – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде.

Если из значения индекса физического объема продукции вычесть 100%, то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным из-за роста (снижения) объема ее производства.

Абсолютное изменение физического объема продукции вычисляется как разность между числителем и знаменателем формулы.

Экономически эта разность показывает, на сколько денежных единиц (рублей) изменилась стоимость продукции в результате роста (уменьшения) ее физического (т. е. натурального) объема, т. е. количества проданных товаров. Изменение цен на продукцию в текущем периоде по сравнению с базисным не влияет на изменение индекса.

Обычно при построении агрегатного индекса физического объема продукции в качестве соизмерителей принимаются сопоставимые, фиксированные цены на уровне базисного периода, что позволяет устранить влияние изменения цен на динамику объема (количества) продукции.

Использование неизменных цен в зависимости от объекта исследования дает возможность изучить динамику выпуска совокупности произведенных товаров на отдельном предприятии, в отраслях промышленности и промышленности в целом. Если объектом исследования является какой – то регион, то индекс рассчитывается по товарам, произведенным предприятиями региона.

Сопоставимые цены не должны сильно отличаться от действующих (текущих) цен. Поэтому их периодически пересматривают, переходят к новым сопоставимым ценам.

В период перехода к рыночной экономике в условиях высокой инфляции в качестве сопоставимых цен часто используются цены предшествующего периода, с которым происходит сравнение.

Рассмотрим принципы построения агрегатных индексов качественных показателей на примере индекса цен.

Поскольку этот индекс характеризует изменение цен, индексируемой величиной в нем будет цена товара. Влияние количества проданных товаров должно быть устранено, а это возможно только в том случае, если количество продаваемых товаров неизменно в оба периода, т. е. количество товаров одного из периодов принято в качестве весов индекса.

При построении индекса цен в качестве весов индекса обычно берут количество товаров, проданных в текущем (отчетном) периоде. Это объясняется тем, что такое исчисление индекса цен позволяет определить не только относительное изменение цен (путем деления числителя индекса

на его знаменатель, но и абсолютную экономию (-) или абсолютный перерасход (+) денежных средств покупателей в результате изменения цен на эти товары (как разность между числителем и знаменателем индекса).

Агрегатный индекс цен с отчетными весами впервые предложен в 1874 г. немецким экономистом Г. Пааше и носит его имя.

Формула агрегатного индекса цен Пааше:

где числитель формулы - фактическая стоимость продукции (товарооборот) отчетного периода;

знаменатель формулы - условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.

Индекс цен Пааше показывает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.

Если из индекса цен вычесть 100%, то разность покажет на сколько процентов в среднем возрос (уменьшился) за это время уровень цен на массу товаров, реализованную в отчетном периоде.

При таком методе, рассчитав индекс цен по формуле, можно подсчитать экономический эффект от изменения цен.

Более правильно отразит изменение цен индекс, построенный по продукции базисного периода (предложен в 1864 г. немецким экономистом Э. Ласпейресом и носит его имя).

Формула агрегатного индекса цен Ласпейреса:

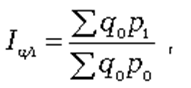
Значения индексов цен Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание.

Индекс Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде, и фактическую экономию (перерасход) от изменения цен, т. е. индекс цен Пааше показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.

Экономическое содержание индекса Ласпейреса другое: он показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию (перерасход), которую можно было бы получить от изменения цен, т. е. условную экономию (перерасход). Иначе говоря, индекс Ласпейреса показывает во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде. Поэтому применение формулы Ласпейреса ограничено особыми условиями исследования (например, при прогнозировании объемами товарооборота, в связи с намечаемыми изменениями цен на товары в предыдущем периоде).

«Идеальный» индекс цен Фишера (по имени американского экономиста И,Фишера) представляет собой среднюю геометрическую из произведения двух агрегатных индексов цен Ласперейса и Пааше.

Идеальность формулы заключается в том, что индекс является обратимым во времени, т.е. при перестановке базисного и отчетного периодов полученный «обратный» индекс – это величина обратная величине первоначального индекса.

Однако геометрическая форма индекса имеет принципиальный недостаток: она лишена конкретного экономического содержания.

Индекс Фишера в силу сложности расчета и трудности экономической интерпритации на практике используется довольно редко, чаще всего – при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения.

Рассмотрев индекс цен, аналогично рассуждаем и при построении всех других индексов качественных показателей.

Рассмотрение методологии исчисления индексов и их применение в экономическом анализе позволяет сделать следующее обобщение.

Индивидуальные индексы являются обычными относительными величинами сравнения, т. е. могут быть названы индексами только в широком понимании этого термина.

Важной особенностью общих индексов, построение и расчет которых составляют суть индексного метода, является то, что они обладают синтетическими и аналитическими свойствами:

Синтетические свойства общих индексов состоят в том, что они выражают относительные изменения сложных (разнотоварных) явлений, отдельные части и элементы которых непосредственно несоизмеримы.

Аналитические свойства общих индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.

Таким образом, общие индексы являются синтетическими и аналитическими показателями, играющими важную роль в социально-экономических исследованиях.

 

4. Расчет средних арифметических и гармонических индексов Часто вместо абсолютных значений индексируемых показателей могут быть известны не абсолютное, а относительное изменение физического объема реализации и, к тому же, товарооборот предшествующего периода. В тех случаях, когда не известны достаточные данные для расчета сводных индексов, формулы для соответствующих индексов могут быть модифицированы с целью осуществления расчетов заданных показателей по имеющейся информации. Например, сводный (агрегатный) индекс может быть преобразован в средний арифметический и средний гармонический индексы. Агрегатный способ исчисления общих индексов в статистике является основным наиболее распространенным, вместе с тем применяется и другой способ расчета общих индексов как средних из соответствующих индивидуальных индексов. К исчислению таких средневзвешенных индексов прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если неизвестны количества произведенных отдельных видов продукции в натуральных измерителях, но известны индивидуальные индексы и стоимость продукции базисного периода, можно определить средний арифметический индекс физического объема продукции. Исходной базой построения средневзвешенного индекса физического объема продукции служит его агрегатная форма. Из имеющихся данных агрегатной формы индекса непосредственно можно только получить знаменатель формулы. Для нахождения числителя используем формулу индивидуального индекса объема продукции. Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами служит стоимость отдельных видов продукции в базисном периоде: где iq - индивидуальный индекс по каждому виду продукции; q0 p0 - стоимость продукции каждого вида в базисном периоде. Средний взвешенный гармонический индекс физического объема продукции где q1 p1 - стоимость продукции каждого вида в текущем периоде. Любой агрегатный индекс может быть представлен как взвешенная величина из индивидуальных индексов найдем . Подставим в общий индекс цены , тогда получимсреднегармонический взвешенный индекс 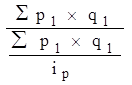. Если известны индивидуальные индексы цен по отдельным видам продукции и стоимость отдельных видов продукции, то применяются средние взвешенные индексы цен (средний взвешенный арифметический и средний взвешенный гармонический индексы цен). Формула среднего взвешенного арифметического индекса цен где i - индивидуальный индекс по каждому виду продукции; p0 q0 - стоимость продукции каждого вида в базисном периоде. Формула среднего взвешенного гармонического индекса цен где p1 q1 - стоимость продукции каждого вида в текущем периоде. Использование исходной формы агрегатного индекса или среднегармонического, средневзвешенного индекса зависит от исходных данных, имеющихся в распоряжении исследователя.

5. Индексы переменного, фиксированного (постоянного) состава и структурных сдвигов

При динамическом анализе средних показателей используют систему индексов, состоящих из индекса переменного состава, индекса фиксированного (постоянного) состава и индекса структурных сдвигов. Данная система индексов позволяет решить задачу изменения структуры от изменения качественных показателей, а также позволяет выявить влияние факторов на индексируемую величину. Система индексов используется, когда соизмеримая продукция производится на разных участках. Индекс переменного состава – это относительная величина, характеризующая динамику двух средних показателей для однородных совокупностей. Этот индекс отражает влияние двух факторов: – изменение индексируемого показателя у отдельных объектов (частей целого); – изменение удельного веса этих частей в общей структуре совокупностей.   Индекс переменного состава показывает изменение среднего значения качественного показателя (средней цены) в текущем периоде по сравнению с базисным или предыдущим. Индекс фиксированного состава – характеризует динамику двух средних величин при одинаковой фиксированной структуре совокупности в отчетном периоде. Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилась средняя величина показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т.е. когда влияние структурного фактора устранено.Сводный индекс фиксированного (постоянного) состава характеризует изменение величины качественного показателя в среднем по отдельным объектам совокупности. Например, изменение общей средней цены за счет изменения индивидуальных цен в отчетном периоде по сравнению с базисным: Индекс постоянного состава показывает изменение среднего значения качественного показателя (средней цены) в зависимости от изменения этого показателя у отдельных единиц совокупности. Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов, как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру, к фактической средней этого показателя в базисном периоде. Индекс структурных сдвигов – это отношение двух средних величин, рассчитанных для разной структуры совокупности, но при постоянной величине индексируемого показателя в базисном периоде.показателя за счет изменения структуры количественного показателя: физического объема продукции (ассортимента продукции). Положительным показателем индекса структурных сдвигов является величина, равная или больше Индекс структурных сдвигов показывает изменение средней величины анализируемого качественного единицы (1). 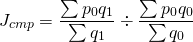Например, изменение средней цены в отчетном периоде за счет изменения физического объема: Индекс структурных сдвигов показывает изменение среднего значения качественного показателя в зависимости от изменения структурных пропорций. Между индексами переменного, фиксированного состава существует взаимосвязь. Индекс переменного состава всегда будет равен произведению индексов фиксированного состава и структурных сдвигов Jпс = Jфс x Jсс.