Применение тех или иных методов расчета напорных трубопроводов обусловлено конструктивными характеристиками и назначением трубопровода.
При расчете простого трубопровода находится расчетная зависимость из уравнения Бернулли и уравнения расхода, а также из формулы для учета потерь по длине и на местных сопротивлениях.
Рассмотрим две основные расчетные схемы: истечение в атмосферу и истечение под уровень.
Схема истечения в атмосферу показана на рис. 2.
      |
Рис. 2
Напишем уравнение Бернулли для сечений 1–1 и 2–2:
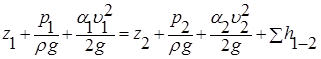 , (19)
, (19)
| где z 1 – z 2 = | H; |

| 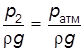 ; ;
|
| a1 » | a2 = 1; |
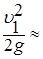
| 0. |
Тогда
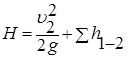 , (20)
, (20)
где 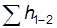 – –
| сумма потерь по длине и местных сопротивлений; |
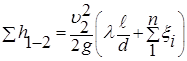 .
.
Подставляя последнее выражение в (20), получим зависимость:
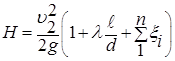 . (21)
. (21)
Схема истечения под уровень показана на рис. 3.




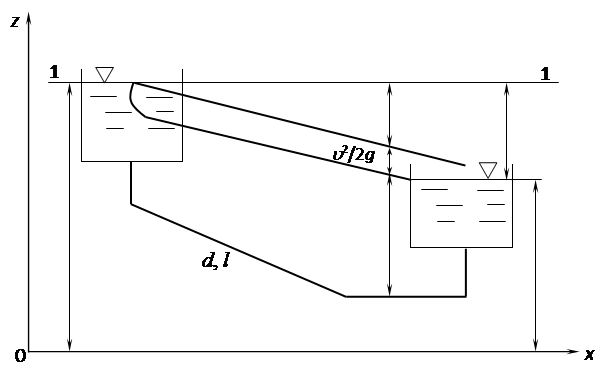
Рис. 3
Напишем уравнение Бернулли для сечений 1–1 и 2–2:
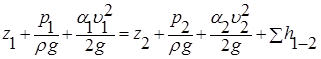 , (22)
, (22)
| где z 1 – z 2 = | H; |

| 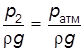
|
| a1 » | a2 = a = 1; |
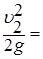
|  0; 0;
|
тогда
 , (23)
, (23)
где 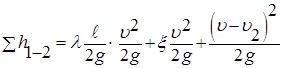 (24)
(24)
В выражении (24) два последних члена представляют собой потери на местных сопротивлениях, причем последнее слагаемое определяет потери напора при внезапном расширении и вычисляется по теореме Борда.
Решая совместно уравнения (23) и (24) и учитывая, что  , получим
, получим
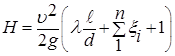 . (25)
. (25)
Сопоставляя уравнения (21 и 25), можно видеть, что по форме написания они совершенно тождественны.
Различие между уравнениями по физическому смыслу заключается лишь в том, что единица, стоящая в скобках правой части уравнения (21), относится к скоростному напору на выходе потока из трубы в атмосферу.
Следовательно, единица определяет кинетическую энергию, которую поток уносит с собой и которая может быть в дальнейшем использована для совершения работы.
При истечении под уровень единица в скобках в уравнении (25) определяет собой потерянный напор на внезапное расширение при входе потока из трубы в резервуар.
|
|
Следовательно, при истечении под уровень вся энергия, которой располагает поток, расходуется только на преодоление сопротивлений.
При расчете простого трубопровода решаются три основные задачи:
Первая задача. Требуется определить необходимый действующий напор H для трубопровода длиной l, м, диаметром d, м, для пропуска расхода Q.
Решение сводится к прямому вычислению напора по формуле (21).
Коэффициенты l и x могут быть связаны с числом Рейнольдса
 ,
,
где Q и d заданы по условию задачи.
Вторая задача. Требуется определить расход Q при заданных H, l и d.
Расход определяется из уравнения расхода 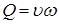 и выражения (21). При совместном решении получаем формулу для вычисления расхода:
и выражения (21). При совместном решении получаем формулу для вычисления расхода:
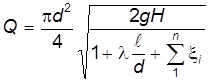 . (26)
. (26)
 Для определения l и x необходимо знать скорость v или искомый расход
Для определения l и x необходимо знать скорость v или искомый расход 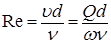 , поэтому Q можно найти по формуле (26) методом попыток или графоаналитическим способом, путем использования формулы (21) и построения графика
, поэтому Q можно найти по формуле (26) методом попыток или графоаналитическим способом, путем использования формулы (21) и построения графика 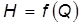 (рис. 4).
(рис. 4).
Рис. 4
Задаваясь значениями  , по формуле
, по формуле
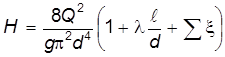
вычисляем ряд значений 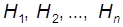 .
.
Третья задача. Требуется определить диаметр трубопровода d по заданным H, Q, и l.
Диаметр трубопровода d определяется графоаналитическим способом. Строится кривая  : задаваясь рядом значений
: задаваясь рядом значений 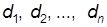 , вычисляем
, вычисляем 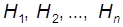 (рис. 5). При этом для каждой точки графика вычисление
(рис. 5). При этом для каждой точки графика вычисление 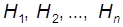 , проводится, без подбора, так как при каждом
, проводится, без подбора, так как при каждом 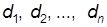 число Рейнольдса вычисляется непосредственно по формуле
число Рейнольдса вычисляется непосредственно по формуле 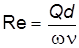 .
.

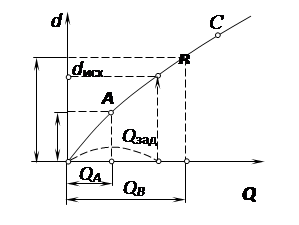
Рис. 5
Замечание 1. Для длинных трубопроводов, когда потерями на местных сопротивлениях можно пренебречь, все три основные задачи решаются на основе использования формулы
|
|
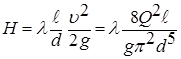 . (27)
. (27)
Следовательно, методика расчета сохраняется, но расчёты значительно упрощаются.
Замечание 2. При квадратичном законе сопротивления, т.е. когда l, а также коэффициент Шези С не зависят от Re, расчёт можно выполнить по формуле
 . (28)
. (28)
Первые две задачи сводятся к прямому вычислению их по формуле (28), причём К определяется по таблицам по заданному диаметру d.
Для решения третьей задачи (определить d по данным H, Q и l) сначала вычисляется по формуле (28) необходимое значение К, по которому затем из таблиц находится ближайшее большее и ближайшее меньшее значения 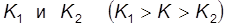 , и по технико-экономическим условиям принимается d.
, и по технико-экономическим условиям принимается d.