Представление о сопротивлении, индуктивности и емкости как идеализированных элементах электрической цепи основано на предположении, что потери энергии, магнитное поле и электрическое поле сосредотачиваются в отдельных, не зависящих друг от друга элементах цепи. Раздельное рассмотрение сопротивления, индуктивности и емкости представляет приближенный метод исследования цепи. В действительности потери энергии, магнитные и электрические поля сопутствуют друг другу.
Электропроводность всякого изотропного вещества характеризуется так называемой удельной электрической проводимостью, равной отношению величины плотности тока проводимости к величине напряженности электрического поля. Величина, обратная удельной электрической проводимости, называется удельным электрическим сопротивлением.
Электрическое сопротивление проводника при постоянном токе, равное отношению постоянного напряжения на рассматриваемом проводнике к постоянному току в нем, зависит от длины проводника l (м), площади поперечного сечения S (м 2) и удельного сопротивления r (Ом×м)
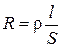 , Ом.
, Ом.
В широких пределах изменения температуры зависимость удельного сопротивления проводника от температуры практически прямолинейна, причем в случае металлических проводников кривая ρ= f (q) с повышением температуры возрастает, а в случае неметаллических материалов (например, угля) и электролитов - падает.
Если обозначить через ρ1 и ρ2 удельные сопротивления при температурах q1и q2, а через q0- температуру, соответствующую точке пересечения спрямленной характеристики r= f (q) с осью (рисунок 1.9), то получится пропорция
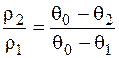 .
.
Эта пропорция служит для вычисления ρ2, если известно ρ1.

Значения r1(q1 = 20 °С) и q0для некоторых проводников приведены ниже:
| алюминий | r1= 2,83×10-8Ом м; | q0= -236 °С; |
| медь | r1= 1,724×10-8Ом∙ м; | q0= -234 °С; |
| уголь | r1= 3500 Ом∙ м; | q0= +1825 °С. |
Как было пояснено выше, понятие сопротивления непосредственно связано с потерей энергии, т.е. c необратимым процессом поглощения электромагнитной энергии.
Количество тепла, выделяемого при прохождении тока через какой либо проводник, зависит от целого ряда факторов, в том числе от частоты тока. При невысоких частотах сопротивление проводника мало отличается от сопротивления при постоянном токе. С повышением же частоты ток распределяется по сечению проводника неравномерно: внутри проводника плотность тока уменьшается, ток вытесняется к поверхности проводника, что вызывает как бы уменьшение сечения проводника, а значит увеличение сопротивления. Последнее приводит к увеличению тепловых потерь в проводнике. Это явление носит название поверхностного эффекта.
Неравномерность распределения тока по сечению проводника и возрастание вследствие этого тепловых потерь происходят также под влиянием тока, проходящего по соседнему проводнику. Это явление носит название эффекта близости.
Кроме того, переменное магнитное поле наводит в окружающей проводник проводящей среде вихревые токи, что вызывает дополнительную потерю энергии на нагрев.
К этому можно еще добавить излучение в пространство электромагнитной энергии, наблюдаемое при высоких частотах и вызывающее дополнительное увеличение сопротивления.
Вследствие наличия магнитного и электрического полей проводник наряду с сопротивлением имеет некоторую индуктивность и емкость.
Вычисление сопротивления, индуктивности и емкости проводника с учетом указанных выше факторов относится к задачам теории поля.
Теперь представим себе простейшую индуктивную катушку в виде нескольких круговых витков проводника, по которому проходит ток.
При постоянном токе напряжение на зажимах катушки определится величиной падения напряжения на ее сопротивлении в соответствии с (1.1), и ток во всех точках витков будет одинаковым.
При переменном же токе изменяющееся магнитное поле будет наводить в витке ЭДС самоиндукции. Между витками, так же как и между отдельными точками смежных витков, электрическое поле станет переменным. В связи с этим ток в различных витках будет неодинаковым, так как появится ток смещения между витками. Чем выше частота переменного тока, тем больше будут ЭДС самоиндукции и ток смещения. При низких частотах током смещения можно пренебречь; при высоких же частотах ток смещения, обусловленный изменением напряженности электрического поля, может быть соизмерим по величине с током в витках или даже может превышать его. Таким образом, в зависимости от выбранного диапазона частот индуктивная катушка может быть представлена либо как сопротивление R (при постоянном токе - рисунок 1.10, а), либо как индуктивность L с последовательно включенным сопротивлением R (при низких частотах - рисунок 1.10, б), либо как индуктивность L и сопротивление R, соединенные параллельно с емкостью С (при высоких частотах - рисунок 1.10, в).

Если катушка имеет много витков, то проходящий через нее ток создает магнитный поток, пропорциональный числу витков. Считая, что этот магнитный поток сцеплен со всеми витками катушки, приходим к выводу, что потокосцепление самоиндукции и соответственно индуктивность катушки пропорциональны квадрату числа витков.
Положим, например, что катушка, состоящая из w витков, насажена на тороид или достаточно длинный прямолинейный сердечник, длина которого l (м) и площадь поперечного сечения S (м 2).
Обозначим через m a абсолютную магнитную проницаемость сердечника (равную произведению относительной магнитной проницаемости m на магнитную постоянную m0= 4p·10-7 Гн/м). Абсолютная магнитная проницаемость для изотропного вещества – скалярная величина, характеризующая магнитные свойства вещества; она равна отношению величины магнитной индукции к величине напряженности магнитного поля.
Магнитный поток в сердечнике определяется отношением намагничивающей силы (н.с.) всей катушки iw к магнитному сопротивлению магнитопровода 
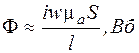 .
.
Поэтому индуктивность катушки согласно определению
 , Гн.
, Гн.
Она определяется геометрическими размерами катушки, магнитной проницаемостью сердечника и квадратом числа витков.
Перейдем теперь к рассмотрению плоского конденсатора, состоящего из двух параллельных пластин, разделенных диэлектриком.
При постоянном напряжении и идеальном диэлектрике тока в цепи не будет. Если напряжение переменно, то в процессе изменения электрического заряда возникает переменный ток, создающий переменное магнитное поле. Эффект, вызываемый магнитным полем, может быть учтен в электрической схеме замещения с помощью некоторой индуктивности, включенной последовательно с емкостью конденсатора. Обычно этой индуктивностью пренебрегают из-за ее относительной малости. Наконец, в диэлектрике благодаря некоторой проводимости возникают тепловые потери, которые возрастают с частотой. Потери на нагрев учитываются в схеме замещения конденсатора посредством сопротивления R, включенного параллельно емкости С (рисунок 1.11).
Емкость конденсатора определяется размерами пластин, расстоянием между ними и диэлектрическими свойствами среды, заполняющей пространство между пластинами.

Если расстояние между пластинами конденсатора (толщина диэлектрика) достаточно мало по сравнению с размерами пластин, то емкость конденсатора вычисляется по формуле
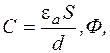
где e а - абсолютная диэлектрическая проницаемость изоляции между пластинами (равная произведению относительной диэлектрической проницаемости e на электрическую постоянную e0= 8,855∙10-12 Ф/м);
S - площадь поверхности каждой пластины, м 2;
d – расстояние между пластинами, м.
Абсолютная диэлектрическая проницаемость для изотропного вещества — скалярная величина, характеризующая электрические свойства диэлектрика; она равна отношению величины электрического смещения к величине напряженности электрического поля.
Чем выше частота и чем больше линейные размеры самих устройств, тем в большей мере проявляется взаимосвязь электрических и магнитных параметров и неотделимость друг от друга электрического и магнитного полей, являющихся лишь двумя сторонами единого электромагнитного поля.
Строго разграничить области частот, при которых справедлива та или иная схема замещения, не представляется возможным, так как это зависит от множества факторов.