1. ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ И УГЛА ПОПОЛАМ
Деление отрезка пополам (рис.1). Отрезок АВ прямой m делится на две равные части перпендикуляром n, проведенным через точки пересечения С и D дуг окружностей радиуса R>0,5АВ с центрами соответственно в точках А и В.
Точка Е – середина отрезка АВ.
Деление угла пополам (рис.2). Из вершины заданного угла провести дугу произвольного радиуса R до пересечения со сторонами угла в точках А и В. Из полученных точек как из центров провести две дуги равных радиусов до их взаимного пересечения в точке M. Биссектриса ОМ делит заданный угол пополам.

Рис.1 Рис.2
2. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
Деление окружности на три, шесть и двенадцать частей (рис.3). Провести две взаимно перпендикулярные оси АВ и СD и начертить окружность радиуса R. Из любой точки конца диаметра (например А) провести радиусом R дугу до пересечения с окружностью в точках 1 и 2. Отрезок 1–2 – искомая сторона правильно вписанного треугольника 1В2. В свою очередь, отрезки А1=А2 и С1=D2 соответственно равны сторонам правильных вписанных шестиугольника и двенадцатиугольника. Для построения недостающих точек (вершин углов) достаточно провести из точки В противоположного конца диаметра окружности дугу того же радиуса R до пересечения с окружностью или измерителем последовательно отложить соответствующие отрезки на основной окружности.
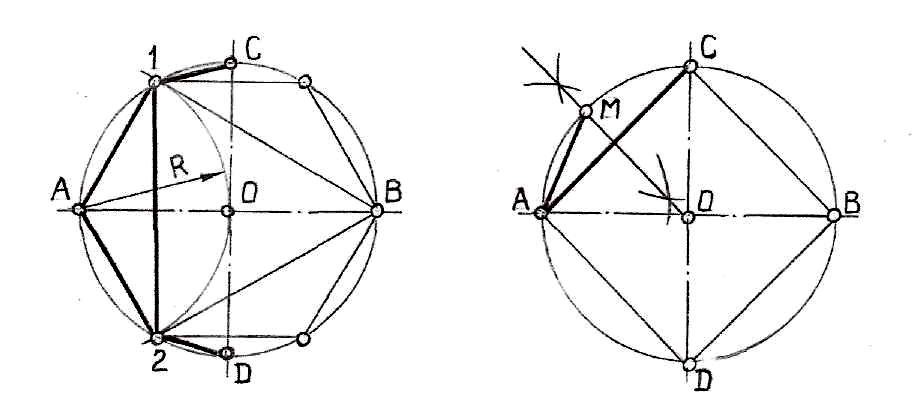
Рис.3 Рис.4
Деление окружности на четыре и восемь частей (рис.4). Провести две взаимно перпендикулярные оси АВ и CD, начертить окружность радиуса R. Отрезки АС=СВ=ВD, соединяющие концы диаметров, являются искомыми сторонами правильного четырехугольника, вписанного в окружность.
Для деления окружности на восемь частей построить из центра О перпендикуляр к одной из сторон (например АС) и продолжить его до пересечения с окружностью в точке М. Отрезок АМ – искомая сторона правильного восьмиугольника, вписанного в окружность.
Деление окружности на пять и десять частей (рис.5). Провести два взаимно перпендикулярные оси АВ и СD, начертить окружность радиуса R. Разделить радиус ОВ пополам в точке М. Из точки М, как из центра, провести дугу радиусом МС до пересечения её с диаметром АВ в точке К. Отрезок СК равен стороне правильного вписанного пятиугольника, отрезок ОК – десятиугольника. Для деления окружности на пять частей достаточно дугой радиуса СК сделать засечки на исходной окружности в точке 1, 2 и далее; используя точки 1 и 2 как центры, тем же радиусом отметить точки 3 и 4. Точки С, 1, 3, 4, 2 – вершины правильного вписанного пятиугольника.

Рис.5 Рис.6
Деление окружности на семь частей (рис.6). Провести две взаимно перпендикулярные оси, начертить окружность радиуса R. Из точек А и В концов горизонтального диаметра АВ провести дуги окружности радиусом R=АО=ВО и отметить точки их пересечения 1 и 2 с исходной окружностью. На пересечении хорды 1-2 с радиусом ОD отметить точку М. Отрезок ОМ равен стороне правильного вписанного семиугольника. Для его построения последовательно, начиная с точки D, отметить на исходной окружности точки 3, 4, 5, 6, 7, 8 радиусом R=ОМ.
ОФОРМЛЕНИЕ РАБОТЫ:
1. Деление отрезка на части
ПОСТРОЕНИЕ
2. Деление углов на две части
ПОСРОЕНИЕ и т.д.