Переменный ток – ток, амплитуда и направление кот. изменяются во времени.
Ток i(t) называют мгновенным.
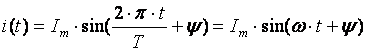
Принято среднее значение функции времени определять за период
Действующим значением синусоидальной функции называется ее среднеквадратичное значение за период
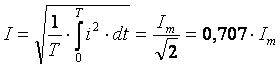
Анализ цепей с последовательным соединением элементов и их решение. Активное, реактивное и полное сопротивление ветви.
Электрическая цепь с последовательным соединением элементов R, L и C
|
Пусть в заданной схеме с последовательным соединением элементов R, L и C (рис. 47) протекает переменный ток
.
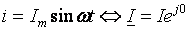По 2-му закону Кирхгофа для мгновенных значений функций получим уравнение в дифференциальной форме:
.
То же уравнение в комплексной форме получит вид: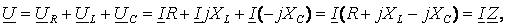 
где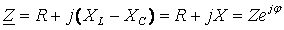 
комплексное сопротивление, 
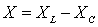реактивное (эквивалентное) сопротивление, 
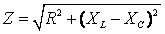модуль комплексного или полное сопротивление, 
аргумент комплексного сопротивления или угол сдвига фаз между напряжением и током на входе схемы. При 
фазный угол φ>0, при этом цепь в целом носит активно-индуктивный характер, а при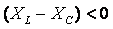 
и φ<0 – цепь в целом носит активно-емкостный характер.
Уравнение закона Ома для последовательной схемы будет иметь вид:
в комплексной форме,
в обычной форме для модулей.
|
Векторная диаграмма тока и напряжений при φ>0 показана на рис. 48.
В рассматриваемой цепи на переменном токе будут происходить одновременно два физических процесса: преобразование энергии в другие виды в резисторе R (активный процесс) и взаимный обмен энергией между магнитным полем катушки, электрическим полем конденсатора и источником энергии (реактивный процесс).
Анализ цепей с параллельным соединением элементов и их решение.
|
Пусть на входе схемы рис. 49 действует переменное напряжение:
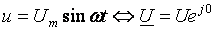
По 1-му закону Кирхгофа для мгновенных значений функций получаем уравнение в дифференциальной форме:
То же уравнение в комплексной форме получит вид:
,
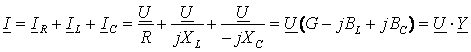где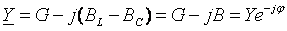 
комплексная проводимость, 
активная проводимость, 
реактивная индуктивная проводимость, 
реактивная емкостная проводимость, 
реактивная (эквивалентная) проводимость, 
модуль комплексной проводимости или полная проводимость,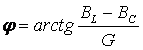 
аргумент комплексной проводимости или угол сдвига фаз между напряжением и током на входе схемы. При 
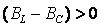и φ>0 – цепь в целом носит активно-индуктивный характер, а при 
и φ<0 – цепь в целом носит активно-емкостный характер.
Уравнение закона Ома для параллельной схемы будет иметь вид:
в комплексной форме;
в обычной форме для модулей.
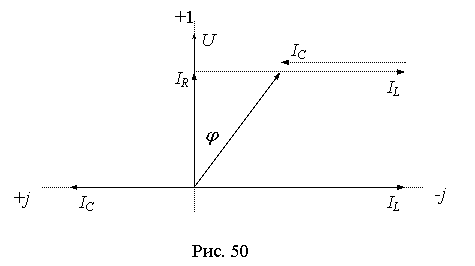
Векторная диаграмма токов и напряжения при φ>0 показана на рис. 50.
|
На переменном токе в рассматриваемой цепи будут происходить одновременно два физических процесса: преобразование электрической энергии в другие виды (активный процесс) и взаимный обмен энергией между магнитным полем катушки, электрическим полем конденсатора и источником энергии (реактивный процесс).