Гармонические колебания (2 часа)

 

План занятия

Колебательное движение. Качественное рассмотрение.

Дифференциальное уравнение гармонических колебаний. Частота, период, амплитуда, фаза.

Пружинный маятник. Математический маятник.

Закон сохранения энергии для колебательных систем.

 

Задачи

1.6.1. Во сколько раз время прохождения первой половины амплитуды меньше времени прохождения второй половины? В начальный момент времени колеблющееся тело находится в положении равновесия и имеет некоторую скорость.

1.6.2. Через какую долю периода скорость колеблющегося тела уменьшается от максимальной до одной трети максимальной?

1.6.3. Математический маятник длиной в начальный момент времени отклонили на малый угол от положения равновесия и отпустили без начальной скорости. Через какое минимальное время маятник будет отклонен от положения равновесия на угол ?

1.6.4. На груз массой , висящий на пружине с жесткостью , положили перегрузок массой 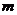. В начальный момент грузы находились в положении равновесия. Затем грузам сообщили скорость 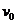, направленную вертикально вниз. Найти максимальную силу, действующую на груз со стороны перегрузка 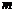в течение последующего движения. В процессе движения перегрузок от груза не отрывается. Найти моменты времени, в которые эта сила будет максимальна.

1.6.5. К свободному концу вертикальной невесомой недеформированной пружины, прикрепленной к потолку, подвешивают груз, который затем отпускают без начальной скорости. Амплитуда колебаний см. Определить максимальную величину скорости груза.

1.6.6. Груз массой 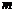прикреплен к пружине с коэффициентом жесткости , подвешенной к горизонтальному потолку. Доказать, что частота колебаний груза совпадает с частотой его колебаний на гладкой горизонтальной поверхности под действием той же пружины, расположенной горизонтально.

1.6.7. Невесомый стержень длиной шарнирно подвешен за конец к потолку. На втором конце стержня и в точке, находящейся на расстоянии от закрепленного конца, укреплены две точечных массы 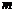и соответственно. Найти период малых колебаний стержня.

1.6.8*. К горизонтально расположенной пружине с жесткостью 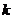привязано тело массой 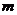, находящееся на шероховатой горизонтальной поверхности. Коэффициент трения между телом и поверхностью . В начальный момент времени тело находится в положении, в котором пружина не деформирована. Затем телу толчком сообщают скорость 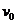. Через какое минимальное время после начала движения тело в первый раз остановится? Будет ли оно двигаться дальше и если да, то через какое время остановится во второй раз?

1.6.9*. Доска длиной , движущаяся по гладкой горизонтальной поверхности со скоростью 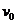, наезжает на шероховатую поверхность. Скорость доски перпендикулярна границе раздела между поверхностями. Коэффициент трения между доской и шероховатой поверхностью равен . Известно, что через некоторое время вся доска оказывается на шероховатой поверхности. Через какое время на ней окажется половина доски?

Домашнее задание

1. Груз массой 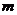, находящийся на гладкой горизонтальной поверхности, прикреплен к горизонтальной пружине с коэффициентом жесткости . Второй конец пружины закреплен. В начальный момент пружину растянули на величину , а грузу толчком сообщили начальную скорость 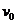, направленную к положению равновесия груза. Через какое минимальное время после начала движения скорость груза будет максимальной?

2. Математический маятник длиной 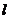в начальный момент времени отклонили на малый угол и сообщили маятнику скорость 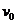, направленную от положения равновесия. Считая, что маятник будет совершать гармонические колебания, найти, через какое минимальное время маятник будет отклонен от положения равновесия на максимальный угол.

3. Груз массой 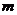, находящийся на гладкой горизонтальной поверхности, прикреплен к горизонтальной пружине с коэффициентом жесткости . Второй конец пружины закреплен. В начальный момент пружину растянули на величину , а грузу толчком сообщили начальную скорость 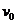, направленную от положения равновесия груза. Найти амплитуду колебаний груза?

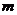4. Муфта массой может двигаться без трения вдоль гладкой горизонтальной штанги. Муфта соединена с концами штанги пружинами с коэффициентами жесткости и , длина каждой из которых в недеформированном равна длине штанги. Найти частоту колебаний муфты. Найти амплитуду колебаний, если вначале муфту удерживали посередине штанги, а затем без толчка отпустили.

5*. По хорде некоторой планеты сделана гладкая шахта. В шахту без начальной скорости опускают тело. Через какое время тело окажется на ближайшем расстоянии к центру планеты? Ускорение силы тяжести на поверхности планеты . Все необходимые размеры считать известными.

 

 

Гидростатика (2 часа)

 

План занятия

Отличие жидкостей от твердых тел. Давление. Закон Паскаля. Невекторный характер давления. Гидростатическое давление. Закон Архимеда. Плавание тел.

Задачи

1.7.1. В жидкость целиком погружено тело, имеющее форму параллелепипеда, две грани которого параллельны поверхности жидкости. Найти равнодействующую всех сил, действующих на тело со стороны жидкости.

1.7.2. Плоская грань сосуда с водой наклонена под углом к горизонту. В грань вбит гвоздь, к которому привязана тонкая невесомая нить. К нити привязан шар объемом 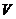. Плотность вещества шара больше плотности воды. Найти силу натяжения нити. Плотность воды .

1.7.3. В сосуде с водой плавает тело. Найти давление воды около дна сосуда. Высота столба воды в сосуде (вместе с телом) равна .

1.7.4. На поверхности воды плавает льдинка. Как изменится уровень воды, если льдинка растает?

1.7.5. В цилиндрическом сосуде с водой площадью сечения $S$ плавает лед с вмороженным в него куском свинца. Масса куска свинца 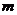, плотность свинца . Понизится уровень воды в сосуде или повысится, если лед растает? На сколько? Плотность воды .

1.7.6*. В сосуде на поверхности воды находятся в равновесии 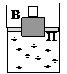подвижные поршень П и втулка В, вставленная в отверстие в поршне. На втулку кладут перегрузок массой 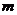. На сколько сместятся втулка и поршень относительно первоначального положения? Плотность жидкости . Площадь сечения сосуда , площадь сечения втулки . Трение отсутствует, зазоры воду не пропускают.

1.7.7*. В дне сосуда сделано круглое отверстие, заткнутое шаром. Радиус шара вдвое больше радиуса отверстия. В сосуд наливают воду. При какой максимальной плотности пробка всплывет. Плотность воды . Указание. Объем шарового сегмента - , 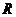- радиус шара, 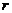- радиус основания сегмента.

Домашнее задание

1. К поплавку массой 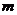привязана леска с большим грузом. При этом поплавок погружен в воду на 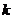-ую часть своего объема. Найти силу натяжения лески, если свободно плавающий поплавок погружен в воду на 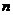-ую часть объема (). Плотность воды .

2. Сосуд, заполненный водой до краев, висит на динамометре. Изменятся ли показания динамометра, если в воду опустить гирю, подвешенную на нити, не касаясь дна? Положить деревянное тело?

3. На весах уравновешен сосуд с водой. В воду опускают тело массой 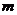, подвешенное на нити. Плотность тела в четыре раза больше плотности воды, оно не касается дна и стенок, вода из сосуда при погружении тела не вливается. Нарушится ли равновесие весов, и если да, то какой дополнительный груз нужно положить на вторую чашку весов, чтобы сохранить их равновесие?

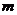4. В цилиндрическом сосуде с водой площадью сечения плавает коробка, в которой лежит кусок свинца. Масса куска свинца , плотность свинца . Понизится уровень воды в сосуде или повысится, если тело вытащить из коробки и переложить в воду? На сколько изменится уровень воды в сосуде? Плотность воды . То же, если тело деревянное.

5*. Система из двух сообщающихся сосудов, один из которых является цилиндрическим, второй имеет форму перевернутого усеченного конуса, заполнена водой. В некоторый момент времени воду в сосуде, имеющем форму конуса нагревают. Как при этом изменится уровень воды в цилиндрическом сосуде?

Статика (2 часа)

План занятия

Определение момента силы. Момент распределенной силы. Центр тяжести тела.

Условия равновесия материальной точки и протяженного тела.

 

Задачи

1.8.1. Стержень массой 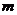и длиной находится в равновесии в горизонтальном положении, опираясь на две опоры. Расстояние от левого конца стержня до левой опоры равно . На вторую опору стержень опирается своим правым концом. Найти силы реакции опор.

1.8.2. Лестница опирается о вертикальную стену и горизонтальный пол. Коэффициент трения между лестницей и полом равен , стена гладкая. Какой минимальный угол может составлять лестница с полом, при котором она находится в равновесии?

1.8.4. Один конец стержня массой 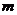прикреплен к вертикальной стенке с помощью шарнира. Ко второму концу стержня приложена некоторая сила , направленная перпендикулярно стержню. В равновесии угол между стержнем и горизонтом равен . Найти силу, с которой стержень действует на ось шарнира.

1.8.5. Плоский прямоугольный треугольник массой 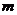с острым углом подвешен шарнирно за вершину угла к горизонтальному потолку. При этом один из катетов треугольника располагается горизонтально. Какой минимальной

силой надо для этого действовать на треугольник?

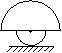1.8.6*. Тело представляет собой два склеенных однородных полушара, центры которых совпадают. Нижний полушар имеет радиус и сделан из материала с плотностью , верхний - радиус и плотность . При каких значениях , , и положение тела, изображенное на рисунке, будет устойчивым?

Домашнее задание

1. Стержень массой и длиной подвешен за концы на двух нитях. К точке стержня, находящейся на расстоянии 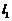от одного из его концов подвешен груз массой 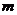. Найти силы натяжения нитей.

2. Находясь на одной чашке неравноплечих, но уравновешенных весов, тело уравновешивается грузом с массой , на другой - . Найти массу тела.

3. Однородный стержень массой 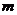расположен на краю стола. За край стола выступает третья часть длины стержня. К выступающему концу стержня подвешен груз. Определить максимальную массу груза, при которой стержень будет в равновесии. Стержень лежит перпендикулярно краю стола.

4. Неоднородное бревно длиной можно уравновесить в горизонтальном положении на подставке, находящейся на расстоянии $l_1$ от его толстого конца. Если подставка находится посередине и на тонкий конец положить груз массой 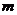, то бревно снова будет в равновесии. Найти массу бревна.

5. Однородный стержень опирается одним концом о шероховатый пол. К другому концу стержня прикреплена нить, расположенная горизонтально. Коэффициент трения между стержнем и полом равен . При каком предельном угле наклона стержня к горизонту возможно такое равновесие?

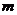6. Колесо с массой и радиусом находится около ступеньки высотой (). Какой минимальной горизонтальной силой необходимо действовать на центр колеса в направлении ступеньки, чтобы оно поднялось на ступеньку?