Основные задачи на построение

С помощью линейки можно провести:

§ произвольную прямую;

§ произвольную прямую, проходящую через данную точку;

§ прямую, проходящую через две данные точки.

С помощью циркуля можно описать из данного центра окружность данного радиуса.

Циркулем можно отложить отрезок на данной прямой от данной точки.

Рассмотрим основные задачи на построение.

Задача 1. Отложить от данного луча угол, равный данному.

Рис.1

Решение. Данный угол с вершиной А и луч ОМ изображены на рисунке 2.

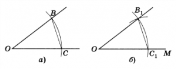Рис.2

Проведем произвольную окружность с центром в вершине А данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис.3, а). Радиусом АВ проведем окружность с центром в точке О — начальной точке данного луча (рис.3, б). Точку пересечения этой окружности с данным лучом обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ABC = Δ ОВ₁С₁ (третий признак равенства треугольников).

Задача 2. Построить биссектрису данного угла (рис.3).

Рис.3

Решение. Из вершины А данного угла, как из центра, проводим окружность произвольного радиуса. Пусть В и С — точки ее пересечения со сторонами угла. Из точек В и С тем же радиусом описываем окружности. Пусть D — точка их пересечения, отличная от А. Луч AD делит угол А пополам. Это следует из равенства Δ ABD = Δ ACD (третий признак равенства треугольников).

Задача 3. Провести серединный перпендикуляр к данному отрезку (рис.4).

Рис.4

Решение. Произвольным, но одинаковым раствором циркуля (большим 1/2 АВ) описываем две дуги с центрами в точках А и В, которые пересекутся между собой в некоторых точках С и D. Прямая CD будет искомым перпендикуляром. Действительно, как видно из построения, каждая из точек С и D одинаково удалена от А и В; следовательно, эти точки должны лежать на серединном перпендикуляре к отрезку АВ.

Задача 4. Разделить данный отрезок пополам. Решается так же, как и задача 4 (см. рис.5).

Рис.5

Задача 5: На за­дан­ном луче от его на­ча­ла от­ло­жить от­ре­зок, рав­ный дан­но­му. От­ре­зок АВ и луч ОС даны по усло­вию:

Рис. 2.1. Усло­вие к при­ме­ру 1

По­стро­е­ние:

Рис. 2.2. Ре­ше­ние к при­ме­ру 1

По­стро­е­ние вы­пол­ня­ем сле­ду­ю­щим об­ра­зом: стро­им окруж­ность с цен­тром в точке О и ра­ди­у­сом АВ. Точка D яв­ля­ет­ся точ­кой пе­ре­се­че­ния окруж­но­сти и луча. От­ре­зок OD – ис­ко­мый, так как он равен АВ.

По­стро­е­ние вы­пол­не­но.

Задача 6. Построить прямую, проходящую через данную точку и параллельную данной прямой

Нам дана прямая а и точка К, не лежащая на прямой а.

Выбираем произвольную точку Т, не лежащую на прямой а и отличную от точки К. Проводим через точку Т перпендикуляр к прямой а (смотри рис), обозначим его прямой b. Через точку К проводим перпендикуляр к прямой b (смотри рис). Построенный перпендикуляр - прямая, параллельная данной прямой.

48. Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой. Грани, отличные от оснований, называются боковыми.
Стороны боковых граней и оснований называются ребрами призмы, концы ребер называются вершинами призмы. Боковыми ребрами называются ребра, не принадлежащие основаниям. Объединение боковых граней называется боковой поверхностью призмы, а объединение всех граней называется полной поверхностью призмы. Высотой призмы называется перпендикуляр, опущенный из точки верхнего основания на плоскость нижнего основания или длина этого перпендикуляра. Прямой призмой называется призма, у которой боковые ребра перпендикулярны плоскостям оснований. Правильной называется прямая призма (Рис.3), в основании которой лежит правильный многоугольник.
Обозначения:
l - боковое ребро;
P - периметр основания;
S_o - площадь основания;
H - высота;
P_^ - периметр перпендикулярного сечения;
S_б - площадь боковой поверхности;
V - объем;
S_п - площадь полной поверхности призмы.

Определение 1. Призматической поверхностью называется фигура, образованная частями нескольких плоскостей, параллельных одной прямой ограниченными теми прямыми, по которым эти плоскости последовательно пересекаются одна с другой*; эти прямые параллельны между собой и называются рёбрами призматической поверхности.
* При этом предполагается, что каждые две последовательные плоскости пересекаются и что последняя плоскость пересекает первую
Определение 2. Перпендикулярным сечением призматической поверхности называется сечение этой поверхности плоскостью, перпендикулярной к её рёбрам. На основании предыдущей теоремы все перпендикулярные сечения одной и той же призматической поверхности будут равными многоугольниками.
Определение 3. Призмой называется многогранник, ограниченный призматической поверхностью и двумя плоскостями, параллельными между собой (но непараллельными рёбрам призматической поверхности)
Грани, лежащие в этих последних плоскостях, называются основаниями призмы; грани, принадлежащие призматической поверхности, - боковыми гранями; рёбра призматической поверхности - боковыми рёбрами призмы. В силу предыдущей теоремы, основания призмы - равные многоугольники. Все боковые грани призмы - параллелограммы; все боковые рёбра равны между собой.
Очевидно, что если дано основание призмы ABCDE и одно из рёбер АА' по величине и по направлению, то можно построить призму, проводя рёбра ВВ', СС',.., равные и параллельные ребру АА'.
Определение 4. Высотой призмы называется расстояние между плоскостями её оснований (НH').
Определение 5. Призма называется прямой, если её основаниями служат перпендикулярные сечения призматической поверхности. В этом случае высотой призмы служит, конечно, её боковое ребро; боковые грани будут прямоугольниками.
Теорема 2. Площадь боковой поверхности призмы равна произведению бокового ребра на периметр перпендикулярного сечения.
Пусть ABCDEA'B'C'D'E' - данная призма и abcde - её перпендикулярное сечение, так что отрезки ab, bc,.. перпендикулярны к её боковым ребрам. Грань АВА'В' является параллелограммом; его площадь равна произведению основания АА' на высоту, которая совпадает с аb; площадь грани ВСВ'С' равна произведению основания ВВ' на высоту bc и т. д. Следовательно, боковая поверхность (т. е. сумма площадей боковых граней) равна произведению бокового ребра, иначе говоря, общей длины отрезков АА', ВВ',.., на сумму ab+bc+cd+de+еа.