Признаками подобия двух треугольников являются такие геометрические признаки, которые позволяют установить, что два неких треугольника являются подобными друг другу, без рассмотрения всех элементов. Теорема 1 Первый признак подобия двух треугольников Треугольники подобны, если хотя бы два угла в неком треугольнике соответственно равны двум углам в другом треугольнике.
Теорема 2 Второй признак подобия треугольников. Треугольники считаются подобными, если две из сторон одного треугольника будут соответственно пропорциональными двум сторонам второго треугольника. Также должно соблюдаться условие равенства углов между этими сторонами.
Теорема 3 Третий признак подобия треугольников. Треугольники считаются подобными, если соблюдается условие пропорциональности трех сторон одного из них трем сторонам второго.
Следствие 1 из теоремы 1. Если рассматривать подобные треугольники, то их сходственные стороны будут пропорциональны высотам, которые будут опущены на сходственные стороны.
Признаки подобия прямоугольных треугольников прямоугольные треугольники считаются подобными, если катет и гипотенуза одного из них пропорциональны катету и гипотенузе второго треугольника; подобными считаются прямоугольные треугольники, если острый угол одного из них равен острому углу второго треугольника.
Квадрат
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
1. Все углы квадрата — прямые, все стороны квадрата — равны.
2. Диагонали квадрата равны и пересекаются под прямым углом.
3. Диагонали квадрата делят его углы пополам.
Площадь квадрата, очевидно, равна квадрату его стороны: 
.
Диагональ квадрата равна произведению его стороны на 
, то есть
.
46. Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
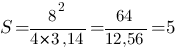
Итого площадь круга будет равна 5 кв. см.